Прямі та площини у просторі

Тема уроку.   Прямі і площини в просторі.

Мета уроку: сформувати уявлення про площину, прос­тір, нескінченність; ознайомити учнів зі способами задання площини, розміщення площин і прямих у просторі.

Освоївши матеріал уроку, учні повинні:

знати:

• способи задання площин;
•  розміщення прямих і площин у просторі;
• основні математичні позначення;
• аксіоми стереометрії;

вміти:

• зображати та знаходити на малюнках прямі і площини;
• застосовувати аксіоми стереометрії до розв’язування задач.

                                           Хід уроку

І. Виклад матеріалу.

Поняття простору і площини

Досі ви вивчали геометрію площини — планімет­рію. Сьогодні ми ознайомимося з геометрією про­стору — стереометрією. Так само, як і планіметрія, стереометрія оперує поняттями: точка, відрізок, промінь, пряма, та додається нове поняття — «пло­щина». Щоб створити образ цього поняття, уявімо рух точки, прямої і площини.

Точка рухається в одному напрямі, образом її руху є... (учні відповідають — пряма).

Горизонтальна пряма рухається, скажімо, верти­кально. Образом її руху стане... (площина, — відпові­дають учні).

Площина рухається і заповнює простір.

Зауважимо, що пряма, площина, простір не­скінченні. Розуміння нескінченності у математиці, фізиці, історії різне.

Математики мислять масштабно: нескінченність це дуже багато і далеко. Фізики можуть вважати не­скінченно великим навіть відрізок завдовжки в один сантиметр, залежно від того, чим вимірювати. Якщо, наприклад, атомами, електронами, протонами.

А якщо вимірювати час: сьогодні, завтра, учора, зараз, цієї хвилини, цієї секунди? Навіть найваж­ливіші події з часом стають історією. А коли? Ми спостерігаємо за подіями «із зовні», «з нескінчен­ності кроків». Велике бачиться на відстані, віч-на-віч обличчя не побачити. Але щоб оцінити важливість події, потрібно віддалитися від неї на нескінченно багато миттєвостей, пережити й набути досвіду. У кожного ці миттєвості свої, але світ єдиний, відрізня­ються лише точки зору на нього. Наочно уявити не­скінченність допоможе гравюра Ешера.

   Ми живемо в просторі, в тривимірному світі. Площина допомагає людині сприймати світ, роз­глядати його. Планіметрія це завдання виконувала протягом багатьох століть. Площина потрібна для того, щоб зосередити думки, зупинити мить. Цим прийомом користуються і художники. Перед вами репродукція картини В.І.Сурикова „Бояриня Моро­зова”.

Картина розтягнута в ширину, ніби підкреслює масштабність події. На триптиху П.Д.Коріна «Олек­сандр Невський» постать у цен­тральній частині витягнута, зібрана, натягнута як струна. Відразу сприймаєш велич духу     людини. Прикладів застосування математичних понять у різних галузях знань багато. Наприк­лад, уявлювані площини в хімії допомогли створити теорію   ізомерів. А в природі кожен листок, перебуваючи у  своїй      площині, повертається до Сонця,  і планета дихає.

Можна навести ще багато прикладів, але ви вже зрозумі­ли, що з  площинами ми зустрі­чаємося щодня. Моделлю пло­щини може бути, скажімо, по­верхня учнівського стола.

Пригадаємо, як можуть розміщатися прямі на площині. (Учні відповідають.)

Правильно, прямі можуть перетинатися і не пе­ретинатися. Як же можна задати площину? (Учні відповідають.)

 Підбиваємо підсумок. Площину можна задати: трьома точками, що не лежать на одній прямій, па­ралельними прямими, прямими, що перетинаються, прямою і точкою, що не лежить на цій прямій.

А зараз перевіримо ваше уміння бачити і спосте­рігати.

   • Перед вами фотографія пам'ятника Петру І в Санкт-Петербурзі. Чому кінь не падає? Адже він стоїть на двох но­гах!?

• Коли три мухи, які летять, будуть в одній пло­щині?

• Чому табурет на трьох ніжках більш стійкий, ніж табурет на чотирьох ніжках?

 

 

 

 

Розміщення площин і прямих у просторі.

Площини називаються паралельними, якщо вони не мають спільних точок. Запис: .

Площини перетинаються, якщо вони мають хоча б одну спільну точку. Площини перетинаються по прямій. Запис: .

Паралельні площини і площини, що перетина­ються, утворюють видимий об'єм наших приміщень. Ви не помічали, що площина стелі, пофарбована білим, робить кімнату вище? А якщо стіни зробити червоними, то в людини підвищується рівень адре­наліну в крові. А жовтий і зелений кольори заспо­коюють.

У просторі, так само, як і на площині, пряма за­дається двома точками. Прямі можуть бути паралель­ними або перетинатися, тоді вони лежать в одній площині.

Прямі в просторі, які лежать у різних площинах, та не паралельні і не перетинаються, називаються мимобіжними.

                                       Розміщення прямої і площини.

Пряма і площина можуть перетинатися. Запис: .

Пряма може бути паралельною площині. Запис: . У цьому випадку пряма і площина спільних точок не мають.

Пряма, яка перетинає площину, перпендикуляр­на до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині, і прохо­дить через точку перетину. Запис: .

Відстанню від точки до площини називається дов­жина перпендикуляра, проведеного з цієї точки до площини.

Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпен­дикулярна до прямої перетину даних площин, пере­тинає їх по перпендикулярних прямих.

 

II. Закріплення матеріалу.

                                         Задачі на розглядання

Задача 1. Назвіть (рис. 1):

1. точку перетину прямої АD і площини DD₁C;
2. лінію перетину площин АDD₁  і DD₁С;
3. в яких площинах лежить точка В;
4. три прямі, що проходять через точку D, пере­тинають четверту в точках А, В, С.

 

 

 

 

 

Рис. 1 Рис. 2

Доведіть, що точки А, В, С і D   лежать в одній площині.

Задача 2 (рис. 2). Назвіть:

1. точку перетину прямої BD  і площини АВС;
2. лінію перетину площини АВD і СВD;
3. в якій площині не лежить точка С.

Прямі АВ і  АС перетинаються з деякою прямою в точках К і М відповідно. Доведіть, що М, К, С, і В лежать в одній площині.

Задача 3. Назвіть (рис. 3):

1. точку перетину прямої МС і площини ВВ₁С;
2. лінію перетину площин МС₁С і ВСВ₁;
3. в яких площинах лежить пряма МD.

Доведіть, що точки А, В, С і D лежать в одній площині.

Задача 4. Побудуйте лінію перетину (рис. 4):

1. площини АВС і прямої МК;
2. площини МКВ і АВ.

 

 

 

 

 

Рис. 3 Рис. 4 Рис. 5

Задача 5. Чи лежить точка К  в площині паралелограма АВСD, якщо N належить прямій AD, а М належить прямій ВС (рис. 5)?

Задачі на уяву

1. Чи можуть дві різні площини мати три спільні точки, що не лежать на одній прямій?

2. Чи можуть дві різні площини перетинатися по двом прямим?

3. Прямі а, b, c не належать одній площині, але проходять через одну точку. Скільки різних площин можна провести через ці прямі, взяті по дві?

4. Площини перетинаються по прямій а. Пряма b, що лежить у площині,  перетинає площину в точці А. Де лежить точка А?

5. Точка А і В та пряма СD не лежать в одній площині. Яке взаємне розміщення прямих CD i AB?

                Завдання на розуміння мови математичних символів

1. Дано вирази

 

1. Серед цих виразів знайдіть помилкові.
2. Який із записів відповідає висловленню:

а) площини перетинаються по прямій а;

б) точка А є точкою перетину площини   і прямої а?

2. Як можуть розміщатися прямі а та АВ у площинах і ? Запишіть мовою символів.

ІІІ. Домашнє завдання.

Вивчити опорний конспект, розв’язати задачі.

Запишіть висловлення мовою символів:

1. точка А перетинає площину 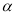  в точці В;
2. прямі КА і КВ перетинаються в точці К;
3. пряма КН перпендикулярна до прямої МС. На перетині прямих лежить точка К.

Тестові завдання

1.   а) Дано куб АВСДА₁В₁С₁Д₁. яка з точок не лежить у площині квадрата АВСД?

1) М; 2) К; 3) N; 4) Р.

б) Дано тетраедр АВСS. Яка з точок не лежить у площині трикутника АВС?

1) А; 2) Z; 3) Y; 4) X.

 

 

 

 

2.  а) Якій із вказаних площин куба не належить точка А?

 1) ВСД; 2) А₁С₁С; 3) ВВ₁А₁; 4) ВСС₁.

б) Якій із вказаних площин тетраедра належить точка У?

1) ASB; 2) ASC; 3) BSC; 4) ZBC.

 

 

 

 

3. У просторі дано прямі а та в, які перетинають­ся в точці С. Скільки різних площин можна провес­ти через ці прямі?

1) дві;     2) безліч;    3) одну;      4) жодної.

4. а) Площини тетраедра АSС і АSВ перетинаються по прямій:

 1) AS; 2) AB; 3) AC; 4) SC.

б) Площини куба АВС і В₁ВД перетинаються по прямій:

 1) ВС; 2) ВД; 3) АВ; 4) ВВ₁.

 

 

1. а) Площину ABS тетраедра можна задати прямими:

1) АВ і АS;  2) АВ і АС; 3) АС і ВС.

б) Площину грані АА₁Д₁Д куба АВСДА₁В₁С₁Д₁ можна задати прямими:

1) Д₁Д і ДС; 2) АД і АВ; 3) АА₁ і АД; 4) А₁Д₁ і Д₁С₁.