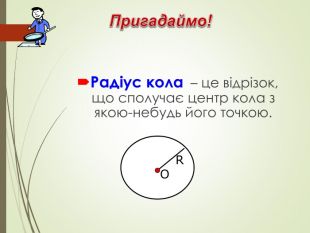
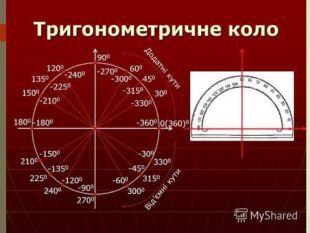
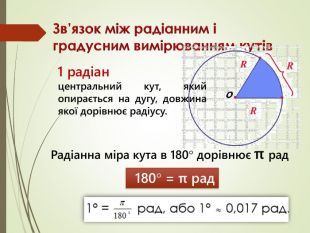
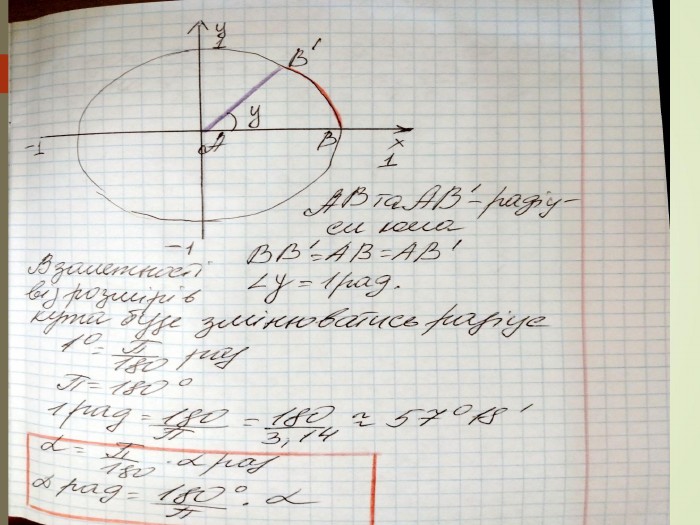
Радіанне вимірювання кутів


























МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ М.П.ДРАГОМАНОВА ФАКУЛЬТЕТ МАТЕМАТИКИ, ІНФОРМАТИКИ ТА ФІЗИКИ Заочне відділення Завдання 2 Тема « Введення радіанної міри кута. Задачі на засвоєння. » Виконала: студентка 1 курсу групи 1ммзСО Мігульова Ольга Викладач Лук»янова С.М
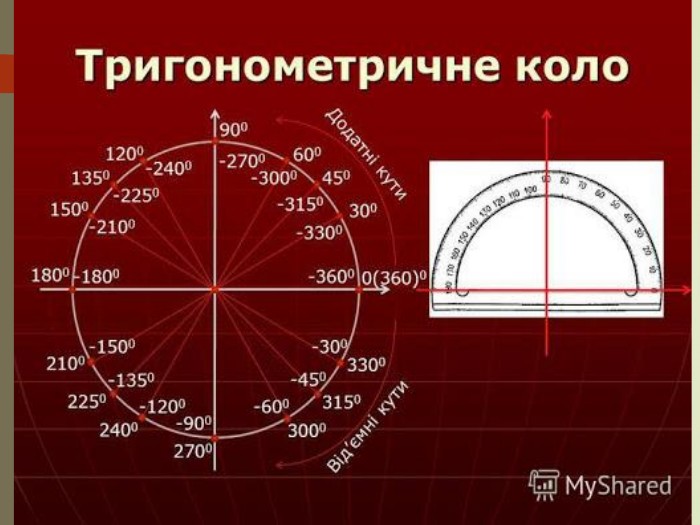
План вивчення теми 1.Що таке один радіан? 2.Кут повороту. 3.Додатні і від’ємні значення кутів повороту. 4.Перехід від градусної міри кута до радіанної. 5. Перехід від радіанної міри кута до градусної. 6.Задачі на закріплення 7. Системи вимірювання кутів в різних галузях 1.Що таке один радіан? 2.Кут повороту. 3.Додатні і від’ємні значення кутів повороту. 4.Перехід від градусної міри кута до радіанної. 5. Перехід від радіанної міри кута д градусної. 6. Одиничне коло . Поворот точки навколо початку координат.
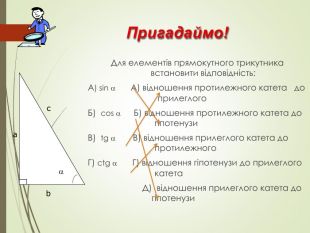
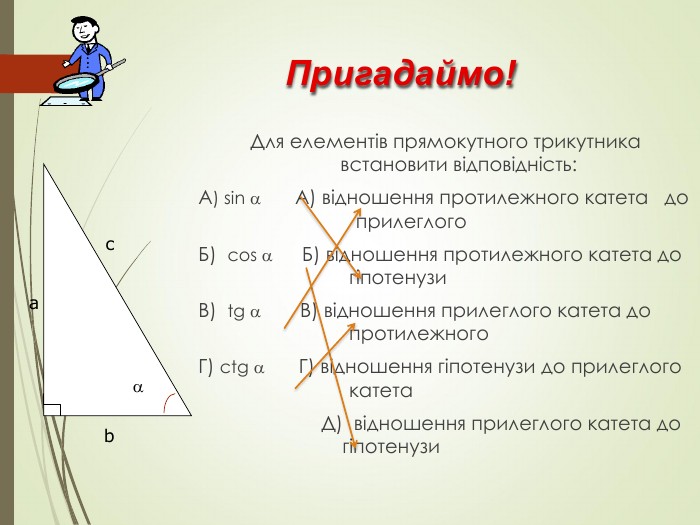
Пригадаймо! Для елементів прямокутного трикутника встановити відповідність: А) sin А) відношення протилежного катета до прилеглого Б) cos Б) відношення протилежного катета до гіпотенузи В) tg В) відношення прилеглого катета до протилежного Г) ctg Г) відношення гіпотенузи до прилеглого катета Д) відношення прилеглого катета до гіпотенузи с b a
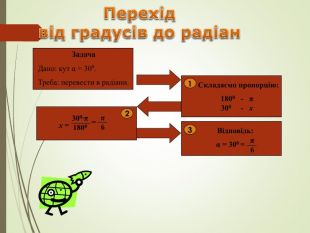
Пригадаймо! Градусна міра кута Ще в Древньому Вавілоні за довго до нашої ери жреці вважали, що свій денний шлях сонце проходить за 180 кроків, а значить один крок складає 1/180 розгорнутого кута. У Вавілоні була прийнята шести десятирічна система числення, тобто фактично числа записувались у вигляді суми степенів числа 60, а не 10. Тому зрозуміло, що для більш мілких одиниць вимірювання кутів один “крок ” послідовно ділиться на 60 частин. А саме слово “градус” походить від латинського gradus (крок, сходинка). Секунда перекладається як “друга”.
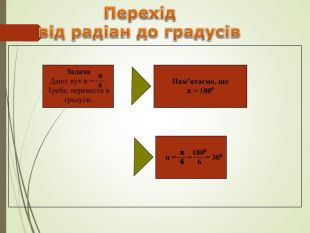
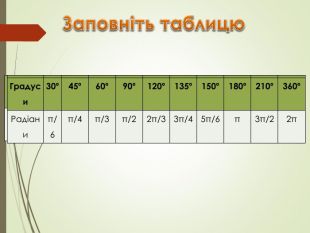
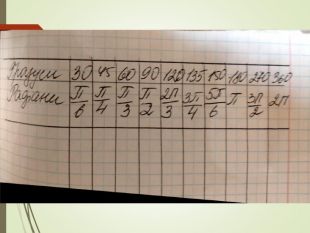
Градуси Радіани π/3 2π/3 5π/6 3π/2 Градуси Радіани π/6 Градуси Радіани π/6 π/4 Градуси Радіани π/6 π/4 π/3 Градуси Радіани π/6 π/4 π/3 π/2 Градуси Радіани π/6 π/4 π/3 π/2 2π/3 Градуси Радіани π/6 π/4 π/3 π/2 2π/3 3π/4 Градуси Радіани π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 Градуси Радіани π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π Градуси Радіани π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 Градуси Радіани π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π


про публікацію авторської розробки
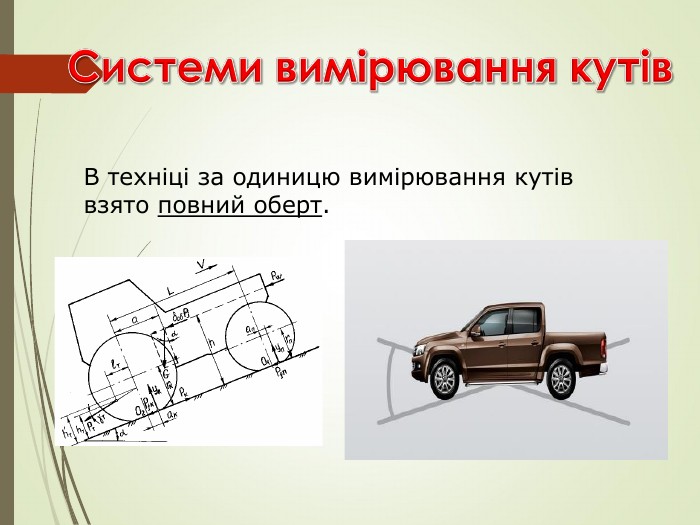
Додати розробку