Радіанне вимірювання кутів

Тема уроку: Радіанне вимірювання кутів

Мета уроку:ввести поняття радіанного вимірювання кутів; пояснити механізм переведення кутів із радіанної міри в градусну і навпаки; формувати вміння переходити від однієї міри вимірювання кутів до іншої

Тип уроку: засвоєння нових знань.

Хід уроку

І. ОРГАНІЗАЦІЙНИЙ ЕТАП

ІІ ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 Завдання середнього рівня учні коментують з місця,  завдання достатнього і високого рівнів можна перевіряти, запропонувавши учням виконати аналогічні завдання на дошці.

 Завдання класу

1 Знайдіть такий кут α, 0 ≤α ≤ 360º , щоб поворот початкового радіуса на цей кут збігався з поворотом на кут: а) 530°;              б) -460° .

2. Укажіть найбільше і найменше значення виразу, а) 1-sin α; б) 2 + cos α.

3. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

 Запитання до класу

1.    Запишіть формулу довжини кола. Обчисліть її при R=2см.
2.    Запишіть формулу довжини дуги в п°. Знайдіть довжину п дуги при п = 60°
3.    Якими співвідношеннями пов’язані між собою градуси, хвилини, секунди?

4. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ І ЗАВДАНЬ УРОКУ;

МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Як відомо, кути вимірюються в градусах, хвилинах, секундах. При вимірюванні кутів у градусах за одиницю вимірювання приймається кут, який дорівнює — частини розгорнутого кути. Його називають градусом.

Однак у фізиці, техніці, астрономії часто можна зустріти й іншу міру вимірювання кутів, що має певні переваги перед іншими системами.

5. СПРИЙНЯТТЯ Й ОСМИСЛЕННЯ НОВОГО МАТЕРІАЛУ

1. Учитель формулює означення кута в 1 радіан (рис. 1).
2.  
   
   
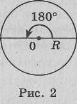
   Установлюється зв’язок між радіанним і градусним вимірюванням кутів (рис. 2).

πR — довжина півкола. 180° =0°. Звідси

Зауваження. Величина кута, виражена в радіанах, не зале­жить від довжини радіуса.

У записі радіанної міри кута позначення «рад» часто опу­скають.

3. Перевага радіанної міри кута полягає в тому, що геометричні формули довжини дуги й площі сектора спрощуються і мають вигляд l = Ra, S =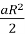, де R — радіус кола, а — радіанна міра дуги.

Радіанна міра дає можливість увести поняття тригонометрич­ної функції довільного числового аргументу.

VI ПЕРВИННЕ ЗАКРІПЛЕННЯ НОВОГО МАТЕРІАЛУ

1. Знайдіть градусну міру кута, радіанна міра якого дорівнює:

2.  Знайдіть радіанну міру кута, який дорівнює:

а) 120°;  6)150°;  в) 36°;  г) 300°;  д)-225°.

3. Кутом якої чверті є кут а, якщо:

а) α = ; б)α = 1,2π?

4

4.  Обчисліть:

a) sin² - sin²; б) 2sin - 3tg + ctg

VІІ. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

Заповніть таблицю, використовуючи отримані на уроці формули.

VIІІ. ДОМАШНЄ ЗАВДАННЯ

1.    Виразіть у радіанній мірі величину кута:

а) -150°; б) 240°; в) 100°.

2.    Виразіть у градусній мірі величину кута:

а) 3π; б) в)  г)3.

3.    Кутом якої чверті є кут а, якщо:

а) α = ;; б) α = -2,1π; в) α = 1?