Реферат на тему: «Логарифми. Логарифмічна функція»

 

 

 

 

Реферат на тему: «Логарифми. Логарифмічна функція»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст 

1. Короткі відомості з історії логарифмів.
2. Визначення логарифма, десяткові та натуральні логарифми.
3. Основна логарифмічна тотожність.
4. Логарифмічна функція та її властивості.
5. Формула переходу від 1 основи логарифма до іншої.
6. Приклади розв’язування завдань.
7. Висновок.
8. Список використаних джерел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Короткі відомості з історії

    Англійський математик Дж. Непер (1550-1617) швейцарський математик І. Бюргі (1552-1632) незалежно один від одного ввели логарифми.

   Теорію логарифмів розвинув Непер. Він розробив способи обчислення арифметичних виразів за допомогою логарифмів і склав детальні таблиці логарифмів. Таблиці Непера мало відрізнялись від сучасних таблиць натуральних логарифмів.

   Десяткові логарифми ввів англійський математик І. Брігс (1561-1630). Лейбніц ще в кінці XVII ст. за допомогою правил логарифмування розв'язував показникові рівняння. Використання таблиць логарифмів, а пізніше - логарифмічної лінійки значно спростило обчислення, і вони довго були одним з основних засобів обчислень.

   Французький математик Лаплас говорив навіть, що винайдення логарифмів подовжило життя обчислювачів.

 

       Дж. Непер І. Бюргі

 

 

 

 

 

 

 

Поняття логарифмічної функції

 Розглянемо показникову функцію та знайдемо формулу оберненої до неї функції.

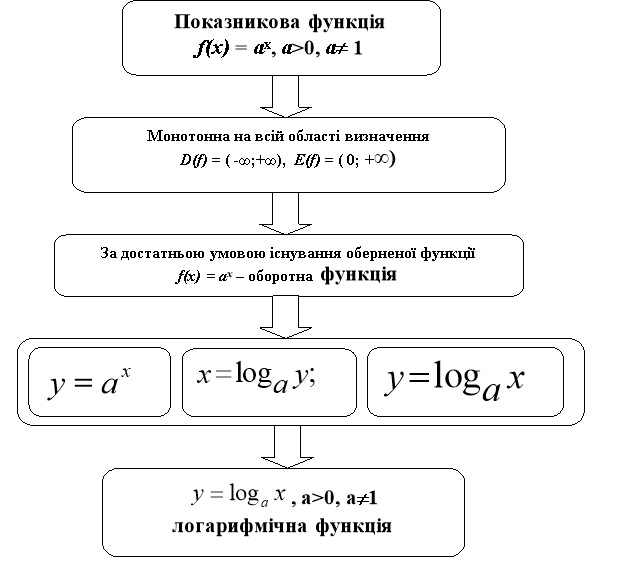
 Логарифмічною називається функція , де a>0, a1, обернена до показникової у=а^х.

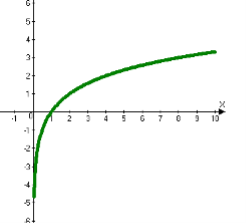
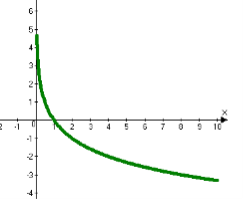
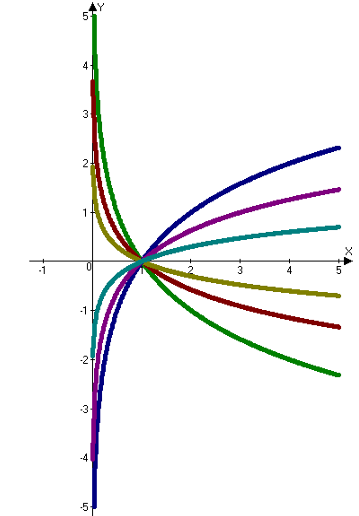
2. Графік логарифмічної функції.(Міні-дослідження)

 Для побудови графіка логарифмічної функції та формулювання її властивостей, я пропоную вам виконати таке завдання:

І група Побудувати графік функції .

ІІ група Побудувати графік функції .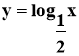

 

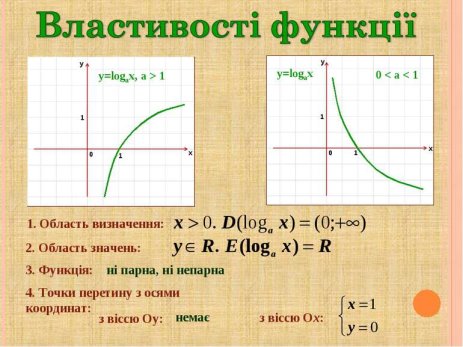
 Властивості логарифмічної функції.

 Властивості функції записані учнями кожної групи на плакаті. Аналізуємо властивості логарифмічної функції (в загальному вигляді), записуємо їх у зошит.

Щоб відповісти на ці питання, скористаємось графіками.

 

 

 

 

 

 

 

 

          

          

          

 

 

 

          

          

          

 

 

 

 

 

 

 

 

 

 

Властивості логарифмічної функції	, a>1	, 0<a<1
Графік
1. Область визначення функції	D(f) = ( 0; +∞)
2. Область значень функції	E(f) = ( -∞;+∞)
3. Парність, непарність.	Функція не є ні парною, ні непарною (функція загального вигляду).
4. Перетин з осями координат	Якщо х=1, то у=0, тобто графік проходить через точку (1;0)
6.Монотонність	Монотонно зростає на  R	Монотонно спадає на R

 

Визначення логарифма, десяткові та натуральні логарифми

  Розглянемо рівність 4? = 64. У цій рівності число 3 є показником степеня, до якого необхідно піднести число 4, щоб дістати 64.   Аналогічно, в рівності число (-2) є показником степеня, до якого треба піднести 5, щоб дістати .

 Логарифмом числа N за основою а (а > 0, а ? 1) називається показник степеня х, до якого треба піднести основу а, щоб дістати число N.

Саме слово „логарифм” замінюють символом log, праворуч біля якого (у нижньому регістрі) записують число, яке називають основою, наприклад log₃81.

У багатьох випадках зручно використовувати десяткові логарифми, тобто логарифми за основою 10, для запису яких застосовують символ lg (без нижнього регістру), наприклад lg10 = 1, lg100 = 2. 

Перш ніж ввести поняття натурального логарифма, слід ознайомити читача з унікальним числом, яке називають числом Ейлера і позначають е.

Число е виникло при вивченні виразів типу . У курсах вищої математики доведено, що даний вираз монотонно зростає. За ознакою Веєрштраса вираз має границю, яка дорівнює … Дане ірраціональне число (доведення його ірраціональності виходить за межі не лише цього реферату, а й шкільного курсу) називають числом Ейлера і позначають, як я вже зазначала, літерою е. Унікальність, або, як нині модно говорити, „магію” цього числа можна помітити, досліджуючи показникову функцію y = а^x, Факт, що лише при а = е кутовий коефіцієнт дотичної до графіка функції y = а^x у точці x = 0 рівний одиниці (дотична утворює кут 45° з віссю абсцис).

Крім того, швидкість зміни функції y = е^x в кожній точці дорівнює значенню цієї функції в цій точці. Всі інші похідні цієї функції (їх безліч) також рівні е^x. Первісна від функції y = е^x рівна самій цій функції. Згадана функція єдина, що має вказані властивості.

 По експоненціальному закону проходять дуже багато природних і штучних процесів, насамперед ріст деревини, охолодження рідин, майже всі процеси в термодинаміці, радіоактивний розпад.

 Натуральним логарифмом називають логарифм за основою е (позначають ln x). Цікаво, що саме через натуральні логарифми виражені переважна більшість інтегралів від елементарних і неелементарних функцій.

Основна логарифмічна тотожність

 Розглянемо показникову рівність а^х = N.

За означенням логарифма x = lоg_аN 

Замінюючи в рівності x його значенням з рівності x = lоg_аN. 

Рівність називають основною логарифмічною тотожністю.

Логарифмічна функція та її властивості

 Варто дати означення логарифмічній функції за основою а (а > 0, а ? 1). При а > 1 показникова функція зростає на всій числовій прямій, а при 0 < а < 1 спадає на всій числовій прямій, при цьому в обох випадках Е (а^x) = R₊. За теоремою про обернену функцію показникова функція y = а^x має обернену функцію з областю визначення R₊ і множиною значень R, яка неперервна в кожній точці області визначення. Цю обернену функцію називають логарифмічною функцією за основою а і позначають у = lоg_а. З тої ж теореми випливає, що при а > 1 функція lоg_а зростає, а при 0 < а < 1 спадає на множині R₊.

1. 

Логарифмічна тотожность

 

Формула переходу від 1 основи логарифма до іншої

 

 

 

 

 

 

 

 

Приклади розв’язування завдань

 

 

Логарифмічні нерівності

Розв’язуючи логарифмічні нерівності, доцільно використати загальну схему рівносильних перетворень нерівностей. Ця схема іноді дає надмірну систему обмежень, яку можна суттєво спростити. Для рівносильності рівнянь надмірність системи обмежень майже не впливає на об’єм роботи щодо розв’язування цих рівнянь - можна не знаходити відповідні значення змінної з цих обмежень, а тільки перевіряти для кожного знайденого кореня. Розв’язком нерівності, як правило, є інтервал (або кілька інтервалів), які містять нескінчену множину чисел, а всі їх перевірити неможливо. Отже для розв’язування нерівності доведеться знаходити відповідні значення змінної з усіх записаних обмежень, і тому чим менше залишиться цих обмежень, тим краще. Бажано запропонувати учням не знаходити окремо область визначення нерівності, а спочатку записувати повну систему обмежень і рівносильну нерівність, а потім намагатися споростити утворену систему.

 

 

 

 

Застосування логарифмів та логарифмічної функції в науці, техніці та природі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТКИ

 

 

Застосування логарифмів та логарифмічної функції

 

Математика

 

Логарифм – з грецької  означає “логос”- відношення і “аритмос”-  число. 

Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і тяжких обчислень, відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не отримали широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число e неперовим числом.

Ідея десяткових логарифмів виникла у професора лондонського коледжу Генрі Брігса(1561-1630) після ознайомлення з таблицями Непера. Він двічі побував у Непера, здружився з ним і в процесі спільних занять обидва розробили нову, практично зручнішу десяткову систему, засновану на порівнянні прогресії.

 Брігс взявся розробити велику таблицю десяткових логарифмів. Уже в 1617 р. він опублікував восьмизначні таблиці логарифмів від 1 до 10³, а в 1624 році спромігся  видати «Логарифмічну арифметику», що містила чотирнадцятизначні таблиці логарифмів для чисел 1-20000 і 90000-100000.

Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас (1749-1827), продовжуючи життя обчислювачам.

Ще донедавна важко було уявити собі інженера без логарифмічної лінійки в кишені. Винайдена в 1624 році англійським математиком Едмундом Гунтером (1581-1626), вона дозволяла швидко одержувати відповідь з достатньою для інженера точністю до трьох значущих цифр. І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було і перших комп’ютерів.

 

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.

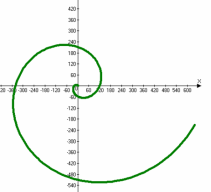 Рівняння (в полярних координатах) має вигляд: .

 

 

 Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.

Характерні особливості логарифмічної спіралі:  

• Має нескінченну кількість витків як при розкручуванні так і при скручуванні;
• Не проходить через свій полюс;
• Її називають рівнокутною спіраллю;
• В будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає               постійне значення;
• При різних перетвореннях (гомотетії, повороті) вона залишається незмінною.
• Має широке застосування в технічних приладах.
• Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

 

ФІЗИКА

 

Фізика  завжди вимагає математичних розрахунків, тому знання математики у фізиці завжди необхідне. Ось декілька формул, де використовуються логарифми.

 

• Робота, яку виконує газ при ізотермічному процесі

  

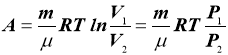
m – маса газу;

µ - молярна маса газу;

R – універсальна газова стала;

Т  – температура за Кельвіном;

V -  об’єм газу;

P – тиск газу.

• ємність циліндричного конденсатора:

  

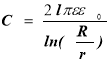
L – висота циліндра;

R, r – радіуси внутрішнього та зовнішнього циліндра;

 – техн. характеристики конденсатора;

• Ємність дільниці одиничної довжини двох провідної лінії

  

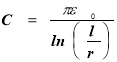
   r – радіус провідника

• Зв’язок між сталою розпаду, середнім часом життя і періодом піврозпаду Т

  

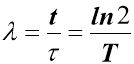
    – середній час життя;

   Т – період піврозпаду;

• Рівень інтенсивності звуку

  

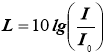
  - умовно нульовий рівень

• Ентропія

  S=kln

К – стала Больцмана;

Ω - термодинамічна імовірність ;

S – ентропія;  

 

• Зміна ентропії при ізотермічному стисканні газу

  

R – універсальна газова стала

µ - молярна маса газу

m – маса газу;

V – об’єм газу

 У техніці часто застосовуються ножі, що обертаються. Сила, з якою вони тиснуть на матеріал, що розрізається, залежить від кута розрізання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того, щоб тиск був сталим, потрібно щоб залишався сталим кут розрізання, а це буде у  тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Завдяки цьому лезо ножа сточується рівномірно.

 Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

 

 У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

 

Хімія

 

 Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну,що характеризується різною концентрацією йонів Гідрогену С( Н⁺).Для зручності датським біохіміком С.Сьоренсеном у 1909 році було введено термін «водневий показник» (рН), –це значно спростило роботу багатьом поколінням хіміків.

 Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену

рН= - lg С( Н⁺)

 Значення рН може змінюватись від 1 до 14

Наприклад, С( Н⁺)=10^-7,рН=7;

  С( Н⁺)=10^-2 ,рН=2.

У нейтральному – рН=7.

У кислому середовищі рН<7, у лужному рН>7,

Показник рН в біологічних розчинах

Рідина	рН	Рідина	рН
Шлунковий сік	1,4	Сеча	6,0
Сік лимона	2,1	Слина,молоко	7,4-8
Сік яблук "Антонівка"	2,5	Слюзи	7,0
Томатний сік	4,1	Кров	7,4

 З таблиці видно, що різні розчини в людському організмі мають різний рН, його відхилення від норми спричиняє захворювання і навіть загибель організму. Людям з підвищеною кислотністю шлункового соку рекомендується пити мінеральну воду з меншою концентрацією йонів Н⁺ (тобто з вищим рН),а зі зниженою кислотністю - "кислішу" воду(з нижчим рН).

 Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5. Відповідний вміст у них катіонів Н⁺ оптимальний для нашої шкіри.

   

 У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7).

 

БІОЛОГІЯ

 

 Можна сказати, що спіраль є математичним символом співвідношення форми і зростання.

 Великий німецький поет Йоганн-Вольфганг Гете вважав її символом життя і духовного розвитку.

 Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

       

 

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

 

 

МУЗИКА

 

 Розкопуючи одне з поселень кам’яного віку на території України, археологи знайшли кілька кісток мамонта, призначення яких було їм не зрозуміле. Лише уважний аналіз показав, що на цих кістках залишилися сліди ударів - це були залишки шумового оркестру, під звуки якого стародавні люди виконували магічні танці. Пізніше помітили, що більш приємні звуки можна отримати, зробивши барабан або просвердливши шматок дерева, щоб вийшла сопілка. А звучання тятиви лука? Воно навело на думку про створення струнних інструментів.

 Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.

 Будемо називати найнижчу октаву нульовою; а кількість коливань ноти do цієї октави за 1 секунду приймаємо за 1.Тоді нота do першої октави буде робити в два рази більше коливань. Позначимо всі ноти хроматичної гами номерами р , приймаючи за нульовий перший тон кожної гами. Тоді тон sol буде 7-й, la -9-й, 12-й тон буде знову do, тільки октавою вище.

 Тому кожен наступний тон в разів має більше коливань, ніж попередній.

 Позначимо Npm – кількість коливань тону з номером р із m-ї октави.

Nmp=2 ( )=2·2= 2+

 Про логарифмуємо обидві частини останньої нерівності:

logNmp= m+

 Звідси видно, що номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок

    Отже, знаючи всі логарифмічні властивості,можна сміливо розв’язувати завдання з логарифмами.   Основна схема для розв’язування.

1. Уявити основу a і число x у вигляді степеня з мінімально можливою основою, більше одиниці.

2.Водночас краще позбутися десяткових дробів;

3.Вирішити відносно змінної b рівняння: x = ab. Отримане число b буде відповіддю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

 

1.  Сайт Вікіпедія  

2. М. І. Шкіль, З. І. Слепкань, О. С. Дубинчук - Алгебра і початки аналізу. Підручник для 10 класу середньої школи. К.: „Зодіак-Еко”, 2001.

3. А. М. Колмогоров - Алгебра і початки аналізу. Підручник для 10 класу середньої школи. К.: ”Радянська школа”, 1977.