"Рівні множини. Число елементів множини. Порожня множина.»

Урок 3

Тип урока: ОНЗ.

Тема: «Равные  множества. Число элементов множества. Пустое множество.»

Основные цели:

1) формировать способность к установлению равенства множеств, к приобретению знаний о количестве  элементов в  множестве, познакомить с понятием пустого множества и его обозначением;

2) повторить  приёмы устных и письменных вычислений, решение текстовых задач на  разностное и кратное сравнение, составление буквенных выражений к текстовым задачам.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, классификация.

Демонстрационный материал:   

1) Карточка с девизом урока: «ГДЕ ЕСТЬ ЖЕЛАНИЕ – НАЙДЁТСЯ ПУТЬ!»

2) Эталон сравнения групп предметов  Э – 1 .

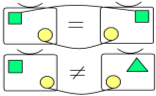ДВЕ ГРУППЫ РАВНЫ, ЕСЛИ ОНИ СОСТОЯТ ИЗ ОДНИХ И ТЕХ ЖЕ ПРЕДМЕТОВ.

 

 

 

 

 

3) эталон способов задания множеств  Э – 2:

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ           А = {1, 2, 3,…9}                                                         А ― множество однозначных чисел Помни: Элементы множества не могут повторяться!

 

4)  свойства множеств  Э – 3:

     *  элементы собраны вместе

     *   элементы не повторяются

     *   порядок расположения элементов неважен  

5)  Эталон сложения двузначных чисел с переходом через десяток ( частный случай ) 

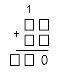Э- 4:

 

 

 

 

6)  карточки с шагами плана:

      ПЛАН:

     1. Записать множества А  и  В.

     2. Каждому элементу множества А соотнести элемент множества В.

     3. Проанализировать.

     4. Сделать вывод . 

7) эталон «Равные множества»   Э – 5  .

Равные множества - это множества, которые состоят из одних и тех же элементов  (порядок записи элементов не имеет значения)

 

 

8) эталон пустого множества Э – 6

Множество, не содержащее ни одного элемента, называется пустым.

{         } =

 

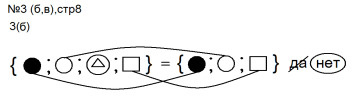
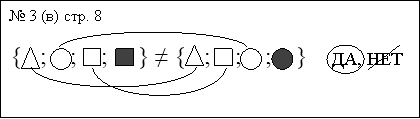
9) образец для работы в парах: № 3 (б, в).

 

 

 

 

 

 

 

 

 

 

 

 

 

10) эталон для самопроверки к самостоятельной работе № 4 , стр. 8; № 6 (а), стр. 8.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

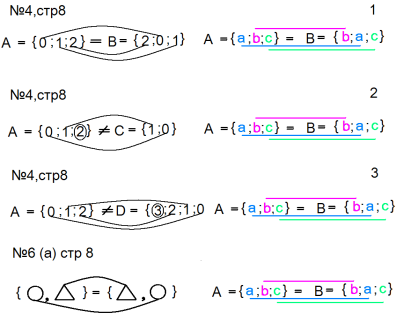
11.  эталон для решения текстовых задач  на  разностное и кратное сравнение

( для этапа 8):

 

 

 

 

 

 

 

 

 

 

 

 

 

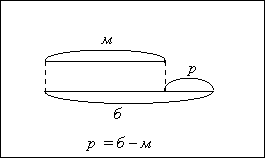
12)  заготовки схем  к решению  текстовых задач на этапе 8 (№ 11 , стр. 9 ) .

 

 

 

 

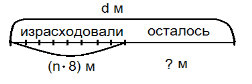
Раздаточный материал.

1) планшеты;

2) индивидуальное задание для 2 этапа:   

 Дано  множество А, заданное общим свойством элементов – множество осенних месяцев --  и множество  В, заданное перечислением элементов  --

В = {сентябрь; октябрь; ноябрь; декабрь}

В течение 1 минуты запишите  эти множества и  обведите правильное (на ваш взгляд) утверждение:

        А  равно  В                              А  не равно  В

3) правила работы в группе (см. урок №  2 , М-3 , ч-1 , Р-2);

4) набор треугольников зелёного, жёлтого и красного цвета (см. урок -1 , М-3 , ч-1) .

 

Ход урока:

1. Самоопределение  (мотивация) к учебной деятельности.

Цель:

1. создать мотивацию к учебной деятельности путём предъявления девиза и эмоционального диалога;
2. определить содержательные рамки урока:  расширение темы множества;
3. включение учащихся в учебную деятельность – тренировать в понимании значения шагов учебной деятельности.

Организация учебного процесса на этапе 1:

-Ребята, какой теме был посвящён прошлый урок? (теме «множества», способам задания множеств)

-Правильно. На самом деле тема «множества» очень объёмная, большая, в ней ещё много незнакомой нам информации. Чем, по вашему мнению, мы будем заниматься сегодня?

( узнавать что-то новое  по теме «множества »)

-Вы снова правы!

-Что значит «узнавать новое»? Скажите конкретнее. (Мы должны понять « чего мы не знаем » и «сами найти способ» узнать это новое)

-Тогда давай возьмём в качестве девиза урока такое утверждение:

                         ГДЕ ЕСТЬ ЖЕЛАНИЕ – НАЙДЁТСЯ ПУТЬ!  (на доске карточка Д – 1)

-У вас есть желание добывать новые знания? (да)

-Тогда в путь-дорогу.  Я желаю вам успеха!

 

2.  Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1) актуализировать представления о сравнении групп предметов, о способах                         задания множеств, основные свойства множеств;

2) тренировать мыслительные операции – анализ, сравнение, обобщение,    классификацию – на примере множества, заданного в виде закономерности;  приемов устных  и письменных  вычислений;

3)     организовать  фиксацию актуализированных способов действий в эталонах

 и вербально;

 4)  мотивировать к пробному действию, организовать его самостоятельное            выполнение  и обоснование;

 5)  организовать анализ полученных ответов и зафиксировать индивидуальное    затруднение в выполнении пробного задания или его обосновании.

Организация учебного процесса на этапе 2:

 

-С чего же мы начнём свой путь? (с повторения)

- А что мы будем повторять? (то, что пригодится на уроке для открытия новых знаний)

- Хорошо, приступим.

1. Сравнение  групп  предметов.

 - Выполните задание:

 

 

 

 

 

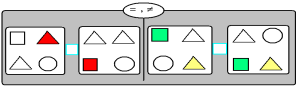
Фиксируется эталон  Э – 1 :

 

 

 

 

 

 

    2)  Способы задания множеств.

- Составьте и запишите  множество дней недели  А.

Дети работают на планшетах, один ребёнок у доски.

А= {понедельник; вторник; среда; четверг; пятница; суббота;  воскресенье}.

 

- Каким способом задано это множество? (общим свойством )

-Хорошо.

-Запишите множество  В. Его элементы: 1,3,5,7,9.

В= {1; 3; 5; 7; 9}.

 

- Каким способом задано множество В? (перечислением)

-А можно это же множество задать общим свойством? (да,  все элементы – однозначные нечётные числа – это их общее свойство)

- Молодцы! Какой эталон нам помог справиться с заданием? (эталон  « Способы задания множеств»)

На доске фиксируется   эталон   Э – 2 .

 

3)  Свойства множеств .

- Назовите, ребята, свойства, которыми обладает любое множество. (Все элементы собраны вместе, ни один из них не повторяется  и порядок записи элементов не важен )

На доске фиксируется эталон  Э – 3 .

 *  элементы собраны вместе

 *   элементы не повторяются

 *   порядок расположения элементов не важен

 

 4)   Тренинг мыслительных операций.

-Рассмотрите множество С.

 С = {11; 22; 33; 44;  55 …}

- Каким общим свойством обладают элементы множества С? (Двузначные числа, в записи которых используется одна цифра.)

-Почему после элемента 55 стоит многоточие? (Потому что  есть ещё числа, обладающие этим свойством.)

- Хорошо, тогда перечислите и впишите недостающие элементы множества.

С = {11; 22; 33; 44;  55; 66; 77; 88; 99}

 

-Почему остановились? (больше нет чисел, обладающих этим свойством, так потом идёт число 111 , а оно трехзначное, а значит нам не подходит )

- Хорошо, найдите сумму первого и последнего элементов, второго и предпоследнего, третьего и третьего с конца.

           Дети вычисляют, применяя эталон  Э-4.

 

 

 

Сумма 11 и 99 , 22 и 88 ,33 и 77 равна 110 .

 

-Что замечаете? (В ответе получается одно и то же число.)

- Дайте характеристику этому числу (Число 110 – трёхзначное, в разряде единиц 0, поэтому круглое, в записи числа в разрядах десятков и сотен одна цифра.)

 

- Молодцы! Давайте обобщим что же мы с вами повторили. (Сравнение групп

 предметов, различные способы задания множеств,  вспомнили свойства множеств,

 поработали с закономерностью, которой обладали элементы множества С – множества     двузначных чисел, в записи которых используется одна цифра.)

-Для чего мы  повторили именно эти правила, эталоны, способы действий? (они нам помогут  разобраться с  заданием на затруднение)

- Что же дальше? (наше пробное действие)

- Вы готовы? Хотите его услышать? (да)

- Тогда будьте внимательны!

Дано  множество А, заданное общим свойством элементов – множество осенних месяцев  и множество  В, заданное перечислением элементов  --

В = {сентябрь; октябрь; ноябрь; декабрь}

В течение 1 минуты запишите  эти множества и  обведите правильное (на ваш взгляд) утверждение:

        А  равно  В                              А  не равно  В

- Вам понятно задание? (Да.)

- Работайте на планшетах. Время пошло.

- Время закончилось. Предъявите ваши результаты.

Вероятно, все дети выполнят задание, хотя возможно кому-то не хватит времени. Рассмотрим разные варианты фиксации затруднения.

- У кого нет ответа? ( … )

-В чём ваше затруднение?  ( Я не смог справиться с заданием, мне не хватило времени)

- Кто выбрал ответ А равно В? У вас есть обоснование? (нет, мы не можем обосновать свой выбор)

- Кто выбрал вариант ответа А не равно В? Каким эталоном вы воспользовались? (у нас нет такого эталона)

Фиксируется затруднение

- Что же нам делать? (остановиться и подумать)

 

3. Выявление места и причины затруднения.

Цель:

           1) организовать восстановление выполненных операций и фиксацию

              ( вербальную и знаковую) места – шага, операции, где возникло затруднение;

         2) выявить и зафиксировать во внешней речи  причину (почему?)

               возникшего затруднения – отсутствие обоснования для заданий подобного типа.

Организация учебного процесса на этапе 3:

- Уточните, какое задание вы выполняли ? ( нужно было определить равны или не равны множество А, заданное  общим свойством – осенние месяцы  и множество

 В = {сентябрь; октябрь; ноябрь; декабрь} )

- Где возникло затруднение? ( В выборе  ответа, в обосновании ответа)

- Почему  возникло затруднение?  (мы не знаем, как сравнить два множества; у нас нет эталона, который помог бы обосновать наш выбор)

 

4. Построение проекта выхода из затруднения.

Цель: 

в коммуникативной форме организовать построение учащимися проекта будущих учебных действий:

           1) организовать фиксацию образовательной цели урока ( открыть способ действия,       позволяющий устанавливать  соотношение равно или не равно между  множествами )  и темы урока;

           2)  определить средства, необходимые для достижения цели;

           3) согласовать  план  проекта  выхода из затруднения.

Организация учебного процесса на этапе 4:

- Так какую цель мы  поставим  перед собой? (открыть способ действия или научиться определять, равны разные множества или нет)

- Какова же тема урока? (  Равны и не равные множества)

- Хорошо . В процессе урока мы подкорректируем тему , уточним её .

-Что нам пригодится в открытии новых знания? (эталон для сравнения групп предметов,

Свойства множеств …)

-С чего начнём работать? (нужно составить план)

Вывешивается карточка   Д – 6

  ПЛАН:

-Итак,  что нужно сделать сначала?

                     1.  Записать множества А  и  В.

-Хорошо, дальше?

                    2.  Каждому элементу множества А соотнести элемент множества В.

- Зачем? (посмотрим, что получится )

                    3.  Проанализировать.

 

4. Сделать вывод... (шаги   фиксируются на доске)

-Молодцы! План составили, теперь за работу.

 

5. Реализация построенного проекта.

Цель:

1. организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение новых знаний: умения  выявлять соотношения «равно» и «не равно» между множествами, информация о числе элементов множества, понятия « пустое множество »;
2. создать условия для  реализации плана, построенного детьми с целью добывания новых знаний;
3. организовать согласование способов и фиксацию построенного способа действия в речи и знаково (с помощью опорного конспекта);
4.  организовать уточнение общего характера.

Организация учебного процесса на этапе5:

Работа организуется в группах, с детьми необходимо актуализировать правила работы в группах (см. урок -1 , М-3 , ч-1 ;  правила имеются у каждого ребёнка )

В процессе работы в группах появляется примерно такая запись:

А – множество осенних месяцев, тогда  А = {сентябрь; октябрь; ноябрь}

В = {сентябрь; октябрь; ноябрь;  декабрь}

 

Так как в множестве А – 3 элемента, а в множестве В – 4 элемента и 3 элемента множества А соответствуют 3 элемента множества В  и  на 1 элемент в множестве В больше, чем в А, то множества А и В не равны.

Вывод:    А не равно В 

Представитель одной группы представляет работу, остальные дополняют.

-Хорошо , дети , МОЛОДЦЫ !

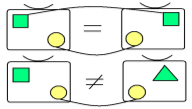
-А как записать это же математическим языком, подумайте.

На доске фиксируется запись:

                 А  =  В                                                А       В                     

 

- Давайте составим эталон. Запишите множество – его элементы  a , b , c  .

 –Хорошо.

                          А = {a , b , c}

-  Запишите множество  В с элементами b , a , c .

                          В = {b , a , c}

-Поставьте каждому элементу множества А элемент  множества В : 

 

 

Фиксируется на доске  Э – 5 .

Сформулируйте правило:

ЕСЛИ МНОЖЕСТВО СОСТОИТ ИЗ ОДНИХ И ТЕХ ЖЕ ЭЛЕМЕНТОВ, ТО МНОЖЕСТВА РАВНЫ.

-Хорошо, а как вы думаете порядок расположения  элементов в множестве  имеет значение или нет?

ПОРЯДОК РАСПОЛОЖЕНИЯ ЭЛЕМЕНТОВ НЕ ВАЖЕН (свойство множества )

- Ребята, как вы думаете, во множестве всегда несколько элементов? ( … )

- Сколько у любой кошки хвостов? (1)

-Значит, множество состоит из 1 элемента.

- Приведите примеры множеств, которые состоят тоже из 1 элемента.

 ( множество носов у человека, множество детей у Галины Владимировны, множество    глаз у циклопа)

- Так  какое число  элементов может быть во множестве? (1, 2 , разное и т. д.)

- Рассмотрим множество конфет в вазе на столе.

-Посмотрите, сколько конфет в вазе? (конфет нет, там  ваза пустая)

- Как вы думаете, как называют такое множество, в котором нет элементов? ( …)

 

- Правильно, пустое множество.

 - В математике существует такой символ:         он обозначает пустое множество.

 -Пустое множество записывается без скобок.

   На доске фиксируется запись Э – 6  .

Множество, не содержащее ни одного элемента, называется пустым.

                       {         } =

 

- А теперь, сформулируйте более точно тему урока (Равные и не равные множества).

Число элементов множества. Пустое множество.)

- Молодцы! Много новых знаний открыли. Как убедиться , что мы  правы? ( посмотреть в учебнике )

- Откройте учебник на странице 7 и прочитайте правило в рамочке.

 

6. Первичное закрепление во внешней речи.

Цель:

1. зафиксировать  во внешней речи понятия равного и не равного множества, пустого множества.

Организация учебного процесса на этапе 6:

•      Ребята, новые правила, эталоны вы добыли. Что нам нужно делать теперь? 

 ( потренироваться.)

       Задания  выполняются с комментированием  способов в громкой речи.

 

 

 

 

 

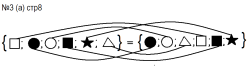
    Ставится соотнесение каждому элементу, так как каждому элементу множества 1 соответствует элемент множества 2 , то множества равны, обводим ответ да.

Составить D= A и D = B  ( № 5 , стр. 8 )

 

 

 

 

 

 

 

 

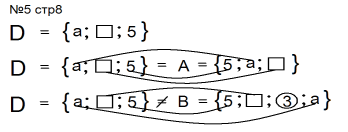
Возможны другие варианты множеств А и В, удовлетворяющие условию.

 

№ 3 (б, в, стр. 8 – в парах).

 На доске фиксируется подробный образец  Д – 9 .

- -Хорошо. Идём дальше./

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на новый способ действия: выявлять равные и не равные множества;

2)  организовать  самооценку детьми правильности выполнения задания (при необходимости организовать коррекцию выявленных ошибок).

Организация учебного процесса на этапе7:

- Ребята, вы открыли новое знание , потренировались . Что теперь нужно сделать ?

 ( самостоятельную работу)

- Хотите проверить себя? ( да )

- Самостоятельно выполняем № 4 , стр . 8 и № 6 (а), стр . 8 .

Учащиеся работают самостоятельно . время работы 2-3 минуты .

- Закончили работу (на доске фиксируется эталон для самопроверки  Д - 10)

- Проверьте себя по эталону для самопроверки, зафиксируйте  результат с помощью знаков « + » или «? ». 

 Дети выполняют самопроверку и фиксируют результат.

- Какие возникли затруднения? ( … )

- Исправьте ошибки.

- Поднимите руки у кого всё верно. ( … )

- Молодцы!

8. Включение в систему знаний и повторение.

Цель:

 1)  повторить  решение текстовых задач на разностное и кратное сравнение,                   составление буквенных выражений к текстовым задачам.

Организация учебного процесса на этапе 8:

1)Повторение задач  на разностное и кратное сравнение.

•      А какие задачи на сравнение чисел вы учились решать? («На» и «в» — разностное и кратное сравнение.)

Решим № 10 (а, б ). страница 9 .            ФРОНТАЛЬНАЯ РАБОТА,

На доске выставляются опорные схемы Д- 11.

9) таблицы для повторения задач на разностное и кратное сравнение (этап 8);

 

 

 

 

 

 

 

 

 

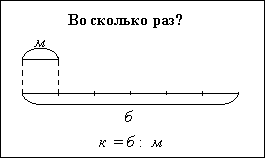
•      Как найти, на сколько одно число меньше или больше другого? Меньшее число? Большее число?
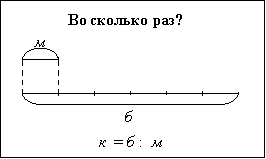
•      Как найти, во сколько раз одно число меньше или больше другого? Меньшее число? Большее число?

 

- Чтобы узнать, во сколько раз 56 >, чем 8 , нужно 56 : 8 =7 , 56> 8 в 7 раз.

- Чтобы узнать, во сколько раз 8 < 56 , нужно 56 : 8 = 7, 8 <56 в 7 раз.

 

2) Анализ и решение блиц – турнира  № 11, стр.9.

 

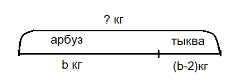
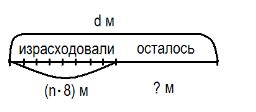
a)    a + a*9;      б) b + (b-2)         или       b + b-2;     в)   c – c : 7;     г)   d – n * 8

При составлении выражений следует обратить внимание детей на грамотное использование скобок.

  Так, например, в выражении   a + a*9 скобки не нужны, так как запись в скобках произведения  (а * 9) не изменит порядка действий. Напротив, во втором выражении отсутствие скобок изменяет ход решения задачи: запись   b + (b-2)         означает, что вначале ищется масса тыквы, а затем складывается с массой арбуза, а запись  b +  b-2

- что удвоенная масса арбуза уменьшается на 2 кг.

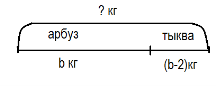
К задачам, которые могут вызвать затруднение, целесообразно заранее заготовить графические схемы и в случае необходимости разобрать решение по этим схемам, например  (Д-12):

 

 

 

 

 - Хорошо.

 

9. Рефлексия учебной деятельности на уроке.

Цель :

1.    зафиксировать в речи новый способ действий, изученный на уроке: понятия  «равные множества и не равные множества », « число  элементов

      множества », « пустое множество »;

2.    организовать рефлексивный анализ учебной деятельности на уроке с точки зрения требований, известных учащимся;
3.    зафиксировать неразрешённые  затруднения, которые остались,

      как направление будущей  учебной деятельности  и способы их преодоления ;

4.    оценить собственную деятельность на уроке;
5.    обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9 :

- Какую цель мы ставили на уроке? ( … )

- Какие множества являются равными? Зависит ли равенство от расположения

элементов?  ( … )

- Как вы понимаете термин « пустое множество »?

- Докажите, что вы находились в учебной деятельности на уроке. ( мы выполняли пробное задание, зафиксировали место и причину затруднения, …  )

•      Какие затруднения ещё остались, над, чем еще надо поработать? ( … )
•       
•      Оцените свою работу на уроке по  известным вам критериям  (см. урок -1, М – 3,

       ч – 1 .)

- А теперь домашнее задание:

 

 

Домашнее задание:

 Составить конспект с  новыми эталонами;

• № 6 (б), 8 (б);

☺ придумать и свой вариант равных и не равных множеств.