Рівномірний прямолінійний рух. Відносність руху.

Практичне заняття 2 (2години)

Тема: Рівномірний прямолінійний рух. Відносність руху.

Мета: навчальна: закріпити знання про рівномірний рух і відносності руху; виробляти вміння обчислювати прискорення, знаходити проекцію миттєвої швидкості за проекціями початкової швидкості і  прискоренням; формувати відповідні знання і  вміння щодо розв’язання основної задачі механіки.

розвивальна: розвивати мислення та увагу студентів.

виховна: виховувати творчі здібності; виховувати інтерес до фізики.

План практичного заняття

1. Ознайомлення студентів з поняттям рівномірного прямолінійного руху.
2. Ознайомлення студентів з поняттям відносності руху.
3. Розв’язування задач.

Література.

1. Генденштейн Л. Е.. Фізика.10 кл. : підруч. для загальноосвіт. навч. закладів : рівень стандарту/Л. Е. Генденштейн, І. Ю. Ненашев. - X. : Гімназія, 2010. - 272 с. : іл.
2. Коршак Є.В. Фізика: 10 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту / Є.В. Коршак, О.І. Ляшенко, В.Ф. Савченко. – К.: Генеза, 2010. – 192с.: іл.

Теоретичні відомості

Розглянемо найпростіший криволінійний рух тіла - рух по колу з незмінною за модулем швидкістю. Рівномірним рухом тіла по колу називають такий рух, при якому швидкість тіла змінюється за напрямом, але не змінюється за значенням.

Введемо основні величини, які характеризують рівномірний рух по колу.

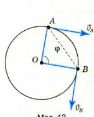Миттєва швидкість руху тіла при такому русі в кожній точці напрямлена по дотичній до траєкторії. Підтвердженням цього може бути відлітання шматочків речовини від точильного каменя, а також бризок від коліс велосипеда або автомобіля. Припустимо, що точка рівномірно рухається по колу радіуса Д і за певний час t переміщується з точки А в точку В.

Як видно з малюнка, лінійна швидкість руху тіла за модулем залишається

сталою (), але її напрям весь час змінюється. Тому в данному разі користуються поняттям миттєвої швидкості, яка визначає швидкість руху тіла в точці і напрямлена по дотичній до дуги в даній точці (точки А і В).

Отже, лінійна швидкість тіла, що рівномірно обертається по колу, весь час змінюється за напрямом і у будь-якій точці траєкторії напрямлена по дотичній до дуги цього кола, має стале значення.

Користуючись визначенням швидкості руху тіла для рівномірного прямолінійного руху, з’ясуємо, як визначається лінійна швидкість тіла у рівномірному русі по колу. Ми знаємо, що , де - пройдений тілом шлях. Тіло здійснює за певний час t один оберт, проходячи шлях, що дорівнює довжині кола l = 2nR. Тоді лінійна швидкість руху тіла під час рівномірного руху по колу визначається за формулою , де - лінійна швидкість руху тіла по колу; - радіус кола; - час руху тіла.

Кутова швидкість тіла - це фізична величина, яка показує, як швидко змінюється кут повороту тіла, і визначається відношенням зміни кута до інтервалу часу , за який ця зміна відбулася: .

Якщо за час t кут повороту тіла, яке обертається рівномірно, дорівнює , то кутову швидкість визначаємо із співвідношення: .

Одиницею кутової швидкості в СІ є радіан за секунду (1 рад/с). 1 рад/с дорівнює кутовій швидкості такого рівномірного руху по колу, під час якого за 1 секунду здійснюється кутове переміщення на 1 радіан. Період обертання - це час, протягом якого тіло робить один повний оберт по колу. Якщо тіло робить N обертів, то період обертання має вигляд. де t - час обертання; N - кількість зроблених обертів. Одиницею періоду обертання Т тіла є секунда (с). Величину, обернену до періоду обертання, називають частотою обертання: .Частота обертання тіла п визначає кількість обертів тіла навколо центра обертання за 1 секунду: .Одиницею частоти в СІ є оберт за секунду (об/с). 1об/с дорівнює такій частоті обертання, при якій тіло за 1с. робить 1оберт. Використовують й інші одиниці, наприклад оберт за хвилину: 1 об/хв = 1/60 об/с. Оскільки експериментально встановлено, що кутове переміщення за час, що дорівнює періоду Т, становить : рад, то кутова швидкість може бути визначена через період і частоту обертання: . Якщо пригадати, що лінійна швидкість тіла , то можна знайти її зв’язок з кутовою швидкістю: . Прискорення тіла, яке рівномірно рухається по колу, у будь-якій його точці  доцентрове, тобто напрямлене по радіусу кола до його центра. . Знаючи, що , формулу для розрахунку доцентрового прискорення можна записати у вигляді .

Практична частина

Приклади задач.

Електродвигун, зв’язаний ременевою передачею з токарним верстатом, обертається з частотою 980 об/хв. Діаметр шківа, надітого на вал двигуна, дорівнює 10см. Визначте діаметр шківа, надітого на вал верстата, якщо частота обертання вала 300 об/хв. Яка кутова швидкість обертання шківа верстата?

Яка швидкість руху автомобіля, якщо його колеса радіусом 30 см роблять 600 об/хв? Визначте доцентрове прискорення коліс автомобіля.

Розв’язати задачі.

1. Частота обертання вала генератора вітродвигуна дорівнює 30 об/хв, якоря електродвигуна 1500 об/хв, барабана сепаратора 8400 об/хв, шпинделя шліфувального верстата 96 000 об/хв. Обчисліть їх періоди обертання.
2. Частота обертання повітряного гвинта літака 1500 об/хв. Скільки обертів робить гвинт на шляху 90км при швидкості польоту 180 км/год?
3. Період обертання платформи карусельного верстата 4с. Визначте швидкість крайніх точок платформи, що віддалені від осі обертання на 2 м.

Питання для опитування

1. Чому стіл у класі одночасно перебуває у спокої й русі?
2. Чому шлях, пройдений тілом під час руху, є скалярною величиною?
3. Чому не можна робити обчислення за формулами, записаними у векторній формі?
4. Чому формула для розрахунку швидкості рівнозмінного руху тіла має два знаки: ?

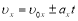4. Чому графіком швидкості рівноприскореного руху є пряма лінія?

5. Чому графік швидкості рівносповільненого руху тіла ніколи не проходить через початок координат?
6. Чому вільне падіння - це рівноприскорений рух?
7. Чому швидкість руху тіла 5 м/с у прямолінійному рівномірному русі - це не те саме, що 5 м/с - швидкість рівномірного руху тіла по колу?
8. Чому учень припустився грубої помилки, коли відповів так: «Переміщення матеріальної точки - це відрізок прямої, ш;о з’ єднує початкову точку руху з кінцевою»?