Різні аспекти використання методу математичної індукції у школі
Ю. В. Власюк
РІЗНІ АСПЕКТИ ВИКОРИСТАННЯ МЕТОДУ МАТЕМАТИЧНОЇ ІНДУКЦІЇ У ШКОЛІ

Луцький район
Берестечківська територіальна громада
ЗЗСО Берестечківський ліцей
Ю. В. Власюк
РІЗНІ АСПЕКТИ ВИКОРИСТАННЯ МЕТОДУ МАТЕМАТИЧНОЇ ІНДУКЦІЇ У ШКОЛІ
Методична розробка
Власюк Ю. В. - учитель математики ЗЗСО
Берестечківський ліцей
Різні аспекти використання методу
Математичної індукції у школі
Методична розробка. – 90 с.
Дана розробка присвячена застосуванню методу математичної індукції, його основних формул та властивостей. Матеріал буде корисним при читанні шкільного курсу математики, а також на факультативних заняттях в школі.
Зміст
Вступ…………………………………………………………..6
Розділ 1. Дедукція та індукція 10
Розділ 2. Метод математичної індукції ..18
2.1 Вправи для самостійної роботи………………….........…24
Розділ 3. Застосування методу математичної індукції при розв’язуванні різних типів шкільних задач. .25
3.1. Застосування методу математичної індукції при розв’язуванні задач на подільність чисел ....25
3.1.1 Вправи для самостійної роботи…………………......…39
3.2. Застосування методу математичної індукції при розв’язуванні задач на знаходження сум та добутків…..….39
3.2.1 Вправи для самостійної роботи…………………......…49
3.3. Доведення тотожностей і нерівностей методом математичної індукції………………………………..……….49
3.3.1 Вправи для самостійної роботи…………………......….68
3.4. Застосування методу математичної індукції при розв’язуванні геометричних задач ….68
3.4.1 Вправи для самостійної роботи…………………......…73
3.5. Застосування методу математичної індукції при розв’язуванні задач, пов’язаних з рекурентним способом задання послідовностей. 73
3.5.1 Вправи для самостійної роботи…………………......…75
3.6. Застосування методу математичної індукції при виведенні формули n-го члена і суми перших n членів арифметичної і геометричної прогресій …76
3.6.1 Вправи для самостійної роботи…………………......…81
3.7. Застосування методу математичної індукції в тригонометрії 81
3.7.1 Вправи для самостійної роботи…………………......…89
Список використаної літератури 90
ВСТУП
Метод математичної індукції застосовується в найрізноманітніших областях математики і не тільки. Оскільки цей метод по суті пов’язаний з поняттям числа, то найчастіше він застосовується в арифметиці, алгебрі і теорії чисел. Проте поняття цілого числа є основним не тільки в цих розділах математики, а й, наприклад, в геометрії, тригонометрії. Зокрема, застосування цього методу в геометрії особливо цікаві і ефективні.
За індукцією не тільки зручно проводити доведення, а і давати деякі означення.
Досить часто в математиці використовують дедуктивний спосіб побудови теорії. Дедуктивне міркування - це міркування від загального до конкретного, тобто міркування, вихідним моментом якого є загальне твердження, а заключним моментом - частинний висновок, а індуктивні висновки - це зроблені на основі спостережень і дослідів, тобто отримані шляхом розгляду окремих випадків і подальшого розповсюдження помічених закономірностей на загальний випадок. Роль індуктивних висновків в експериментальних науках дуже велика. Вони дають змогу довести ті положення, з яких потім шляхом дедукції робляться подальші висновки. У математиці індукція часто дозволяє передбачити яким повинно бути формулювання теореми, а в ряді випадків і намітити шляхи її доведення. Саме цим визначається актуальність нашого дослідження.
Метод математичної індукції можна порівняти з прогресом. Ми починаємо з нижчого, в результаті логічного мислення приходимо до вищого. Хоча і виросла область застосування методу математичної індукції, в шкільній програмі йому відводиться мало часу. А це так важливо - вміти міркувати індуктивно. Говорячи про важливість цього методу, А.Н.Колмогоров зазначав, що «розуміння та вміння застосовувати принцип математичної індукції є хорошим критерієм зрілості, яка абсолютно необхідна математику».
Мета даного посібника - надати методичні рекомендації щодо вивчення даної теми на уроках алгебри в класах з поглибленим вивченням математики (8-9 класи), профільних класах (10-11 класи), систематизувати матеріал для проведення факультативних занять, підготовки учнів до олімпіад, підготовки до захисту науково - дослідницьких робіт в системі МАН України.
У математиці всі твердження можна умовно розділити на загальні та часткові. Загальні твердження виражають властивості групи об’єктів (чисел, геометричних фігур тощо). Часткові твердження виражають властивості конкретного об’єкта.
Наприклад, до загальних можна віднести такі твердження:
1) у будь-якому трикутнику сума довжин двох його сторін більша довжини третьої сторони;
2) усі цілі числа, які закінчуються парною цифрою, діляться на 2;
3) сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів дорівнює вільному члену:
![]()
х1, х2 – корені рівняння,
х1+ х2 = -р; х1 ⋅ х2 = q;
4) сума мір протилежних кутів вписаного в коло чотирикутника
дорівнює 1800.
До часткових можна віднести такі твердження:
 ● у трикутнику АВС (рис.1.1) сума довжин сторін АВ та ВС більша довжини третьої сторони АС;
● у трикутнику АВС (рис.1.1) сума довжин сторін АВ та ВС більша довжини третьої сторони АС;
● число 136 ділиться на 2;
 ● у зведеному квадратному рівнянні
● у зведеному квадратному рівнянні ![]() сума коренів дорівнює 5, а добуток коренів
сума коренів дорівнює 5, а добуток коренів
дорівнює 6;
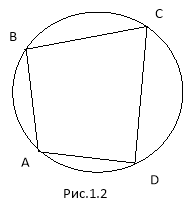
● у чотирикутнику ABCD, вписаному в коло,
∠А + ∠С = 1800, ∠B + ∠D = 1800 (рис.1.2)
Метод мислення, який полягає в переході від загальних тверджень до часткових, називається дедукцією (саме слово “дедукція” означає висновок). Однією з особливостей математики є дедуктивна побудова теорії, при якій усі твердження виводяться з кількох основних положень, які називаються аксіомами, та раніше доведених тверджень (теорем). Кожна теорема є загальним твердженням. Теореми ми доводимо саме для того, щоб потім використовувати їх для розв’язування різних конкретних задач, які є частковими випадками застосування загальних тверджень.
Дедукція – це не єдиний метод наукового мислення.
Індукція – метод мислення, який полягає у виведенні загальних висновків з розгляду окремих випадків. Це дослідницький метод, який веде до узагальнень на підставі експериментів і спостережень фактів, а також формулювання та перевірки гіпотез.
Наприклад, ми завжди можемо спостерігати, що течія річки Дніпро має певний напрям. Можна бути практично впевненим в тому, що і надалі Дніпро буде текти в тому ж напрямку, а не в протилежному. Інший приклад: завжди сонце сходило на сході, а заходило на заході. Це ж саме можна спостерігати і далі. Ці індуктивні висновки правильно описують ті спостереження, які ми проведемо будь-якого наступного дня. Роль індуктивних висновків в експериментальних науках дуже велика. Вони дають можливість сформулювати закони, за допомогою яких можна пояснити різні явища. Теоретична механіка базується на трьох законах Ньютона, а самі ці закони були результатом великої кількості узагальнених дослідних даних.
Індуктивні міркування широко застосовував у своїх дослідженнях з теорії чисел член Петербурзької Академії наук, великий математик XVIII століття Леонард Ейлер. Історія зберегла такий вислів Ейлера:
“У мене немає для доведення ніяких інших переконань, за винятком довгої індукції, яку я провів так далеко, що ні в якому разі не можу сумніватися в законі, що керує утворенням цих членів… І здається неможливим, щоб закон, який, як було виявлено, виконується, наприклад, для 20 членів, не можна було б спостерігати і для наступних”.
На відміну від дедукції індукція може привести як до правильних, так і до неправильних висновків. Наведемо приклади, які спростовують висновок Ейлера.
Приклад 1. Розглядаючи значення квадратного тричлена
f(n) = n2 + n + 41 при малих натуральних значеннях n, можна помітити, що ці значення будуть простими числами.
Дійсно: f(1) = 43;
f(2) = 47;
f(3) = 53;
f(4) = 61.
Таким чином, нібито можна зробити висновок, що при будь-якому натуральному n значення виразу n2 + n + 41 є простим числом. Однак, цей висновок неправильний. Якщо n = 41, то
f(41) = 412 + 41 + 41 = 41· (41 + 1 + 1) = 41· 43.
Цей результат є числом складеним.
Приклад 2. Французький математик XVII століття П’єр Ферма, розглядаючи числа
![]() + 1 = 5,
+ 1 = 5, ![]() + 1 = 17,
+ 1 = 17, ![]() + 1 = 257,
+ 1 = 257, ![]() + 1 = 65537,
+ 1 = 65537,
зробив висновок, користуючись індуктивним методом, що при будь-якому натуральному значенні n число ![]() + 1 є простим.
+ 1 є простим.
Однак, Ейлеру вдалося показати, що число ![]() + 1 ділиться на 641.
+ 1 ділиться на 641.
Існують приклади, коли число, яке заперечує гіпотезу, настільки велике, що знайти його дуже складно.
Приклад 3.
Нехай сформульована гіпотеза: «При будь-якому натуральному значенні n число 991n2 + 1 не буде точним квадратом деякого натурального числа».
Для заперечення цього твердження довелося перебрати велику кількість чисел, адже перше значення n таке, що 991n2 + 1 є точним квадратом деякого натурального числа, має 29 цифр.
Якщо загальний висновок робиться на основі розгляду лише окремих можливих випадків, то такий метод міркувань називається неповною індукцією.
Отже, сформульоване за допомогою індукції загальне твердження підлягає доведенню. У деяких випадках таке доведення можна провести, розглянувши скінченну кількість усіх можливих випадків.
Наприклад, щоб довести, що для будь-якого правильного багатогранника справедливе співвідношення В – Р + Г = 2, де В – кількість його вершин, Р – ребер, Г – граней, достатньо розглянути п’ять випадків: тетраедр, октаедр, гексаедр (куб), додекаедр, ікосаедр – інших правильних багатогранників не існує (рис.2).

1 – тетраедр, 2 – гексаедр (куб), 3 – октаедр, 4 – додекаедр, 5 - ікосаедр
Рис.2. Правильні багатогранники
А для цих п’яти випадків твердження можна перевірити за допомогою наступної таблиці:
|
№ з/п |
Багатогранник |
Кількість вершин |
Кількість ребер |
Кількість граней |
|
1 |
Тетраедр |
4 |
6 |
4 |
|
2 |
Октаедр |
6 |
12 |
8 |
|
3 |
Гексаедр (куб) |
8 |
12 |
6 |
|
4 |
Додекаедр |
20 |
30 |
12 |
|
5 |
Ікосаедр |
12 |
30 |
20 |
Метод доведення загального твердження, який полягає в розгляді скінченної кількості всіх можливих випадків, називається повною індукцією.
З методом повної індукції ви вже зустрічалися раніше, розглядаючи, наприклад, доведення теореми про міру вписаного в коло кута. Доведення теореми зводиться до розгляду трьох випадків (рис.3).
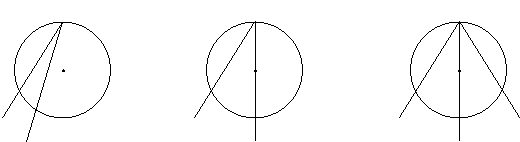
Рис.3. Три випадки розміщення вписаного кута в колі
Метод повної індукції має досить обмежену область застосування в математиці, бо, як правило, математичні твердження стосуються нескінченної множини об’єктів (наприклад, всіх натуральних чисел, всіх простих чисел, всіх багатогранників і т.д.) і перебрати всі ці об’єкти неможливо.
Розділ 2.
Нехай деяке твердження справедливе в кількох окремих випадках. Розгляд усіх інших випадків або взагалі неможливий, або потребує розгляду великої кількості випадків. Як же дізнатися, чи буде правильним твердження в усіх можливих випадках? Це питання часто вдається розв’язати, використовуючи метод математичної індукції.
Основна заслуга в розробці цього методу належить французьким математикам Блезу Паскалю (1623-1662) і Рене Декарту (1596-1650), а також швейцарському математику Якобу Бернуллі (1654-1705).
В основі методу математичної індукції лежить твердження, яке називається принципом математичної індукції:
Деяке твердження правильне при будь-якому натуральному n, якщо:
1) воно правильне при n = 1;
2) із правильності цього твердження при будь-якому k слідує, що воно правильне і при k + 1.
Позначимо Т(n) твердження, яке залежить від натурального числа n.
Доведення методом математичної індукції проводиться за таким алгоритмом:
1) перевірити правильність твердження Т(1);
2) припустити, що правильним є твердження Т(k), k ![]() 1;
1;
3) довести, використовуючи це припущення, що правильним буде твердження Т(k+1);
4) зробити висновок, що за принципом математичної індукції твердження Т(n) правильне для будь-якого n![]() N.
N.
Перший крок алгоритму називається базисом (початком) індукції, другий крок – припущенням індукції, а третій – індуктивним кроком.
З’ясуємо основу цього методу.
Поняття натурального числа часто вважається само собою очевидним, таким, що не потребує пояснення. Проте в сучасній математиці не допускається використання таких само собою очевидних понять. Кожне поняття повинно бути означене на основі раніше означених понять. Для арифметики основними (неозначуваними) поняттями є: одиниця, натуральне число і " слідувати за", а основними властивостями цих понять – аксіоми, сформульовані італійським математиком Джузеппе Пеано (1858-1932). Ці аксіоми такі:
1) для кожного натурального числа n існує одне і тільки одне натуральне число, що слідує за ним. Це число прийнято позначати n′ (або n+1);
2) одиниця є натуральним числом, причому вона не слідує ні за яким натуральним числом;
3) жодне натуральне число не слідує за двома різними натуральними числами;
4) якщо множина А містить одиницю і разом з кожним числом k містить наступне за ним число k′ (чи k+1), то А містить всі натуральні числа.
Четверту аксіому Пеано називають аксіомою математичної індукції – саме на ній оснований метод математичної індукції.
Нехай твердження Т(1) – правильне, а з правильності твердження T(k) слідує правильність твердження T(k+1). Нехай А - множина тих натуральних чисел, для яких правильне T(n). За припущенням 1∈А (твердження правильне при n=1), а з того, що k ∈ A слідує k+1 ∈ A (якщо T(n) правильне при n=k, то воно правильне і при n=k+1). Тоді в силу аксіоми (4) звідси слідує, що А співпадає з множиною всіх натуральних чисел. Значить, T(n) правильне для всіх натуральних чисел.
Метод математичної індукції застосовується при розв’язуванні задач на подільність; задач на знаходження сум; при доведенні тотожностей і нерівностей. За допомогою цього методу можна вивести формули n-го члена і суми перших n членів арифметичної і геометричної прогресій. Серед вправ зустрічаються також задачі, пов’язані з рекурентним способом задання послідовності; за допомогою даного методу розв’язуються деякі геометричні задачі, а також доводяться тригонометричні тотожності і нерівності.
Розглянемо розв’язки наступних задач.
Приклад 1.
Довести що для будь – якого натурального n ![]() N
N
|
n(2n2 - 3n + 1) ділиться на 6, |
P(1) – істинне твердження (0 ділиться на 6). Нехай P(n) справедливе, тобто n(2n2 - 3n + 1) = n(n - 1)(2n - 1) ділиться на 6. Покажемо, що тоді істинне P(n + 1), тобто, (n + 1)n(2n + 1) ділиться на 6. Дійсно, оскільки
|
n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) = |
|
= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n = |
|
= n(n - 1)(2n - 1) + 6n2 |
і, так як n(n - 1)(2n - 1), так і 6n2 ділиться на 6, тоді і їх сума n(n + 1)(2n + 1) ділиться 6.
Таким чином, P(n + 1) – справедливе твердження, звідси випливає, що n(2n2 - 3n + 1) ділиться на 6 для будь-якого n ![]() N.
N.
Приклад 2.
Знайти формулу для обчислення суми
Sn=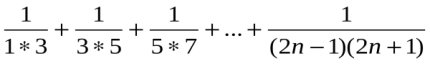 .
.
Використаємо неповну індукцію. Розглянемо частинні випадки:
n=1 S1=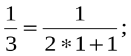
n=2 S2=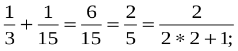
n=3 S3=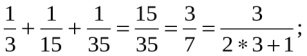
n=4 S4=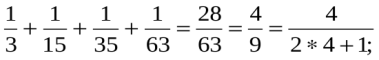
Можна зробити припущення, тобто виказати гіпотезу, що Sn=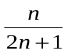 .
.
Доведемо цю формулу методом математичної індукції.
Доведення
1) Базис індукції: При n=1 S1=![]() =
=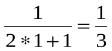 формула вірна.
формула вірна.
2) Індуктивний перехід:
Припустимо, що дана рівність має місце при n=k, тобто 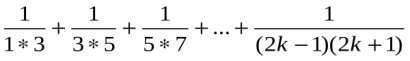 =
=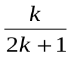 .
.
Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто, що
Sk+1=![]()
Враховуючи припущення маємо: Sk+1=![]() =
=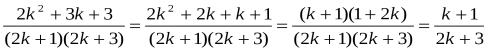 .
.
Отже формула вірна і при n=k+1. За принципом математичної індукції вона справджується і при будь-якому n.
2.1 Вправи для
самостійної роботи
Застосування методу математичної індукції при розв’язуванні різних типів шкільних задач.
3.1. Застосування методу математичної індукції при розв’язуванні задач на подільність чисел
Приклад 1.1.
Довести, що значення виразу n3 + 5n ділиться на 6, ∀n![]() N.
N.
Доведення.
При n = 1 значення виразу 13 + 5⋅1 ділиться на 6.
Припустимо, що на 6 ділиться значення виразу k3 + 5k.
Доведемо, що значення виразу (k+1)3 + 5(k+1) також буде ділитися на 6.
(k+1)3 + 5(k+1) = k3 + 3k2 + 3k + 1 + 5k + 5 = k3 + 5k + 3k2 + 3k + 6 = k3 + 5k + 3k (k + 1) + 6.
(k3 + 5k)![]() 6 (за припущенням), 3k (k + 1) ділиться на 3, а також на 2, оскільки добуток k (k + 1) двох послідовних натуральних чисел – парний, тобто 3k (k + 1)
6 (за припущенням), 3k (k + 1) ділиться на 3, а також на 2, оскільки добуток k (k + 1) двох послідовних натуральних чисел – парний, тобто 3k (k + 1) ![]() 6.
6.
Отже, значення виразу (k+1)3 + 5(k+1) ділиться на 6.
Згідно принципу математичної індукції (n3 + 5n) ![]() 6
6 ![]() n
n![]() N.
N.
Приклад 1.2.
Довести, що значення виразу ![]() ділиться на 19 при будь-якому натуральному n.
ділиться на 19 при будь-якому натуральному n.
Доведення.
Якщо n = 1, то ![]() .
.
Припустимо, що для деякого натурального k (k ≥ 1) значення виразу ![]() ділиться на 19.
ділиться на 19.
Доведемо, що значення виразу ![]() також ділиться на 19.
також ділиться на 19.
Дійсно,

Зважаючи на те, що ![]() і
і ![]() , то і вся сума буде
, то і вся сума буде
ділитися на 19, а отже, ![]() ділиться на 19, тому значення виразу
ділиться на 19, тому значення виразу
![]() ділиться на 19 при будь-якому натуральному n.
ділиться на 19 при будь-якому натуральному n.
Приклад 1.3.
Доведіть, що при будь-якому натуральному n значення виразу 7n⋅23n - 32n кратне 47.
Доведення.
Якщо n = 1, то 7⋅23 - 32 = 47 ![]() 47.
47.
Припустимо, що для деякого натурального значення k (k ≥ 1) значення виразу 7k⋅23k - 32k ділиться на 47.
Доведемо, що значення виразу 7k+1⋅23(k+1) - 32(k+1) ділиться на 47.
7k+1⋅23(k+1) - 32(k+1) = 7⋅7k⋅23k⋅23 – 32k⋅32 = 56⋅7k⋅23k - 9⋅32k =
= ![]()
Оскільки кожний доданок останньої суми ділиться на 47, то і сама сума, а отже, і значення виразу 7k+1⋅23(k+1) - 32(k+1) ділиться на 47.
Згідно принципу математичної індукції значення виразу 7n⋅23n - 32n ділиться на 47 при будь-якому натуральному значенні n.
Приклад 1.4.
Доведіть, що при будь-якому натуральному n значення виразу 22n-1 – 9n2 + 21n – 14 ділиться на 27.
Доведення.
Якщо n = 1, то 22⋅1-1 – 9⋅12 + 21⋅1 – 14 = 0 ![]() 27.
27.
Припустимо, що (22k-1 – 9k2 + 21k – 14) ![]() 27.
27.
Доведемо, що на 27 буде ділитися значення виразу
22(k+1)-1 – 9(k+1)2 + 21(k+1) – 14.
22(k+1)-1 – 9(k+1)2 + 21(k+1) – 14 = 22k+1 – 9k2 – 18k – 9 + 21k + 21 – 14=
=22k-1+2 – 9k2 + 3k – 2 = 4⋅22k-1 – 9k2 + 3k – 2 =
= 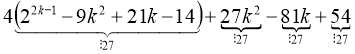 .
.
Таким чином, значення виразу 22(k+1)-1 – 9(k+1)2 + 21(k+1) – 14 ділиться на 27.
Згідно принципу математичної індукції значення виразу
22n-1 – 9n2 + 21n – 14 ділиться на 27 при ![]() n
n ![]() N.
N.
Теорема 1.1. Якщо n – натуральне число, то n2 – n – парне число.
Доведення.
Доведемо цю теорему методом математичної індукції.
1) Якщо n=1, то 12 – 1 = 0 – парне число.
2) Припустимо, що k2 – k – парне число. Доведемо, що
(k+1)2 – (k+1) також парне число.
(k+1)2 – (k+1) = k2 + 2k + 1 – k – 1 = k2 – k + 2k. Сума двох парних чисел є число парне.
Таким чином, парність n2 – n доведена при n=1, а із парності k2 – k доведена парність (k+1)2 – (k+1), тому згідно принципу математичної індукції робимо висновок, що n2 – n набуває парних значень при всіх натуральних значеннях n.
Теорема доведена.
Теорема 1.2. (мала теорема Ферма).
Значення виразу np – n, де p – просте число, ділиться на р.
Доведення.
Для доведення теореми нагадаємо формулу бінома Ньютона:
![]() .
.
 .
.
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
2 |
1 |
|
|
|
|
||||||||||||||||||
|
|
|
1 |
3 |
3 |
1 |
|
|
|
- трикутник Паскаля |
|||||||||||||||||
|
|
1 |
4 |
6 |
4 |
1 |
|
|
|
||||||||||||||||||
|
1 |
5 |
10 |
10 |
5 |
1 |
|
|
|||||||||||||||||||
|
. |
. |
. |
. |
. |
. |
. |
. |
|
||||||||||||||||||
![]() ,
, ![]() ,
, ![]() - третій рядок трикутника Паскаля.
- третій рядок трикутника Паскаля.
![]() ,
, ![]() ,
, ![]() ,
, ![]() - четвертий рядок трикутника Паскаля.
- четвертий рядок трикутника Паскаля.
………………………………….
![]() - n +1-ший рядок трикутника Паскаля.
- n +1-ший рядок трикутника Паскаля.
Доведення малої теореми Ферма будемо проводити методом математичної індукції.
1. Якщо n=1, то ![]() – 1 = 0
– 1 = 0 ![]() р.
р.
2. Нехай і ![]() , k ≥ 1. Доведемо, що на р буде ділитися значення виразу (k + 1)p – (k + 1).
, k ≥ 1. Доведемо, що на р буде ділитися значення виразу (k + 1)p – (k + 1).
Розглянемо різницю
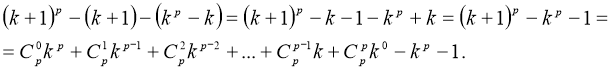
Враховуючи те, що 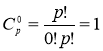 і
і 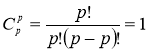 , то
, то
![]() (1)
(1)
Якщо 1 ≤ j < p, то всі числові коефіцієнти будуть такими:

Оскільки число р – просте, то воно не ділиться на жодне з чисел
1, 2, 3, …j-1, j, які є в знаменнику, тому ![]() ділиться на р, при 1 ≤ j < p. Але тоді всі доданки в правій частині рівності (1) діляться на р. Враховуючи те, що за припущенням
ділиться на р, при 1 ≤ j < p. Але тоді всі доданки в правій частині рівності (1) діляться на р. Враховуючи те, що за припущенням ![]() ділиться на р, то й
ділиться на р, то й ![]() також буде ділитися на р.
також буде ділитися на р.
Отже, ![]() ділиться на просте число р при будь-якому натуральному значенні n.
ділиться на просте число р при будь-якому натуральному значенні n.
Теорема доведена.
Кожний крок алгоритму, який застосовується при доведенні методом математичної індукції, важливий. Не слід думати, що, наприклад, перший крок алгоритму менш важливий, ніж решта кроків. Розглянемо приклад, з якого слідує те, до якого неправильного висновку можна прийти, якщо не переконатися в тому, що виконується перший крок алгоритму.
Приклад 1.5.
При будь-якому натуральному n число 2n + 1 – парне.
Доведення.
Нехай це твердження правильне при n = k, тобто число 2k + 1 – парне. Доведемо, що число 2(k + 1) + 1 – також парне.
Дійсно, 2(k + 1) + 1 = (2k + 1) + 2.
За припущенням число 2k + 1 парне, а тому сума його з числом 2 також буде парним числом.
Отже, твердження правильне при будь-якому натуральному n.
Ми б не прийшли до такого неправильного висновку, якби переконалися в тому, що число 2n + 1– непарне при n = 1.
Приклад 1.6
Довести, що (11n+2+122n+1) ділиться на 133 без залишку.
Доведення:
1) Нехай n = 1, тоді
113+123=(11+12)(112-132+122)=23´133.
(23´133) ділиться на 133 без залишку, значить при n = 1 твердження вірне.
2) Припустимо, що (11k+2+122k+1) ділиться на 133 без залишку.
3) Доведемо, що в такому випадку (11k+3+122k+3) ділиться на 133 без залишку. Насправді
11k+3+122k+3=11´11k+2+122´122k+1=11´11k+2+
+(11+133)´122k+1=11(11k+2+122k+1)+133´122k+1.
Отримана сума ділиться на 133 без залишку, тому що перше її доданок ділиться на 133 без залишку за припущенням, а в другому одним з множників виступає 133.
Отже, А(k)ÞА(k+1). В силу методу математичної індукції твердження доведено.
Приклад 1.7
Довести, що при будь-якому n 7n-1 ділиться на 6 без залишку.
Доведення:
1) Нехай n = 1, тоді Х1=71-1=6 ділиться на 6 без залишку. Значить при n = 1 твердження вірне.
2) Припустимо, що при n = k 7k-1 ділиться на 6 без залишку.
3) Доведемо, що твердження справедливе для n = k 1.
Xk+1=7k+1-1=7´7k-7+6=7(7k-1)+6.
Перший доданок ділиться на 6, оскільки 7k-1 ділиться на 6 по припущенню, а другим доданком є 6. Значить 7n-1 кратно 6 при будь-якому натуральному n.
В силу методу математичної індукції твердження доведено.
Приклад 1.8
Довести, що 33n-1+24n-3 при довільному натуральному n ділиться на 11.
Доведення:
1) Нехай n = 1, тоді
Х1=33-1+24-3=32+21=11
ділиться на 11 без залишку. Значить, при n = 1 твердження вірне.
2) Припустимо, що при n = k
Xk=33k-1+24k-3
ділиться на 11 без залишку.
3) Доведемо, що твердження вірне для n = k 1.
Xk+1=33(k+1)-1+24(k+1)-3=33k+2+24k+1=33´33k-1+24´24k-3=
=27´33k-1+16´24k-3=(16+11)´33k-1+16´24k-3=16´33k-1+
+11´33k-1+16´24k-3=16(33k-1+24k-3)+11´33k-1.
Перший доданок ділиться на 11 без залишку, оскільки 33k-1+24k-3 ділиться на 11 по припущенню, друге ділиться на 11, тому що одним з його множників є число 11. Значить і сума ділиться на 11 без залишку при будь-якому натуральному n.
В силу методу математичної індукції твердження доведено.
Приклад 1.9
Довести, що 112n-1 при довільному натуральному n ділиться на 6 без залишку.
Доведення:
1) Нехай n = 1, тоді 112-1=120 ділиться на 6 без залишку. Значить при n = 1 твердження вірне.
2) Припустимо, що при n = k 112k-1 ділиться на 6 без залишку.
3) Доведемо, що твердження вірне при n = k +1
112(k+1)-1=121´112k-1=120´112k+(112k-1).
Обидва з доданків діляться на 6 без залишку: перше містить кратне 6-ти число 120, а друге ділиться на 6 без залишку по припущенню. Значить і сума ділиться на 6 без залишку.
В силу методу математичної індукції твердження доведено.
Приклад 1.10
Довести, що 33n+3-26n-27 при довільному натуральному n ділиться на 262(676) без залишку.
Доведення:
Попередньо доведемо, що 33n+3-1 ділиться на 26 без залишку.
1) При n = 0
33-1 = 26 ділиться на 26
2) Припустимо, що при n = k
33k+3-1 ділиться на 26
3) Доведемо, що затвердження вірно при n = k+1.
33k+6-1=27´33k+3-1=26´33л+3+(33k+3-1) -ділиться на 26
Тепер проведемо доказ твердження, сформульованого в умові завдання.
1) Очевидно, що при n = 1 твердження вірне 33+3-26-27=676
2) Припустимо, що при n = k вираз 33k+3-26k-27 ділиться на 262 без залишку. 3) Доведемо, що твердження вірне при n = k+1
33k+6-26(k+1)-27=26(33k+3-1)+(33k+3-26k-27).
Обидва з доданків діляться на 262, перше ділиться на 262, тому що ми довели подільність на 26 виразу, що стоїть в дужках, а друге ділиться за припущенням індукції.
В силу методу математичної індукції твердження доведено.
3.1.1 Вправи для самостійної роботи
3.2. Застосування методу математичної індукції
при розв’язуванні задач на знаходження сум та добутків
Приклад 2.1.
Знайти суму перших n чисел натурального ряду.
Розв’язання.
Спочатку знайдемо суми двох, трьох, чотирьох, п’яти перших натуральних чисел, щоб виявити певну закономірність:
1 + 2 = 3, коли n = 2 ![]() ;
;
1 + 2 + 3 = 6, коли n = 3 ![]() ;
;
1 + 2 + 3 + 4 = 10, коли n = 4 ![]() ;
;
1 + 2 + 3 + 4 + 5 = 15, коли n = 5 ![]() .
.
Таким чином можна припустити, що
1 + 2 + 3 + ... + n = ![]() .
.
Доведемо цю рівність методом математичної індукції.
Якщо n = 1, то ![]() - правильне твердження.
- правильне твердження.
Припустимо, що правильною є рівність:
![]() .
.
Доведемо, що ![]() .
.
1 + 2 + 3 + ...+(k+1) = 1 + 2 + 3 + k + (k +1) =
![]()
Отже, згідно принципу математичної індукції рівність
1 + 2 + 3 + ... + n = ![]() правильна при
правильна при ![]() n
n ![]() N.
N.
Приклад 2.2.
Знайти суму перших n непарних чисел.
Розв’язання.
Розглянемо послідовні суми непарних чисел:
1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, …
Отримаємо числа 1, 4, 9, 16, … , які є квадратами натуральних чисел 1, 2, 3, 4.
Отже, можна припустити, що для будь-якого натурального числа n правильною буде рівність:
1 + 3 + 5 + … + (2n – 1) = n2.
Доведемо цю рівність методом математичної індукції.
Якщо n = 1, то 1 = 12 – твердження правильне.
Припустимо, що твердження правильне при будь-якому натуральному k, тобто 1 + 3 + 5 + … + (2(k –1) –1) + (2k – 1) = k2.
Доведемо правильність твердження для k + 1.
1 + 3 + 5 + … + (2(k –1) –1) + (2k –1) + (2(k +1) -1) = k2 + (2(k +1) –1) = k2 + 2k + 1 = (k +1)2.
Отже, згідно принципу математичної індукції
1 + 3 + 5 + … + (2n – 1) = n2 – правильна рівність при ![]() n
n![]() N.
N.
Приклад 2.3.
Знайти суму 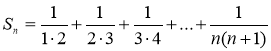 .
.
Розв’язання.
Спочатку знайдемо суми одного, двох, трьох і чотирьох доданків:
![]()
![]()
![]()
![]()
Можна припустити, що ![]()
Для доведення цієї гіпотези використаємо метод математичної індукції:
1) Якщо n = 1, то ![]() - твердження правильне.
- твердження правильне.
2) Припустимо, що твердження правильне при n = k (k ≥1), тобто
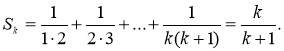
Використовуючи припущення, доведемо, що твердження буде правильним і при n = k + 1, тобто:


Отже, рівність ![]() правильна при будь-якому натуральному n.
правильна при будь-якому натуральному n.
Деякі твердження справедливі не для всіх натуральних n, а лише для натуральних n, починаючи з деякого числа m. Такі твердження іноді вдається довести методом, який дещо відрізняється від самого методу математичної індукції, але дуже схожим з ним. Він базується на такому принципі:
Твердження правильне при всіх натуральних значеннях n ≥ m, якщо:
1) воно правильне при n = m;
2) із правильності цього твердження при n = k, де k ≥ m, слідує, що воно правильне і при n = k +1.
В даному випадку був використаний узагальнений принцип методу математичної індукції.
Це твердження називається узагальненим принципом математичної індукції.
Доведення узагальненим методом математичної індукції проводиться за таким алгоритмом:
1) перевірити правильність твердження Т(m);
2) припустити, що правильним є твердження T(k), де k ≥ m;
3) довести, що правильним є твердження Т(k+1);
4)зробити висновок, що згідно узагальненого принципу математичної індукції твердження Т(n) правильне при всіх натуральних значеннях n ≥ m.
Приклад 2.4.
Знайти добуток 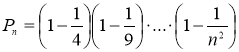 , n ≥ 2.
, n ≥ 2.
Розв’язання.
Розглянемо спочатку такі добутки:
![]()

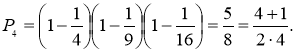
Робимо індуктивне припущення, що ![]() .
.
Доведемо формулу узагальненим методом математичної індукції.
1) Якщо n = 2, то ![]() .
.
2) Нехай твердження правильне при n = k (k ≥2), тобто

Доведемо, виходячи з цього, що правильним буде твердження:
 тобто
тобто

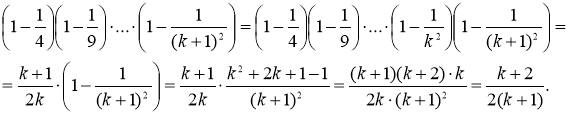
Отже, формула ![]() правильна при всіх натуральних n ≥ 2.
правильна при всіх натуральних n ≥ 2.
Методом математичної індукції доводяться також твердження, правильні при всіх цілих від’ємних числах, а також твердження, правильні на множині цілих чисел, починаючи з деякого цілого m (провівши заміну
n = - m ). В останньому випадку доведення будується на наступному узагальненні принципу математичної індукції.
Деяке твердження Т(n) правильне при всіх цілих n ≥ m, якщо воно:
1) правильне при n = m;
2) із правильності цього твердження при n = k, де k ![]() Z, k ≥ m, слідує, що воно правильне для n = k +1
Z, k ≥ m, слідує, що воно правильне для n = k +1
Доведення проводиться за таким алгоритмом:
- перевірити правильність твердження Т(m);
- припустити, що правильним є твердження T(k), де k ≥ m;
- довести, використовуючи припущення, що правильним є твердження T(k+1);
-
зробити висновок, що твердження T(n) правильне при всіх цілих
n ≥ m.
Приклад 2.5.
Довести, що ![]() при всіх цілих n
при всіх цілих n![]() -1.
-1.
Доведення.
Якщо n = -1, то ![]() .
.
Припустимо, що ![]() ,(k≥ -1).
,(k≥ -1).
Доведемо, що ![]() .
.
![]() .
.
Кожний з доданків ділиться на 16, тому і вся сума ділиться на 16.
Отже, згідно узагальненого принципу математичної індукції
![]() при всіх цілих n
при всіх цілих n![]() -1.
-1.
Приклад 2.6.
Знайти формулу для обчислення суми Sn=![]() .
.
Використаємо неповну індукцію. Розглянемо частинні випадки:
n=1 S1=![]()
![]() n=2 S2=
n=2 S2=![]()
n=3 S3=![]() n=4 S4=
n=4 S4=![]()
Можна зробити припущення, тобто виказати гіпотезу, що Sn=![]() .
.
Доведемо цю формулу методом математичної індукції.
Доведення
1) Базис індукції: При n=1 S1=![]() =
=![]() формула вірна.
формула вірна.
2) Індуктивний перехід:
Припустимо, що дана рівність має місце при n=k, тобто ![]() =
=![]() .
.
Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто, що
Sk+1=![]()
Враховуючи припущення маємо: Sk+1=![]() =
=![]() .
.
Отже формула вірна і при n=k+1. За принципом математичної індукції вона справджується і при будь-якому n![]() .
.
3.2.1 Вправи для самостійної роботи
3.3. Доведення тотожностей і нерівностей методом математичної індукції
Метод математичної індукції дозволяє доводити тотожності і нерівності, одна або обидві частини яких залежать від натурального числа n.
Приклад 3.1.
Довести тотожність при ![]() n
n![]() N.
N.
![]() (2 )
(2 )
Доведення.
При n =1 твердження (2) набуде вигляду:
![]()
![]() .
.
Нехай твердження (2) є тотожністю при n = k, тобто правильною є рівність:
![]()
![]() (3)
(3)
Доведемо, використовуючи це припущення, що тотожністю буде рівність:

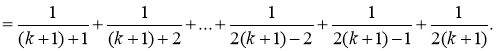 (4)
(4)
Для цього розглянемо різницю лівої та правої частин рівності (4). Якщо різниця буде дорівнювати 0, тоді рівність (4) є правильною. Враховуючи те, що рівність (3) за припущенням – тотожність, різниця лівої та правої частин цієї рівності дорівнює 0. Отже,


![]()
![]()
![]()
![]()
Згідно принципу математичної індукції рівність (2) є тотожністю при ![]() n
n![]() N.
N.
Приклад 3.2.
Довести, що для будь-якого натурального числа n правильною є рівність:
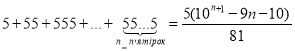 .
.
Доведення.
Якщо n = 1, то ![]() - правильна числова рівність.
- правильна числова рівність.
Припустимо, що правильною є рівність:
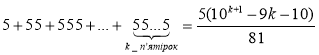 .
.
Звідси 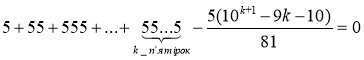 .
.
Доведемо, що правильною буде рівність:
 .
.
Для цього розглянемо різницю лівої та правої частин останньої рівності. Якщо різниця дорівнює 0, то ця рівність правильна.

Згідно принципу математичної індукції рівність:
 правильна при ∀ n
правильна при ∀ n ![]() N.
N.
При доведенні нерівностей використовують властивості нерівностей.
Приклад 3.3.
Довести, що якщо 0 < a < b, то ![]() n
n ![]() N an < bn.
N an < bn.
Доведення.
1) Якщо n =1, то а < b – нерівність, що доводимо, правильна (це випливає з умови).
2) Нехай правильною є нерівність ak < bk. Так як a > 0 i b > 0, то можна помножити нерівність ak < bk на нерівність а < b і отримаємо правильну нерівність ak+1 < bk+1.
Згідно принципу математичної індукції an < bn, ![]() n
n ![]() N.
N.
Приклад 3.4.
Якщо х > -1, то ![]() n
n ![]() N
N
(1 + х)n ≥ 1 + nх (нерівність Бернуллі) (7) Доведення.
Для доведення цієї нерівності застосуємо метод математичної індукції.
Доведення.
1) Якщо n = 1, то маємо (1 + х)1 ≥ 1 + х. Ця нерівність правильна.
2) Нехай (1 + х)k ≥ 1 + kx – правильна нерівність.
Так як 1 + х > 0, то помноживши попередню нерівність на 1 + х, отримаємо правильну нерівність: (1 + х)k+1 ≥ (1 + kх)(1 + х);
(1 + х)k+1 ≥ 1 + (k +1)х + kх2.
Так як kх2 ≥ 0, то звідси слідує
(1 + х)k+1 ≥ 1 + (k +1)х.
Згідно принципу математичної індукції робимо висновок, що нерівність (7) правильна при ![]() n
n ![]() N.
N.
Приклад 3.5.
Довести, що для всіх невід’ємних чисел а і b і натурального числа n:
 . (8)
. (8)
Доведення.
1) При n = 1 ![]() . Ця нерівність правильна.
. Ця нерівність правильна.
2) Нехай нерівність (8) правильна при n = k, тобто
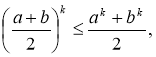
тоді для ![]() а ≥ 0 та b ≥ 0 буде правильною нерівність:
а ≥ 0 та b ≥ 0 буде правильною нерівність:
 (9)
(9)
Враховуючи припущення 1, 2 доведемо, використовуючи це припущення, що правильною буде нерівність:
 . (10)
. (10)
Для цього доведемо нерівність ![]() .
.
![]()
![]()
![]() ,
,
для ![]() а ≥ 0 та b ≥ 0.
а ≥ 0 та b ≥ 0.
Враховуючи нерівності (9) та (10), робимо висновок, що правильною буде нерівність:

Згідно принципу математичної індукції нерівність (8) правильна при![]() n
n ![]() N
N
Приклад 3.6.
Довести, що середнє арифметичне будь-яких n невід’ємних чисел а1, а2, а3, ..., аn не менше їх середнього геометричного, тобто:
![]() (нерівність Коші).
(нерівність Коші).
Доведення.
Якщо n = 2, то ![]() - правильна нерівність, бо
- правильна нерівність, бо
 .
.
Припустимо, що нерівність, яку доводимо, правильна для довільних k невід’ємних чисел, тобто:
![]() .
.
Доведемо, що правильною буде нерівність:
![]() .
.
Переставляючи числа а1, а2, а3, ..., аk , можна досягти того, що число
аk+1 буде найбільшим числом (або одним з найбільших), тобто:
аk+1 ![]() а1;
а1;
аk+1 ![]() а2;
а2;
...
аk+1 ![]() аk.
аk.
Додавши отримані нерівності, матимемо:
k·аk+1 ![]() а1+ а2+ а3+ ...+ аk .
а1+ а2+ а3+ ...+ аk .
Звідси ![]() .
.
Введемо позначення ![]() ,
,
![]() .
.
![]() .
.
Так як ![]() , то
, то ![]() ,
, ![]() .
.
Тому ![]() ,
,
![]() .
.
Піднесемо до (k+1)-го степеня останню рівність:
![]()
![]()
![]() .
.
Але за припущенням ![]() , тому
, тому
![]() .
.
Звідси ![]() .
.
Згідно принципу математичної індукції:
![]() - правильна нерівність для будь-яких невід’ємних чисел а1, а2, а3, ..., аn , n
- правильна нерівність для будь-яких невід’ємних чисел а1, а2, а3, ..., аn , n ![]() N, n
N, n ![]() 2.
2.
Приклад 3.7.
Довести, що ∀ х > 0 і n![]() N має місце нерівність:
N має місце нерівність:
![]() .
.
Доведення.
а) Якщо n = 1, то початкова нерівність набуває вигляду ![]() .
.
Це правильна нерівність, оскільки ![]() .
.
б) Якщо n = 2, то початкова нерівність набуває вигляду:
![]() .
.
Нерівність ![]() правильна при ∀ х > 0, значить, вона правильна і при заміні х на х2, тобто
правильна при ∀ х > 0, значить, вона правильна і при заміні х на х2, тобто ![]() .
.
Додавши до кожної частини останньої нерівності 1, отримаємо:
![]() .
.
в) Припустимо, що правильною є нерівність:
![]() , (11)
, (11)
де k – довільне натуральне число.
Доведемо, що правильною буде нерівність:
![]() .
.
Замінимо в нерівності ![]() вираз х на вираз хk+2 .
вираз х на вираз хk+2 .
Тоді ![]() . (12)
. (12)
Додамо почленно нерівності (11) та (12).
Отримаємо:
![]() .
.
Отже, результати кроків а) та в) дають можливість зробити висновок про те, що початкова нерівність правильна для будь-якого непарного значення n, так само як і ця нерівність буде правильною і для будь-якого парного числа n згідно пунктів б) та в).
В цілому, згідно принципу математичної індукції можна зробити висновок про те, що нерівність:
![]() правильна ∀ х > 0 і n
правильна ∀ х > 0 і n![]() N.
N.
Приклад 3.8.
Довести, що для будь-якого натурального числа n > 1 правильною є нерівність:
![]() .
.
Доведення.
При n = 2 ![]() - правильна числова нерівність.
- правильна числова нерівність.
Дійсно, ![]() .
.
Припустимо, що нерівність ![]() (13)
(13)
є правильною.
Доведемо, що ![]() . (14)
. (14)
Для ∀k![]() 0 має місце нерівність:
0 має місце нерівність:
![]() . (15)
. (15)
Дійсно, ![]() - правильна нерівність.
- правильна нерівність.
Додамо до обох частин цієї нерівності 1.
![]() ;
;
![]()
![]() ·
· ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отже, нерівність (15) правильна.
Додамо почленно нерівності (13) і (15).
![]() ;
;
![]() .
.
Згідно принципу математичної індукції нерівність
![]()
правильна для будь-якого натурального n > 1.
Приклад 3.9
Довести, що для довільного натурального числа ![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. При ![]() отримуємо нерівність
отримуємо нерівність ![]() , яка вірна. Нехай вона вірна при деякому натуральному числі
, яка вірна. Нехай вона вірна при деякому натуральному числі ![]() , тобто виконується нерівність
, тобто виконується нерівність ![]() . Користуючись цим припущенням, покажемо, що вірною є також нерівність
. Користуючись цим припущенням, покажемо, що вірною є також нерівність ![]() . Дістаємо
. Дістаємо
![]()
![]() .
.
Перший доданок одержаного виразу додатний за індуктивним припущенням. Оцінимо суму інших доданків, тобто вираз ![]() . Функція
. Функція ![]() має похідну
має похідну ![]() та екстремуми у точках
та екстремуми у точках ![]() , і, очевидно, зростає на проміжку
, і, очевидно, зростає на проміжку ![]() . Переконавшись, що
. Переконавшись, що ![]() , можемо стверджувати, що при
, можемо стверджувати, що при ![]() виконується нерівність
виконується нерівність ![]() . Посилання на принцип математичної індукції завершує доведення.
. Посилання на принцип математичної індукції завершує доведення.
Приклад 3.10
Довести, що ![]() для всіх натуральних
для всіх натуральних ![]() .
.
Розв’язання.
При ![]() отримуємо нерівність
отримуємо нерівність ![]() , яка вірна. Нехай вона вірна при деякому натуральному числі
, яка вірна. Нехай вона вірна при деякому натуральному числі ![]() , тобто виконується нерівність
, тобто виконується нерівність ![]() . Користуючись цим припущенням, покажемо, що вірною є також нерівність
. Користуючись цим припущенням, покажемо, що вірною є також нерівність ![]() . Маємо
. Маємо
![]() ,
,
оскільки ![]() при
при ![]() . На основі принципу математичної індукції стверджуємо, що задана в умові нерівність вірна.
. На основі принципу математичної індукції стверджуємо, що задана в умові нерівність вірна.
Приклад 3.11
Довести, що для довільного натурального числа ![]() виконується нерівність
виконується нерівність
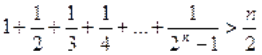 .
.
Доведення. При ![]() отримуємо вірну нерівність
отримуємо вірну нерівність 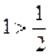 . Нехай вона вірна при деякому натуральному числі
. Нехай вона вірна при деякому натуральному числі ![]() , тобто нехай виконується нерівність
, тобто нехай виконується нерівність
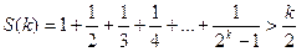 .
.
Використовуючи це припущення, покажемо, що вірною є також нерівність
![]() .
.
Очевидно, що ![]() , де
, де ![]() . Вираз
. Вираз ![]() являє собою суму
являє собою суму ![]() дробів, кожний з яких більший, ніж
дробів, кожний з яких більший, ніж ![]() . Отже,
. Отже,
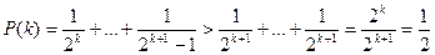 .
.
Таким чином, ![]() (за припущенням) і
(за припущенням) і ![]() . Тому
. Тому ![]() , тобто
, тобто ![]() . На основі принципу математичної індукції стверджуємо що задана в умові нерівність виконується для довільного натурального числа
. На основі принципу математичної індукції стверджуємо що задана в умові нерівність виконується для довільного натурального числа ![]() .
.
Приклад 3.12
Довести, що для довільного натурального числа ![]() та для довільних дійсних чисел
та для довільних дійсних чисел ![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення.
При ![]() нерівність
нерівність ![]() вірна. Справді, вона вірна у випадку, коли одне з чисел (або обидва) рівні 0. У випадку, коли обидва числа додатні або обидва від’ємні, виконується знак рівності. Якщо ж числа різних знаків, то дістаємо строгу нерівність. Можливі і інші доведення цього факту, наприклад, аналітичним методом або методом доведення від супротивного.
вірна. Справді, вона вірна у випадку, коли одне з чисел (або обидва) рівні 0. У випадку, коли обидва числа додатні або обидва від’ємні, виконується знак рівності. Якщо ж числа різних знаків, то дістаємо строгу нерівність. Можливі і інші доведення цього факту, наприклад, аналітичним методом або методом доведення від супротивного.
Нехай нерівність вірна при деякому натуральному ![]() , тобто виконується співвідношення
, тобто виконується співвідношення ![]() . Тоді
. Тоді
![]()
![]() ,
,
що, згідно з принципом математичної індукції, завершує доведення.
Приклад 3.13
Довести, що для ![]() при всіх натуральних
при всіх натуральних ![]() виконується нерівність
виконується нерівність ![]() (нерівність Бернуллі).
(нерівність Бернуллі).
Доведення.
При ![]() виконується знак рівності, тому твердження вірне. Нехай виконується нерівність
виконується знак рівності, тому твердження вірне. Нехай виконується нерівність ![]() . Тоді
. Тоді
![]()
і, відповідно до принципу математичної індукції, нерівність вірна.
Приклад 3.14
Довести методом математичної індукції, що при ![]()
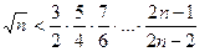 .
.
Доведення. При ![]() отримуємо вірну числову нерівність
отримуємо вірну числову нерівність 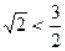 . Припустимо, що вірна нерівність
. Припустимо, що вірна нерівність ![]() і покажемо, що
і покажемо, що
![]() .
.
Із припущення маємо ![]() . Покажемо, що
. Покажемо, що ![]() . Аналізуючи різницю квадратів лівої та правої частин, дістаємо
. Аналізуючи різницю квадратів лівої та правої частин, дістаємо 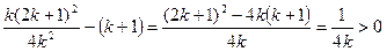 , що доводить потрібне твердження. Отже, відповідно до принципу математичної індукції, нерівність доведена.
, що доводить потрібне твердження. Отже, відповідно до принципу математичної індукції, нерівність доведена.

3.3.1. Вправи для самостійної роботи
3.4. Застосування методу математичної індукції
при розв’язуванні геометричних задач
Приклад 4.1.
Довести, що якщо а та b – катети, с – гіпотенуза прямокутного трикутника, то для всіх натуральних n ![]() 2 має місце нерівність:
2 має місце нерівність:
![]() .
.
Доведення.
Якщо n = 2, то ![]() - правильна нерівність (бо виконується рівність
- правильна нерівність (бо виконується рівність ![]() , що виражає теорему Піфагора).
, що виражає теорему Піфагора).
Припустимо, що правильною є нерівність: ![]() .
.
Доведемо, що правильною буде нерівність ![]() .
.
Так як а та b – катети, с – гіпотенуза прямокутного трикутника, то
a < c, b < c.
Звідси ![]() ,
, ![]() .
.
Додамо останні дві нерівності ![]() .
.
![]() .
.
Згідно принципу математичної індукції робимо висновок про те, що нерівність ![]() правильна ∀ n
правильна ∀ n ![]() 2, n
2, n ![]() N; а, b – катети, с – гіпотенуза прямокутного трикутника.
N; а, b – катети, с – гіпотенуза прямокутного трикутника.
Приклад 4.2.
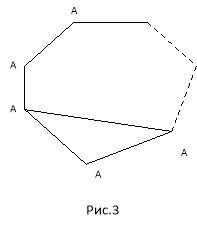
Довести, що сума Sn внутрішніх кутів будь-якого опуклого багатокутника (рис.3) дорівнює 1800⋅(n – 2), де n – число сторін цього багатокутника.
Sn = 1800 ⋅ (n – 2) ![]() (16)
(16)
Доведення.
Це твердження має зміст не для всіх натуральних n, а лише для n ≥ 3.
1) Якщо n = 3, то S3 =1800 ⋅ (3 – 2) = 1800.
Сума внутрішніх кутів будь-якого трикутника дійсно дорівнює 1800.
2) Нехай правильною є формула
Sk =1800 ⋅ (k – 2), k ≥ 3
Доведемо, що буде правильною і формула Sk+1 =1800 ⋅(k + 1 – 2).
Нехай А1А2…АkAk+1 – довільний опуклий (k +1)-кутник. Сполучивши точки А1 і А2, ми отримаємо опуклий k – кутник А1А2…Аk-1Ak. Очевидно, що сума кутів k+1-кутника А1А2…АkAk+1 дорівнює сумі кутів k-кутника А1А2…Аk плюс сума кутів ∆А1АkAk+1. Але сума кутів k-кутника А1А2…Аk за припущенням рівна 1800⋅(k – 2), а сума кутів ∆А1АkAk+1 дорівнює 1800. Тому Sk+1 = Sk + 1800 =1800 ⋅ (k –2) + 1800 =1800 ⋅ (k – 1).
Отже, згідно принципу математичної індукції формула (16) правильна при будь-якому натуральному n ≥ 3.
У площині проведено n прямих, із яких ніякі дві не паралельні і ніякі три не проходять через одну точку. На скільки частин розбивають площину ці прямі ?
Розв’язання.
Зробивши відповідні рисунки, можна легко переконатися в тому, що одна пряма розбиває площину на 2 частини, дві прямі – на 4 частини, три прямі – на 7 частин, чотири прямі – на 11 частин.
Позначимо через N(n) – число частин, на які n прямих розбивають площину. Тоді :
N (1) = 2;
N (2) = N (1) + 2;
N (3) = N (2) + 3;
N (4) = N (3) + 4.
Можна припустити, що N (n) = N (n –1) + n.
Складемо почленно ці n рівностей:
N (n) = 2 + 2 + 3 + 4 + …+ n, або
![]() .
.
Доведемо правильність останньої формули за допомогою методу математичної індукції.
1) Якщо n = 1, то N (1) = 2.
2) Припустимо, що формула правильна при n = k, тобто
![]() .
.
Розглянемо k +1 прямих. Виділимо з них довільним чином k прямих. За припущенням індукції вони розбивають площину на ![]() частин.
частин.
k+1-ша – пряма, що залишилася, розіб’ється виділеними k прямими на k +1 частин і, відповідно, пройде по k +1 частинах, на які площина була вже розбита, і кожну з цих частин розділить на 2 частини, тобто додається ще
k + 1 частина.
Отже,
![]() ,
,
що й потрібно було довести.
Таким чином, формула ![]() правильна при
правильна при ![]() n
n ![]() N.
N.
3.4.1. Вправи для самостійної роботи
3.5. Застосування методу математичної індукції
при розв’язуванні задач, пов’язаних з рекурентним способом задання послідовностей.
Означення.
Формула, яка виражає кожний член послідовності через один або кілька попередніх членів, називається рекурентною формулою.
Наприклад, аn = 3аn-2 – 2аn-1.
При рекурентному способі задання послідовності задають:
а) один або кілька перших членів послідовності;
б) рекурентну формулу.
Наприклад, а1 = 3, а2 = -1, аn = (-1)n аn-1 – 2аn .
Приклад 5.1.
Послідовність Фібоначчі задається наступними умовами:
а0 = 0, а1 = 1, …, аn+1 = аn + аn-1.
Довести, що:
![]() . (17)
. (17)
Доведення.
1) З умови маємо, що а2 = 1, а3 = 2, а4 = 3.
Якщо n = 1, то а2⋅а3 – а1⋅а4 = 1⋅2 - 1⋅3 = (-1)1.
2) Нехай рівність (17) правильна при n = k, k ∈ N:
ak+1⋅ak+2 - ak⋅ak+3 = (-1)k.
При n = k + 1 маємо:
ak+2 ⋅ ak+3 – ak+1 ⋅ ak+4 = ak+2 ⋅ ak+3 – ak+1 (ak+3 + ak+2) =
= ak+2 ⋅ ak+3 – ak+1 ⋅ ak+3 – ak+1 ⋅ ak+2 =
= (ak+1 + ak) ak+3 - ak+1 ⋅ ak+3 - ak+1 ⋅ ak+2 =
= ak+1 ⋅ ak+3 + ak ⋅ ak+3 - ak+1 ⋅ ak+3 - ak+1 ⋅ ak+2 = -( ak+1 ⋅ ak+2 - ak ⋅ ak+3) =
= -(-1)k = (-1)k+1.
Отже, формула (17) правильна згідно принципу математичної індукції при ![]() n
n ![]() N.
N.
3.5.1. Вправи для самостійної роботи
3.6. Застосування методу математичної індукції при виведенні формули n-го члена і суми перших n членів
арифметичної і геометричної прогресій.
Приклад 6.1.
Вивести формулу n-го члена арифметичної прогресії.
Розв’язання.
a2 = a1 + d, a3 = a2 + d = a1 + 2d, a4 = a3 + d = a1 + 3d.
Ці рівності дають можливість припустити, що для ![]() n
n ![]() N правильною буде рівність: an = a1 + (n – 1)d.
N правильною буде рівність: an = a1 + (n – 1)d.
Доведемо її за допомогою методу математичної індукції:
1) Якщо n = 1, то а1 = а1.
2) Нехай ak = a1 + (k – 1)d – правильна рівність.
Тоді ak+1 = ak + d = a1 + (k – 1)d + d = a1 + ((k + 1) – 1) d.
Отже, згідно принципу математичної індукції робимо висновок про правильність формули an = a1 + (n – 1)d, при ![]() n
n ![]() N.
N.
Приклад 6.2.
Довести, що формула n-го члена геометричної прогресії має вигляд:
bn = b1 ⋅ qn-1.
Доведення.
1) Якщо n = 1, то b1 = b1.
2) Нехай bk = b1 ⋅ qk-1 – правильна рівність.
Тоді bk+1 = bk ⋅ q = b1 ⋅ qk-1⋅q = b1⋅qk-1+1 = b1⋅q(k+1)-1.
Згідно принципу математичної індукції рівність bn = b1 ⋅ qn-1 правильна при ![]() n
n ![]() N.
N.
Приклад 6.3.
Вивести формулу для знаходження суми n перших членів арифметичної прогресії.
Розв’язання.
Sn = a1 + a2 + …+an = a1 + (a1 + d) + …+(a1 + (n –1)d) =
= na1 + d(1 + 2 + …+(n – 1)).
Таким чином, виведемо формулу для знаходження суми
1 + 2 + …+ (n – 1) перших n –1 натуральних чисел. Позначимо суму перших n натуральних чисел через sn. На основі результатів, отриманих у прикладі 4.1:
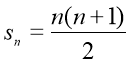 .
.
Оскільки s1 = 1, a  при n =1 також дорівнює 1, то наше припущення правильне при n =1.
при n =1 також дорівнює 1, то наше припущення правильне при n =1.
Нехай воно правильне при k, тобто правильною є рівність:
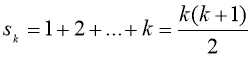 .
.
Тоді

Згідно принципу математичної індукції формула ![]() правильна при
правильна при ![]() n
n ![]() N.
N.
![]() а тому
а тому
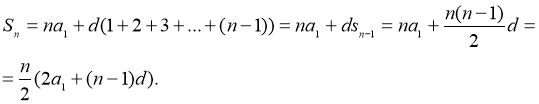
Так як ![]() то
то

Приклад 6.4.
{bn} – геометрична прогресія із знаменником q (q≠1), Sn – сума перших n її членів. Довести методом математичної індукції, що 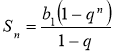 .
.
Доведення.
Зазначимо, що ![]() .
.
Якщо n = 1, то ![]() - правильна рівність.
- правильна рівність.
Припустимо, що  .
.
З іншого боку ![]() , тобто згідно припущення правильною буде рівність
, тобто згідно припущення правильною буде рівність 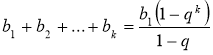 .
.
Отже,  .
.
Доведемо, що 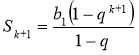 .
.
Тобто потрібно довести, що:
 .
.
Для цього розглянемо різницю лівої та правої частин останньої рівності. Якщо різниця дорівнює 0, то рівність правильна.
![]()
Зазначимо, що ![]() (згідно формули n-го члена геометричної прогресії).
(згідно формули n-го члена геометричної прогресії).
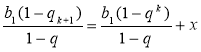 .
.
Звідси 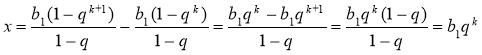 .
.
Тобто 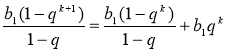 .
.
Отже, згідно принципу математичної індукції формула 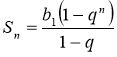 правильна ∀n
правильна ∀n![]() N.
N.
3.6.1. Вправи для 
самостійної роботи
3.7. Застосування методу математичної індукції в тригонометрії
Приклад 7.1.
Довести, що для будь-якого натурального n має місце нерівність:
![]() .
.
Доведення.
Якщо n = 1, то ![]() - правильна нерівність, оскільки виконується умова
- правильна нерівність, оскільки виконується умова ![]() .
.
Нехай правильною є нерівність:
![]() .
.
Доведемо, що правильною буде нерівність:
![]() .
.
![]() .
.
Отже, згідно принципу математичної індукції:
![]() , ∀ n
, ∀ n ![]() N.
N.
Примітка.
![]() , тому 0
, тому 0 ![]()
![]() , отже,
, отже, ![]() .
.
![]() , тому 0
, тому 0![]()
![]() , отже,
, отже, ![]()
Приклад 7.2.
Довести, що для цілих n![]() 0 має місце нерівність:
0 має місце нерівність: ![]() .
.
Доведення.
Застосуємо для доведення цієї нерівності узагальнений метод математичної індукції.
Якщо n = 0, то ![]() , 0
, 0 ![]() 0 – правильна числова нерівність.
0 – правильна числова нерівність.
Припустимо, що правильною є нерівність: ![]() .
.
Доведемо, що правильною буде нерівність ![]() .
.
![]()
![]()
![]() .
.
Отже, згідно узагальненого принципу математичної індукції нерівність
![]() правильна при будь-яких цілих n
правильна при будь-яких цілих n![]() 0.
0.
Приклад 7.3.
Довести тотожність:
![]() .
.
Доведення.
1. Якщо n = 1, то
 ,
, ![]() - правильна рівність.
- правильна рівність.
2. Припустимо, що правильною є рівність
![]() .
.
3. Доведемо, що правильною буде рівність:
 .
.
Розглянемо різницю лівої та правої частин цієї рівності:
![]()
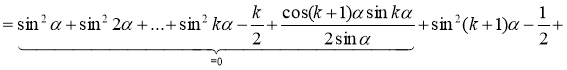
![]()
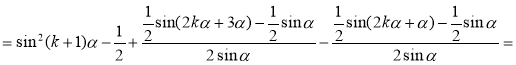
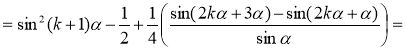
![]()
![]() .
.
4. Згідно принципу математичної індукції початкова рівність правильна ∀ n![]() N, тобто є тотожністю.
N, тобто є тотожністю.
Приклад 7.4.
Довести, що якщо ![]() , де
, де ![]() , то правильною є нерівність:
, то правильною є нерівність:
![]() , ∀n
, ∀n![]() N.
N.
Доведення.
Якщо n = 2, то, враховуючи, що ![]() і
і ![]() , маємо
, маємо
 .
.
Припустимо, що нерівність, яку доводимо, правильна для числа
n = 2k. Доведемо, що вона буде правильною і для числа 2n = 2k+1.
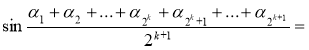

![]()
Отже, згідно принципу математичної індукції робимо висновок, що нерівність, яку доводимо, правильна для чисел виду n = 2k, тобто для n = 2, 4, 8, … і взагалі для будь-якого n, яке є степенем 2. В розглянутому випадку була застосована індукція «вгору».
Для того, щоб довести, що початкова нерівність правильна для будь-якого натурального n, застосуємо індукцію «вниз».
Припустимо, що нерівність, яку доводимо, правильна при деякому значенні n. Доведемо, що тоді вона буде правильною і при n -1.
Таким чином,
 - правильна нерівність. (18)
- правильна нерівність. (18)
Доведемо, що правильною буде нерівність:
 .
.
Розглянемо наступні перетворення:
![]()
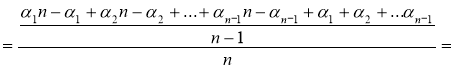
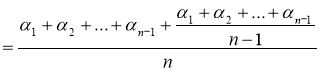 .
.
Нехай  .
.
Оскільки ![]() , то
, то  .
.
Тоді ![]() . (19)
. (19)
З нерівності (18) маємо:

 .
.
Враховуючи (19) маємо:
 .
.
Звідси:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким чином, виходячи з припущення, що початкова нерівність правильна для числа n ми довели, що вона правильна і для числа n – 1. В поєднанні з результатом, отриманим для степенів 2, ми одержали індуктивне доведення початкової нерівності. Запропоновану в даній вправі індукцію «вгору-вниз» можна було б використати і в інших раніше розглянутих вправах (наприклад при доведенні нерівності Коші.
3.7.1. Вправи для самостійної роботи
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Каганов Е.Д. 400 найцікавіших задач з рішеннями по шкільному курсу математики для 6-11 класів. - М. - ЮНВЕС. - 1997. - 288 с.
2. Мовчан С.М., Метод математичної індукції в шкільному курсі математики. Київ - 2013
3. Галицкий М.Л. и др., Сборник задач по алгебре для 8-9 кл. – М.: Просвещение, 1997.
4.Шевченко А.В “Математична індукція”. Київ, 1996
5. Сарана О.А. Математичні олімпіади: просте і складне поруч: Навч. посібн. - К.: Видавництво А.С.К., 2008.-344с.
6. http://ur.co.ua/53/928-1-metod-matematicheskoiy-indukcii.html
![]()
1


про публікацію авторської розробки
Додати розробку
