Робота "Використання ключових компетентностей учнів на основі інноваційних освітніх технологій при формуванні пізнавальної активності молодших школярів"
Автор- упорядник:
Андрушок Олена Миколаївна, вчитель початкових класів, спеціаліст вищої категорії.
«Використання ключових компетентностей учнів на основі інноваційних освітніх технологій при формуванні пізнавальної активності молодших школярів».
Успішне вирішення проблем школи неможливе без використання педагогічної діяльності сучасних досягнень педагогіки. Пошук і розробка активних методів навчання є характерним для всієї сучасної педагогіки. Одним з таких активних групових методів, мета яких – виробити в учнів комунікативні навички, є різні види ігор. Цей метод без перебільшення, - найпопулярніший і найзатребованіший різновид роботи з дітьми. Виходячи з основних цілей та завдань сучасного освітнього процесу в Україні, вчитель розглядає і обґрунтовує доцільність використання інноваційних методик початкової школи. вчитель розкриває переваги методики і її практичні результати. Показує використання різних методів навчальних, що урізноманітнює навчальний процес і сприяє співпраці вчителя та учня.
Робота призначена для вчителів початкових класів.
З М І С Т
Вступ……………………………………………………………………… 4
І Теорія ігрової діяльності………………………………………………. 8
1.1. Особливості гри як діяльності учнів……………………………… 14
1.2. Сюжетно-рольові ігри, дидактичні розвиваючі ігри…………….. 23
1.3. Розвиток у грі творчих здібностей учнів…………………………. 28
Висновок…………………………………………………………………. 34
Список використаної літератури................................................................ 36
Додатки………………………………………………………………….. 37
Дидактичні матеріали………………………………………………….. 38
Додаток 1 ………………………………………………………………..38
Додаток 2 …………………………………………………………………90
ВСТУП
Соціальні перетворення в українському суспільстві докорінно змінили орієнтації в галузі освіти. Нова освітня філософія визначила головну стратегію педагогічної діяльності: спрямування навчально-виховного процесу на формування духовного світу особистості; утвердження загальнолюдських цінностей, розкриття потенційних можливостей та здібностей учнів.
Розв’язання цих актуальних проблем можливо лише на основі широкого запровадження нових педагогічних технологій, спрямованих на всебічний розвиток дитини.
Одним із основних методичних інновацій є інтерактивні методи навчання. Слово “інтерактив” прийшло до нас із англійської мови “interact”, “Inter” – це “взаємний”, “act” – діяти. Інтерактивне навчання – діалогове навчання, в ході якого здійснюється взаємодія вчителя і учня.
Мета інтерактивного навчання – створювання комфортних умов навчання при яких учень відчуває свою успішність, свою інтелектуальну досконалість, що робить продуктивним сам освітній процес.
Тому мета введених на сучасному етапі інтерактивних методів навчання полягає у тому, щоб навчальний процес відбувався за умови постійної, активної взаємодії всіх учнів. Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор і спільне вирішення проблеми на основі аналізу обставин та відповідної ситуації. Воно ефективно сприяє формуванню навичок і вмінь, виробленню цінностей, створенню атмосфери співробітництва, взаємодії, дає змогу педагогу стати справжнім лідером дитячого колективу.
Інтерактивна взаємодія включає як домінування одного учасника навчального процесу над іншим, так і однієї думки над іншою. Під час інтерактивного навчання учні вчаться бути демократичними, спілкуватися з іншими людьми, конструктивно мислити, приймати продуктивні рішення.
Суть інтерактивного навчання полягає у тому, що навчальний процес відбувається за умови постійної, активної взаємодії всіх учнів. Це співнавчання, взаємонавчання (колективне групове навчання у співпраці) де і учень, і учитель є рівноправними, рівнозначними суб’єктами навчання, розуміють, що вони роблять, рефлектують з приводу того, що вони знають, вміють і здійснюють.
Інтерактивне навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне вирішення проблеми на основі аналізу обставин та відповідної ситуації. Воно ефективно сприяє формуванню навичок і вмінь, виробленню цінностей, створенню атмосфери співпраці, взаємодії, дає змогу вчителю стати лідером колективу.
Такі підходи до навчання не є абсолютно новими для української школи. Частково вони використовувалися в перші десятиріччя минулого століття і були поширені в педагогіці на практиці української школи в 20-ті роки – роки масштабного реформування шкільної освіти. Природно-лабораторний та проектний методи, робота в парах змінного складу, виробничі та трудові екскурсії й практики були передовим словом не лише в радянській але й у сучасній педагогіці. Застосування цих методів та форм навчання в окремих школах давало разючі результати.
Подальшу розробку елементів і.н. ми можемо знайти в працях В.Сухомлинського, творчості вчителів-новаторів 70-80-х років. Ш.Амонашвілі, В.Шаталова, Є.Ільїна, С.Лисенкової та інших, теорії розвивального навчання.
У Західній Європі та США групові форми навчальної діяльності учнів активно розвивались та вдосконалювались. Наприкінці ХХ ст. інтерактивні технології набули поширення в теорії та практиці американської школи, де їх використовують у викладанні різних предметів. Дослідження, проведені Національним тренінговим центром (США, штат Мері Ленд) у 80-х рр.., показують, що інтерактивне навчання дає змогу збільшити відсоток засвоєння матеріалу, оскільки впливає не лише на свідомість учня, а й на його почуття, волю.
Вчені зробили висновок, що найгірші результати забезпечує пасивне навчання (лекція – 5%, читання – 10%), а найкращі – інтерактивне (дискусійні групи – 50%. Практика через дію – 75%, навчання інших чи негайне застосування – 90%).
Ці дані цілком підтверджують дослідження сучасних російських психологів. За їхніми оцінками, старший школяр може, читаючи очима, запам’ятовувати 10% інформації, слухаючи – 26%, розглядаючи – слухаючи і розглядаючи – 50%, обговорюючи – 70%, через особистий досвід – 80%, спільну діяльність з обговоренням – 90%, навчання інших – 95%.
Чим зумовлені такі результати? Щоб зрозуміти цей механізм, пригадаємо, як працює наш мозок. Інформація, яка поступає до нього. Не просто записується, а й аналізується, обробляється. Наш мозок схожий на комп’ютер, а ми його користувачі. Щоб комп’ютер працював, його потрібно ввімкнути. Так само потрібно “ввімкнути” і мозок учня. Коли навчання пасивне, мозок не вмикається. Комп’ютер потребує правильного програмування, щоб інтерпретувати дані, введені в його пам’ять. Наш мозок повинен пов’язати те, що нам вкладають, з тим, що ми вже знаємо і як ми думаємо. Коли навчання пасивне він не простежує ці зв’язки і не забезпечує інформацією.
Нарешті, наш мозок повинен перевірити інформацію, узагальнити її, пояснити комусь для того, щоб зберегти її в банку пам’яті. Коли навчання пасивне, мозок не зберігає інформацію в банку пам’яті.
Використання наочності збільшує запам’ятовування матеріалу від 14 до 38%. Наочність варта не тільки сотень слів, а й утричі ефективніша за одні лише слова.
Якщо до роботи залучається слухова й зорова пам’ять, є більше шансів задовольнити потреби різних учнів, чий спосіб сприйняття матеріалу може суттєво відрізнятися.
Однак використання лише зорової та слухової пам’яті недостатнє. Понад дві тисячі років тому видатний китайський педагог Конфуцій сказав:
Те, що я чую, я забуваю.
Те, що я бачу, я пам’ятаю.
Те, що я роблю, я розумію.
Ці три прості твердження обґрунтовують необхідність використання активних методів навчання. Дещо змінивши слова видатного педагога, можна сформулювати кредо і.н.:
Те, що я чую, я забуваю.
Те, що я бачу, я трохи пам’ятаю.
Те, що я чую, бачу й обговорюю, я починаю розуміти.
Те, що я чую, бачу, обговорюю й роблю я набуваю знань і навичок.
Коли я передаю знання іншим, я стаю майстром.
Процес навчання – не автоматичне викладання навчального матеріалу в голову учня. Він потребує напруженої розумової роботи дитини і її власної активної участі в цьому процесі. Пояснення й демонстрування, самі по собі, ніколи не дадуть справжніх стійких знань. Цього можна досягти тільки за допомогою активного (інтерактивного навчання).
Розвиток науки і техніки дав учителям та учням нові форми комунікації, нові типи розв’язання абстрактних і конкретних завдань, перетворюючи вчителя з авторитетного транслятора готових ідей у натхненника інтелектуального та творчого потенціалу учня. Будь-яка педагогічна технологія повинна відповідати основним критеріям технологічності: системності (наявність логіки процесу, взаємозв’язку частин, цілісність), керованість (можливість діагностики досягнення цілей, планування процесу навчання), ефективності (технологія повинна вибиратися відповідно до результатів і оптимальних затрат, гарантувати досягнення певного стандарту навчання), відтворюваності (можливості застосування в інших однотипних навчальних закладах іншими суб’єктами).
Інтерактивна технологія навчання – це така організація навчального процесу за якої неможлива неучасть школяра в колективному, взаємодоповнюючому, заснованому на взаємодії всіх його учасників процесі навчального пізнання: або кожен учень має конкретне завдання, за яке він повинен публічно прозвітуватись, або від його діяльності залежить якість виконання поставленого перед групою чи перед усім класом завдання. Інтерактивна технологія навчання охоплює чітко спланований очікуваний результат навчання, окремі інтерактивні методи й прийоми, що стимулюють процес пізнання, розумові та навчальні умови й процедури, за допомогою яких можна досягти запланованих результатів.
І РОЗДІЛ. Теорія ігрової діяльності
Гра багатогранна, вона розвиває, виховував, розважає, соціалізує. Але історично одна з головних її задач – навчання. З моменту свого виникнення гра постає основною формою відтворення реальних життєвих ситуацій, сприяє виробленню необхідних людських рис, якостей, навичок, звичок, розвитку здібностей. Так, у давніх Афінах (VI-IV ст.. до н. е.) процес виховання й навчання здійснювався в дусі змагань: діти постійно змагалися з гімнастики, у танцях, музиці, малюванні, самостверджувались і відшліфовували свої кращі якості. У Західній Європі в епоху Відродження й реформації Т. Кампанелла й Ф. Рабле пропагували принцип ігрового навчання (коли учні в грі опановують основи наук). У XV-XVII ст. Я. А. Коменський закликав усі «школи-майстерні» перетворити на місця ігор. На його думку, навчання в будь-якій школі може стати універсальною грою, яка відповідає віку кожного учня. У своїх трудах гру як особливу форму навчання рекомендували Ж.-Ж. Руссо й Ф. Фрабель.
Поняття «гра» в педагогічній літературі трактується досить по-різному. За Г. Селевком, гра – «це вид діяльності в умовах досвіду, в якому складається та вдосконалюється самоуправління як «спеціально створені ситуації, що моделюють реальність, із яких учням пропонується знайти вихід». У педагогічній енциклопедії читаємо: «Гра – засіб фізичного, розумового та морального виховання дітей».
Дійсно, гра – це складне,багатогранне явище, яке неможливо однозначно трактувати. Навчальна гра може тривати від кількох хвилин до цілого уроку й може використовуватися на різних етапах, а також у позакласній роботі. Будь-яка гра включає три основні етапи:
- підготовчий (формулюється мета гри, відбирається навчальний зміст, розробляється сценарій, готується обладнання, розподіляються ролі, проводиться інструктування тощо);
- безпосереднє проведення гри;
- узагальнення, аналіз результатів.
На відміну від розвивальних, навчальні ігри мають певні істотні характеристики та сталу структуру. До основних взаємопов’язаних компонентів гри належить (за В. Коваленком, П. Підкасистим):
- ігрова задумка;
- правила;
- ігрові дії;
- дидактичні завдання (пізнавальний зміст);
- обладнання;
- результат гри.
Ігрові технології навчання відрізняються від інших технологій тим, що гра:
- добре відома, звична й улюблена форма діяльності для людини
будь –якого віку;
- ефективний засіб активізації. У грі легше долаються труднощі, перешкоди, психологічні бар’єри;
- мотиваційна за своєю природою (по відношення до пізнавальної діяльності вона вимагає від учнів ініціативності, творчого підходу, уяви, цілеспрямованості);
- дозволяє вирішувати питання передачі знань, умінь, навичок;
- багатофункціональна, її вплив на учня неможливо обмежити одним аспектом;
- переважно колективна, групова форма роботи, в основі якої знаходиться змагання. В якості суперника може бути як сам учень (переконання себе, покращення свого результату), так і інший;
-
має кінцевий результат. У грі учасник має отримати приз: матеріальний, моральний (грамота, широке оголошення результату,заохочення
) психологічний (самоствердження, самооцінка; - має чітку поставлену мету й відповідний педагогічний результат (В. Кругляков, 1998).
На практиці в системі активного навчання використовуються такі моделі навчальної гри: імітаційні, операційні, рольові, сюжетні, ігри-змагання.



![]()
![]()

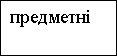

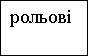





![]()
![]()
![]()








![]()






В імітаційних іграх під час заняття імітується діяльність організацій, подій, конкретна робота людей (журналіст, політик, еколог та ін.), обстановка, умови, в яких відбувається подія. Сценарій імітаційної гри містить сюжет події, опис структури та призначення імітованих об’єктів. Прикладом може бути урок-мандрівка, урок-екскурсія тощо.
Операційні ігри допомагають відпрацювати виконання конкретних специфічних операцій (методику проведення дискусії, конференції, бесіди, диспуту). В операційних іграх моделюється процес діяльності. Вони проходять в умовах, що імітують реальну обстановку (урок-розслідування, урок-суд).
У рольових іграх відпрацьовується тактика поведінки, дій, виконання функції. Між учасниками розподіляються ролі з обов’язковим змістом відповідно до проблемної ситуації, винесеної на обговорення. Для проведення таких ігор доцільно використовувати такі типи нестандартних уроків: урок-КВК,урок-подорож, урок-казка, урок-композиція.
Усі навчальні ігри, активізуючи увагу, підвищуючи інтерес до вивчення предмета, мають спільні вимоги до проведення: коли гра вже почалася, ніхто не має права втручатися й змінювати її хід (лише корегує дії учасників, якщо вони змінюють мету гри), наприкінці кожної гри мета аналізується та обговорюється, констатуються результати, оцінюються (словесно) результати.
Структура розгорнутої ігрової діяльності включає такі компоненти:
- спонукальний (потреби, мотиви, інтереси, прагнення, які визначають бажання брати участь у грі);
- орієнтувальний (вибір засобів і способів ігрової діяльності);
- виконавчий (дії, операції, які надають можливості реалізувати ігрову мету);
- контрольно-оцінювальний (коригування та стимулювання активності в ігровій діяльності).
Чому багато хто з людей незважаючи на вік так любить ігри?
Насамперед, мабуть, тому, що гра –це цілісний стан душі. Добре продумана гра з цікавим сюжетом зачіпає цілий психологічний шар і захоплює людину цілковито. У грі людина може прожити гармонійне життя в іншій подобі, ілюзії, ситуації, досягти єдності думок, почуттів і руху, внаслідок чого настає катарсис – очищення душі, або інсайт – творче осяяння.
Крім того, гра – це унікальний фантастичний простір, що осягає величезний творчий потенціал: можна будувати свої відносини з іншими, своє майбутнє в безпечній атмосфері чи ситуації, можна сказати собі: “я граю роль” – і дозволити бути самим собою. У грі ми більше схожі на себе, ніж у житті, гарна гра – це психологічний експеримент, який проводить сам із собою кожен учасник. Результати цього експерименту не завжди передбачувані, більш того – вони майже завжди несподівані, а іноді – й болісні, тому, якщо учасник не спроможний прийняти й осмислити новий досвід, гра пропонує йому безпечний вихід, захист: “То був не ти, а нав’язана тобі роль”.
Гра надає широкі можливості для розвитку і самопізнання, якщо учень готовий до цього. Гра дозволяє осмислити і зрозуміти своє внутрішнє “я”, побудувати нові моделі поведінки з оточуючими, навчитися інакше ставитися як до себе, так і оточуючих близьких людей, до світу навколо себе. Гра розвиває важливі соціальні навички та вміння, здатність до емпатії та до кооперації, вміння вирішувати конфліктні ситуації через співробітництво, вчить бачити ситуацію очима інших та дозволяє одержати досвід, цінний для власного майбутнього життя її учасників.
Основний принцип теорії ігор полягає в тому, що будь-яке спілкування корисне і вигідне людям. Фізичний контакт сприятливо впливає не тільки на фізичний і емоційний розвиток, але й на біохімію мозку. “Прогладжування” – не тільки фізичний, але й будь-який акт, що припускає визначення присутності іншої людини. Обмін “прогладжуваннями” можна розглядати як соціальну одиницю спілкування.
Як Д.Б. Ельконін відзначає у своїй книзі “Психологія гри”, слова “гра”, “грати”, наприклад, у російській мові багатозначні. Слово “гра” вживається в значенні розваги, у переносному значенні – “гра з вогнем”, “гра на нервах”, чогось незвичайного - “гра природи”, “гра долі” і “гра на музичному інструменті” тощо.
Деякі вихідні дані про ігри містяться в етнографічних джерелах. Початок розробки теорії гри зазвичай пов’язують з іменами таких мислителів ХІХ ст., як Ф.Міллер. М.Спенсер, В.Вундт. Розробляючи свої філософські, психологічні і – головним чином – естетичні погляди, вони розглядали і гру як одне із найпоширеніших явищ життя, пов’язуючи походження гри з походженням мистецтва. Для Ф.Міллера гра є природною діяльністю, а ось надлишок сил, вільних від зовнішніх потреб, є для нього лише передумовою виникнення естетичної насолоди, яку приносить гра. М.Спенсер вважає, що діяльності, які називають іграми, поєднані з естетичними діяльностями однією спільною рисою: жодні з них не можуть безпосередньо бути процесами, які служать життю. Ближче за всіх до розуміння виникнення гри підійшов свого часу В.Вундт. Він схильний вважати джерелом гри насолоду. “Гра – це дитя праці, - писав він. – Немає жодної гри, що не мала б собі прототипу в одній з форм серйозної праці, що завжди передує їй і за часом, і за самою сутністю”.
Інтерес до гри як першої діяльності дитини, виявили ще в 30-ті роки ХХ ст. відомі вітчизняні психологи Л.С.Виготський і Д.Б. Ельконін.
Виникаючи на межі раннього дитинства та дошкільного віку, рольова гра інтенсивно розвивається та досягає в другій половині дошкільного віку свого найвищого рівня. Вивчення розвитку рольової гри цікаве в подвійному сенсі: по-перше, за такого дослідження глибше розкривається сутність гри; по-друге, розкриття взаємозв’язку окремих структурних компонентів гри в їх розвитку може стати у нагоді педагогічному керівництві у формуванні цієї найважливішої діяльності дитини.
Одним із істотних завдань під час дослідження рольової гри є з’ясування питань про психологічні передумови, що стали підґрунтям узяття на себе дитиною ролі, та розвиток змісту ролі, яку виконує дитина в грі. На менш важливим є з’ясування зміни ставлення дитини до виконання ролі у грі. Гра – це така діяльність, у якій відтворюються соціальні відносини між людьми поза умовами утилітарної діяльності.
Змістом розгорнутої, розвиненої рольової гри є не предмет як такий і його використання чи зміна людиною, а відносини між людьми, які здійснюються саме через дії з предметами.
Гра не тільки бере свій сюжет із навколишньої дійсності, але й за своєю природою соціальна, тому що виникає з умов життя в суспільстві. Рольова гра виникає в ході історичного розвитку суспільства як результат зміни місця дитини в системі громадських відносин, таким чином складаючи найголовніший бік дитячого життя. Діти грають з разючою невтомністю, в міру розвитку інтелекту дитини інтерес до гри зростає, гра задовольняє інтереси дитини.
Грою називають і психотехнічний прийом, з допомогою якого за короткий час можна налаштувати дітей на роботу в групі, структуровану дію за правилами, більш складну рольову дію та багато чого іншого. Такими чином, можемо констатувати, що є багато ігор і між ними існують значні розбіжності.
У більшості випадків ігровий прийом у роботі психолога або вчителя виконує допоміжну функцію надійного і перевіреного засобу для реалізації діяльності психолога або вчителя, іноді гра стає для них основною діяльністю: спершу, на етапі продумування та розробки, - діяльністю, яка створює її ведучого, а потім – одночасно діяльністю і ведучого, і учасників (ведучий гри завжди одночасно є її учасником, бо грає “свою гру”.
Гра – це спільна діяльність, що припускає колективну взаємозалежність і розширення особистих можливостей за рахунок залучення потенціалу інших учасників.
Працюючи з шести річками 20 років переконана, що для дітей використовується найсприятливіший період для засвоєння знань, умінь і навичок. Важливо з самого початку зацікавити дитину, тому урок слід починати з ігрового моменту.
Шість років – це вік чомучок, це вік цупкої гострої пам’яті. З якою радістю кожного дня зустрічаюсь зі своїми чомучками, фантазерами! І нехай іноді мені доводиться з ними клопітно, але проникати в їхній дитячий мир, чути їхній задорний сміх – велике вчительське щастя.
Проводячи уроки, зрозуміла, як нелегко передавати знання моїм малюкам. Вони не люблять однакового. Для виконання навчальної діяльності у них ще немає необхідних вмінь і навичок, не розвинена працездатність, посидючість. Навчання вони сприймають як новий, більш серйозний вид гри, з новими правилами і результатами. Але у шести річок є велике бажання вчитися. Прагну складати на кожному уроці таку навчальну ситуацію, яка дозволила б кожній дитині показати себе.
У шестирічної дитини фантазія розвинена настільки, що дозволяє їй проявитися там, куди запрошує гра, отже, дитина приймає ті умови, які ставить перед нею вчитель, організовуючи гру.
- Особливості гри як діяльності учнів
Грі належить велика роль у житті та розвитку дітей молодшого шкільного віку: в ігровій діяльності формуються багато позитивних якостей дитини, інтерес і готовність до майбутнього навчання, розвиваються її пізнавальні здібності. Гра важлива як для підготовки дитини до майбутнього, так і для того, щоб зробити її теперішнє життя повним і щасливим. Гра – це своєрідний спосіб засвоєння громадського досвіду, властивий дітям молодшого шкільного віку. У грі формуються всі сторони особистості дитини, відбуваються значні в її психіці, які готують перехід до нової, більш високої стадії розвитку.
Цим обумовлені величезні виховні можливості гри, яку психологи вважають першочерговою діяльністю молодшого школяра. Гра – відображення життя: тут усе “начебто”, “не насправді”, але в цій умовній обстановці, створеній дитячою уявою, багато реального, справжнього – дії гравців завжди реальні, їх почуття чи переживання справжні та щирі. Наслідування дорослих у грі пов’язане з роботою уяви: дитина не копіює дійсність, вона комбінує різні життєві враження з особистим досвідом. Гра – самостійна діяльність, у якій діти вперше починають спілкуватися з однолітками: їх поєднують спільна мета, спільні зусилля для її досягнення, спільні інтереси та переживання. Саме тому гра привчає дітей підкоряти свої дії та думки певній меті, допомагає виховувати цілеспрямованість: у грі всі сторони дитячої особистості формуються в єдності та взаємодії, у грі формується колектив друзів. Виховуються творчі почуття, організаторські вміння, у грі складаються взаємини. Однак тільки за умови гарної організації шкільного колективу можна успішно розвивати творчі здібності кожної дитини та її активність.
Гра для її учасників є діяльністю. Найкраще суть гри визначив Й. Хейзинга: “Ми можемо назвати гру, - пише він у роботі “Homo ludens” – вільно діяльністю, яка усвідомлюється як “несправжнє” і поза повсякденним життям виконуване заняття, однак вона може цілком захопити гравця, не переслідуючи при цьому ніякого прямого матеріального інтересу, не шукаючи користі, - вільною діяльністю, яка відбувається усередині навмисно обмеженого простору та часу, протікає упорядковано, за визначеними правилами та громадських угрупувань, що визначають за краще оточувати себе таємницею або підкреслюють свою відмінність від іншого світу всіляким маскуванням. У цьому визначенні є усі вичерпні пояснення того, чому гра настільки приваблива для будь-якої людини будь-якого віку і звідки багатство її навчальних, розливальних, вдосконалюючи особистість можливостей”.
Покажемо на невеликому прикладі, узятому зі сфери педагогіки, принципову відмінність гри як діяльності від гри іншого типу, скажімо, гри як засобу. Педагоги активно використовують гру як прийом, що дозволяє їм вирішувати педагогічні, насамперед навчальні, завдання: для підвищення інтересу дітей до ходу уроку та їхньої активності, для переключення уваги або відпочинку застосовуються різні активні методи, до яких відносяться й ігрові прийоми. Але при цьому кожен педагог добре розуміє, що гра для нього – це тільки засіб вирішення навчального завдання, яскрава “обгортка” навчального матеріалу, тому він ретельно відбирає ігри, які не виведуть дітей з-під його контролю, не захоплять їх настільки, щоб вони психологічно переключилися з уроку на ігрову взаємодію. Зрозуміло, що справжній педагог віддасть перевагу добре відомим ігровим формам і побудує урок із застосуванням ігрових елементів. Таких уроків у арсеналі сучасного вчителя багато, що можна тільки вітати.
Однак існує й інша можливість застосування гри в навчальному процесі, наприклад, під час проведення виховної години для вирішення різних проблем класного колективу. У цьому випадку доречним будуть ігри, які сприяють:
- зміцненню колективу;
- розвитку соціально-комунікативних навичок;
- адаптації учнів у колективі;
- коригування девіантної поведінки;
- розвитку толерантності тощо.
У такому разі весь простір уроку займає ігровий сюжет з його ігровими правилами й ігровою логікою розвитку. А всі знання, вміння та навички, які вчитель хотів би передати учням на цьому уроці, виступають як ігрові засоби. Це важливо в будь-якому віці, а в дитячому та підлітковому – особливо. Всі описані вище фактори створюють навколо психологічних ігор ореол привабливості, але поряд з цим – серйозну професійну проблему, бо вчитель повинен достатньою мірою володіти як психологічними знаннями, так і вмінням проведення ігор.
Для певної категорії дітей (та деяких дорослих) бажання грати приховує потребу в сильному та цілісному емоційному переживанні, яке особливо характерне для молодших школярів. Зазвичай для цього віку такий стан речей і є нормальним: ігри надають їм можливість емоційно реагувати на різні хвилювання і труднощі створення на рівні почуттів стосунків з оточуючими, навчитися контролювати і регулювати свій внутрішній світ. Однак іноді в деяких дітей таке ставлення до гри зберігається надовго - і не лише в дитинстві.
Для іншої групи людей (в основному для школярів 11-14 років) гра є безпечним простором побудови стосунків з оточуючими. Хлопчики – дівчатка, послідовники – лідери, знедолені – “зірки”, усі ці системи відносин підліткам досить важко усвідомлювати, будувати та змінювати в реальному житті, а от гра надає їм таку можливість. Пристрасть до колективних ігор величезна: у цьому віці діти настільки ж охоче грають, наскільки неохоче обговорюють наслідки гри на чуттєвому рівні.
Гра виступає як лабораторія, засіб пізнання та розвитку. У групі ці три варіанти сприймання гри виступають і як індивідуальні особливості окремих учнів, і як етапи особистісного розвитку.
У систематичну роботу з розвитку “ігрового потенціалу” школярів закладено великий зміст. Під час такої роботи гру можна розглядати як один з найважливіших напрямів не тільки діяльності шкільного психолога, але й роботи класного керівника. Без навчальної підтримки дорослих саме собою розвинення учнів не відбувається. Прив’язування різних типів відносин до певних вікових категорій має штучний характер, або можна сказати, що воно є адекватним тільки тоді, коли діти з перших днів навчання в школі залученні до систематичного ігрового процесу. З іншого боку, вік дитини дещо обмежує можливості розвитку: почніть, наприклад, цілеспрямовано залучати до гри семирічних, і вони за короткий проміжок часу пройдуть і перший, і другий етапи “ігрового розвитку”, а ось шестирічним малятам осмислення цих відносин у грі дається з величезними труднощами.
Учень включається в гру цілком: усім інтелектуальним, особистісним, емоційним потенціалом, життєвим досвідом і творчими ресурсами. Гра обумовлює певні правила поведінки учасників, межі дозволеного, тимчасові обмеження конкретного ігрового простору. Гра є “експериментальним майданчиком” особистості, дозволяє почувати себе вільним від будь-яких обмежень (стереотипів, шаблонів мислення і звичайних варіантів розв’язання проблеми).
Гра як психологічний метод у школі може бути використана як мінімум для вирішення трьох послідовних завдань:
- навчити дітей жити в ігровому просторі, цілком занурюватися в ігровий світ та ігрові відносини;
- навчити бути вільними в ігровому просторі, усвідомлювати власні цінності та налагоджувати стосунки зі сторонніми;
- навчити осмислювати ігровий досвід, використовувати гру як інструмент самопізнання та життєвих експериментів.
- Спільна діяльність викладача й учня, коли їхні цілі збігаються, має результатом плідне засвоєння матеріалу.
Ігри повинні відповідати наступним психолого-педагогічним умовам:
1/ сприяти зміцненню колективу;
2/мати пізнавальне значення;
3/ активізувати громадську позицію учнів;
4/ забезпечувати участь у грі переважної більшості учнів;
5/ створювати умови для індивідуальної та групової творчості).
Багато залежить і від ігрової позиції ведучого, якому слід:
1/ реалізовувати наявний ігровий план (тому що до гри педагог повинен ставитися досить серйозно та на час гри зрікатися своєї звичайної авторитарної позиції);
2/ виявляти прихильне ставлення до учнів, бути відкритим, сприйнятливим і трохи інфантильним;
3/ сприяти формуванню переконаності в необхідності ігрової поведінки;
4/ швидко переходити від реального до ігрового плану через гумор або байки;
5/ демонструвати широкий діапазон ігрових прийомів).
Тільки в цьому випадку ігрова позиція педагога буде сприяти реалізації основних її функцій: гуманізації взаємин педагога з учнями, підвищенню творчого потенціалу колективної діяльності, економії нервових витрат учителів і учнів і, нарешті, забезпеченню гнучкої поведінки педагога.
Це важливо не тільки для розуміння індивідуальних особливостей розвитку дітей, але і для розкриття їхніх вікових особливостей. Л.І. Божович зазначає, що зрозуміти вплив середовища на формування вікових особливостей дитини можна тільки в тому випадку, якщо врахувати як зміни в середовищі (наприклад, при переході з дитячого садка до школи), так і зміни в самій дитині, які обумовлюють характер впливу середовища на подальшій психічний розвиток дитини.
Л.С. Виготський вважав, що зрозуміти роль середовища в розвитку дитини можна лише тоді, коли підходити до неї з відносною, а не з абсолютною міркою. Це означає, що той самий вплив середовища по-різному позначається на дітях різного віку залежно від вікових особливостей. Таким чином, на думку Л.С. Виготського, той самий вплив середовища може розрізнятися залежно від того, на які психологічні особливості дитини він накладається. Ці особливості (індивідуальні та вікові), являючи собою внутрішні фактори, виступають як реальні фактори розвитку. Співвідношення зовнішніх вимог середовища (зовнішні фактори) з можливостями і потребами самої дитини (внутрішні фактори) становить основну ланку, яка і визначає подальший розвиток дитини.
Внутрішні фактори розвитку, з погляду Л.І. Божович, є системою, яку вона позначає поняттям “внутрішня позиція дитини”. Внутрішня позиція характеризується відношенням дитини до того об’єктивного становища, яке вона хоче посідати. Ця позиція базується на досвіді дитини. Її можливостях, потребах і прагненнях і обумовлює структуру відношення дитини до дійсності, до оточуючих і до самої себе. З точки зору Л.І. Божович, через внутрішню позицію відбиваються впливи навколишнього середовища.
Важливо мати на увазі, що вплив, який середовище справляє на дитину, а також вимоги, що йдуть від цього середовища, тільки тоді стають факторами розвитку дитини, коли ці вимоги є складовою структури власних потреб хлопчика або дівчинки. Дитина прагне виконання вимог середовища, якщо її виконання не тільки забезпечує відповідне об’єктивне місце дитини серед оточуючих, але і дає можливості посісти те місце, якого вона сама прагне, тобто задовольняє її внутрішню позицію. Зміни, які відбуваються в дитині до кінця вікового періоду, позначаються як психологічні утворення та можуть бути зафіксовані як зміни в розвитку психічних процесів, особистості та самосвідомості.
Послідовники Л.С. Виготського, А.Н. Леонтьєв і Д.Б. Ельконін, додали до характеристики віку посилання на провідну діяльність, усередині якої здійснюється розвиток дитячої психіки.
У кожному віці виділяють свою провідну діяльність:
- у дитинстві – безпосереднє емоційне спілкування;
- у ранньому віці – предметну діяльність;
- у дошкільному віці – гру;
- у молодшому шкільному віці – навчання;
- у підлітковому віці – спілкування;
- у юнацькому віці – професійне навчання.
А.Н. Леонтьєв виділяє три ознаки провідної діяльності:
1/ усередині провідної діяльності виникають і диференціюються інші, нові види діяльності;
2/ у процесі провідної діяльності формуються або перебудовуються окремі психічні процеси;
3/ від провідної діяльності залежать основні особистісні новоутворення дитини.
Д.Б. Ельконін додає ще дві ознаки провідної діяльності, у яких викладено залежність провідної діяльності від зовнішнього світу (світу людського та предметного):
1/ провідною діяльністю найбільш повно представлені типові для цього періоду розвитку відносини дитини з дорослими;
2/ провідна діяльність пов’язує дитину з тими елементами навколишньої дійсності, які в цей період були джерелом її психічного розвитку.
Таким чином, провідна діяльність обумовлює головні зміни в розвитку психічних процесів особистісних особливостей дитини на конкретній віковій стадії.
Л.С. Виготський вважає, що від 7 років дитина здатна регулювати свою поведінку з допомогою мовлення. А психічні процеси від цього часу починають керуватися за допомогою інтелекту, тобто стають опосередкованими або довільними.
Найпоширеніший, найпростіший вид гри – це так звані “ігрові оболонки”. У цьому випадку гра використовується як деяке оздоблення, загальне тло психологічної роботи, яка за своєю сутністю може бути неігровою, а – найчастіше – тренінговою. Наприклад: діти потрапляють до якогось чарівного світу, де вони повинні пройти випробування, для того щоб щось знайти, когось врятувати або просто повернутися додому. Кожне випробування є завданням на розвиток певних навичок, встановлення відносин між дітьми або з педагогом тощо. Гра у цьому випадку виступає “міфом”, захисним шаром тренінгової роботи, який надає цій роботі привабливості та цікавості в очах учасників. “Ігрові оболонки” дуже часто використовують в початковій школі. Найбільш активно сьогодні психологи-освітяни використовують “ігрові оболонки”, побудовані за принципом: злі сили щось вкрали, сховали, зламали, добрі герої, не шкодуючи сил, відновлюють справедливість, рятують і захищають слабких.
Для першокласника дії дорослого, спрямовані на його виховання й навчання, цілком зрозумілі. Але коли вчитель починає на уроці гратися, більшість дітей ставляться до цього насторожено: “Чи справді з нами граються, чи тільки прикидаються?”
Тому вчитель повинен вміти гратися по-справжньому, вміти піднятися до рівня дитини, зрозуміти й прийняти її позицію. І це важливе вміння дорослої людини стати на один рівень з дитиною щедро винагороджується – живою активністю сприйняття, щирою любов’ю до вчителя. Пізніше легше непомітно перейти від чистої гри до навчальної діяльності, зберігши, між тим, її ігровий характер (прийняття “рівного” партнера, збереження подвійного плану дії, вільного вибору дій партнерами тощо).
На мою думку основною проблемою в першому класі залишається парадоксальний факт: діти, приходячи з дитячого садка, не вміють гратися. Незважаючи на досить глибоку діагностику під час вступу до школи, ніхто всерйоз не ставить запитання: “А чи вміє дитина гратися?” Проте сформованість ігрової діяльності виявляється основою і для формування спочатку навчальної, а згодом і трудової діяльності.
Потрапляючи до школи після дитячого садка, дитина зустрічається з новим для неї видом діяльності – навчанням. Але гра залишається важливим засобом не тільки відпочинку, а й творчого пізнання життя, потужним мотивом навчання. Ігрова позиція – могутній засіб виховного впливу на дітей. Відомо, що ті діти, з яких на уроці й “слова не витягнеш”, в іграх активні. Вони можуть повернути хід гри так, що деякі відмінники тільки руками розведуть руками. У процесі гри в учнів виробляється звичка зосереджуватися, самостійно міркувати. Захопившись грою, діти зважають, що вчаться, до активної діяльності залучаються навіть найпасивніші.
Залежно від віку дитини, ігрова мотивація повинна змінюватись. Так, у першому класі я використовую іграшки, які стають персонажами уроків.
Іграшки можуть бути різними, але краще, якщо це будуть “дитинчата”, а не “дорослі” звірі. Вони мають бути досить великими, симпатичними, найкраще – надягатися на руку.
Гра тільки здається легкою. Насправді вона вимагає від дитини максимуму енергії, розуму, витримки, самостійності. Використовую ігри на уроці, аби утримувати нестійку увагу дітей, давати нові знання, заохочувати учнів мислити.
Для створення навчальної мотивації я використовую різні ігри: дидактичні, рольові, вікторини, кросворди. Дидактична гра – це практична групова вправа з пошуку оптимальних рішень, застосування методів і прийомів у штучно створених умовах, які відтворюють реальні обставини. Під час гри в учня виникає мотив, суть якого полягає в тому, щоб успішно виконати взяту на себе роль.
На уроках закріплення вивченого матеріалу або його повторення намагаюся щоб діти працювали в парах. Попередньо готую картки з 2-3 практичними завданнями з теми, що вивчається. Одержавши картку, двоє учнів перше завдання виконують разом. Один пояснює, як потрібно виконувати завдання, а інший слухає, запитує або висловлює свою думку. Друге й третє завдання діти виконують кожен окремо, записуючи їх у зошитах, а потім перевіряють один в одного з коментуванням помилок, яких припустилися.
Слід зазначити, що гра – це, як правило, переживання, тому найбільш активізується під час гри емоційна сфера.
Наприклад, на уроці навчання грамоти не просто вивчаємо якусь букву, а запрошуємо дітей на день народження цієї букви. Кожній групі даю особливе завдання:
- запросити гостей – казкових персонажів, до складу імен яких входить буква й звук, що вона позначає;
- принести подарунки: квіти, книги, у назвах яких є цей звук;
- приготувати святкові гостинці з цим звуком;
- запросити дітей, в іменах яких є цей звук;
- назвати звірів, птахів, комах, у назвах яких є цей звук тощо.
Таким чином, діти в цікавій формі знайомляться з новою буквою й звуком (звуками), що вона позначає.
З досвіду своєї роботи я впевнилась, щоб ігрова діяльність на уроці була ефективною й давала бажані результати, необхідно нею керувати, забезпечивши виконання таких вимог:
- готовність учнів до участі в грі (кожний учень повинен засвоїти правила гри, чітко усвідомити її мету, кінцевий результат, послідовність дій, мати необхідний запас знань);
- забезпечення кожного учня необхідним дидактичним матеріалом;
- зрозуміла для учнів постановка завдань гри;
- поетапне проведення складної гри, поки учні не засвоять окремих дій, а далі можна пропонувати всю гру й різні її варіанти;
- контроль учителя має перетворитися на допомогу; влесне контроль варто передати самим учням;
- обов’язково має підтримуватись і стверджуватись гідності кожної дитини;
- групи утворюються з урахуванням рівня знань і розумового розвитку учнів;
- чітка організація гри і спрямування її на мету.
Надзвичайно важливу роль в ігровій ситуації відіграють правила. Якщо вони заздалегідь не продумані, чітко не сформульовані, то це утруднює пояснення ходу гри, осмислення учнями її змісту й може викликати втому і байдужість дітей.
Пропрацювавши в школі 20 років, досить часто переді мною постає проблема: невміння першокласників спільно працювати разом. Спостерігаючи за дітьми, я помітила, що вони працюють тільки з вчителем. Навіть коли вони звертаються один до одного, то погляд спрямований не на однокласника, а на мене. На початку вересня я провела з першокласниками гру, під час якої, діти що сидять у парах, виконують спільний малюнок “Справи, які можна робити разом”. Крім того, що під час виконання роботи діти вчилися працювати разом, я мала можливість побачити, хто вже готовий до подібного спілкування, а хто ні. Це своєрідний тест, що допоміг мені в роботі з першокласниками. Для формування вміння діяти спільно корисні ігри, у яких діти діють у командах, але не змагаються.
1.2. Сюжетно-рольові ігри, дидактичні розвивальні ігри
У багатьох психологічних іграх, що описані в сучасній літературі, діти теж кудись потрапляють, когось рятують. “Ігрові оболонки” можуть бути найрізноманітнішими: приміром, подорож на протязі від станції до станцій, рух усередині від рівня до рівня, створення візерунків у чарівному калейдоскопі тощо. Усе це – реальні сюжети, покладені в основу вже апробованих ігор.
У першому півріччі навчального року психолог і вчитель інтенсивно формують у дітей ігрові вміння та головним чином рольову поведінку. Вони залучають дітлахів до спільної гри або пропонують сюжет у вигляді невеличкої розповіді.
Перед педагогом стоїть завдання – стимулювати творчу активність дітей у грі. Цьому сприяє розгортання гри із включенням до неї різних ролей: з різних сфер соціального життя, з різних літературних творів, казок, а також поєднання казкових і реальних персонажів.
Включення в загальний сюжет таких ролей розвиває уяву дітей, їхню фантазію, спонукає придумати нові несподівані повороти подій, що поєднують і роблять осмисленим співіснування та взаємодію таких різних персонажів. При цьому вчитель враховує інтереси тих дітей, які у звичайних спільних іграх часто не можуть реалізуватися. Педагог у спільній з дітьми грі повинен продемонструвати, як можна розгорнути сюжет з такими, здавалося б, непоєднуваними ролями: усіляко заохочує дітей, які вводять у попередній план гри нові ситуації, події та дійових осіб. Тому що це є показником вільного володіння ігровими засобами діяльності та творчої активності дитини.
Створення умов для сюжетно-рольової гри або моделювання відсутніх предметів під час сюжету, який вже розгорнувся, допомагає чіткіше позначити ігрову ситуацію, цікавіше здійснити ігрові дії, точніше узгодити задум гри між її учасниками. Звичайно, для цієї мети використовується готовий матеріал, іграшки. При цьому важливо пам’ятати, що обставини, умови та оточення повинні бути не тільки зручними для гри, але і схожими на справжні, тому що не всі діти відразу можуть сприймати чисто символічну, удавану ситуацію (особливо це стосується групових ігор, де для всіх учасників важливо позначити ситуацію гри в предмети).
З допомогою дидактичних ігор діти вчаться порівнювати та групувати предмети як за зовнішніми ознаками, так і їхнім призначенням; вирішувати завдання.
Такі ігри рекомендовано включати як додаткові розвивальні вправи під час уроку: фізкультхвилинки, хвилинки релаксації тощо. Подібні ігри сприяють розвитку психічних процесів дитини, розвивають зосередженість, увагу, наполегливість, пізнавальні здібності, пам’ять та інтелект. У свою чергу, добре розвинені психічні процеси сприятимуть розвитку пізнавальної зацікавленості й мобілізації навчання.
Особливе місце займають ігри, які створюють самі діти, - їх називають творчими або сюжетно-рольовими. У цих іграх молодші школярі відтворюють у ролях усе те, що вони бачать навколо себе в житті та діяльності дорослих. Творча гра найбільш повно формує особистість дитини, тому є вагомим засобом виховання. Творча гра як важливий засіб всебічного розвитку дітей пов’язана з усіма видами їхньої діяльності, цим визначається її місце в педагогічному процесі школи. Для кожного класу – першого, другого чи четвертого – визначено завдання виховання та розвитку, які вирішуються з допомогою гри. Цікаві ігри створюють бадьорий, радісний настрій, роблять життя дітей повним, задовольняють їхню потребу в активній діяльності. У грі дитина починає відчувати себе членом колективу, справедливо оцінювати дії та вчинки своїх товаришів і свої власні. Завдання психологів і вчителя полягає в тому, щоб зосередити увагу гравців на таких цілях, які викликали б спільність почуттів і дітей, сприяти встановленню між дітьми відносин, заснованих на дружбі, справедливості, взаємній відповідальності. Втілення життєвих вражень у грі – складний процес, творчу гру не можна підкоряти вузьким дидактичним цілям, з її допомогою вирішуються першочергові виховні завдання. Найважливіша умова успішного керівництва іграми – вміння здобути довіру дітей, встановити з ними контакт, що досягається лише за умови серйозного та щирого інтересу педагога до гри, розуміння їхніх задумів, переживань: у грі розкриваються особливості кожної дитини, її інтереси, різні риси характеру. Спостереження за дітьми в процесі цього виду діяльності дають педагогові та психологові багатий матеріал для вивчення учнів, допомагають знайти правильний підхід до кожної дитини.
Основний шлях виховання в грі – вплив на її зміст, тобто на вибір теми, розвиток сюжету, розподіл ролей і на реалізацію ігрових постатей: розігруються ролі тварин, героїв з казок; створюючи ігровий образ, дитина не тільки всебічно виражає своє ставлення до обраного героя, але і виявляє особистості якості. У молодшому шкільному віці більший ігровий досвід, більш розвинена уява допомагають дітям самим вигадувати цікаві сюжети, якщо вдається “затягнути” дітей сюжетом, гра виникає природно навіть без пропозиції керівника. Однак педагог може і порадити дітям тему гри, якщо впевнений, що вона зацікавить їх. Організація ігрового простору для особистості кожної дитини в групі, в колективі – одне з найважливіших і найскладніших питань педагогіки молодшого шкільного віку. Якщо ж гра сильно захоплює дитину, якщо дитина усвідомлено і глибоко увійшла в роль, ігрові переживання перемагають егоїстичні поривання. Завдання педагога – виховувати дітей на кращих прикладах з життя і діяльності людей, що сприяє формуванню позитивних почуттів і вражень.
Під час організації гри перед психологом і педагогом постають складні питання: кожній дитині хочеться бути головним, але не всі вміють заважати на думку товаришів, справедливо розв’язувати суперечки, тому обрання організатора в класі потребує особливої уваги (не кожному під силу впоратися з цією роллю, але у всіх без винятку дітей необхідно виховувати активність і організаторські вміння).
Особливого значення в навчально-виховному процесі слід надавати дидактичним іграм. В умовах дидактичної гри дитина засвоює програму значно успішніше, ніж в умовах навчального заняття, адже в дидактичній грі навчальна мета – частина ігрової ситуації з виконанням певних правил. За таких умов засвоєння нового матеріалу відбувається без особливого напруження, ніби саме собою. Гра сприяє розвитку психічних процесів, нових видів розумової діяльності, засвоєння молодшими школярами нових знань та вмінь. Поетапне відпрацювання розумових дій в дидактичній грі відбувається довільно і ненав’язливо.
Важлива роль гри в розвитку психічних процесів дитини пояснюється тим, що гра озброює дитину доступними для неї засобами активного відтворення, моделювання з допомогою зовнішніх, предметних дій. У грі дитина швидше і легше дотримується свідомої мети запам’ятати і запам’ятовує більший обсяг матеріалу, ніж під час звичайного уроку. Саме в грі розвивається здатність дитини створювати узагальнені типові образи, подумки перетворювати їх.
Перед організацією гри я обмірковую і планую діяльність конкретних учнів з урахуванням їх психологічних особливостей, ролі лідерів і малоактивних дітей. Адже гра є гарним засобом розвитку вольової сфери дитини. Саме в грі проявляється бажання добровільно, з власної ініціативи виконувати різноманітні правила, дотримуватися вимог, саме гра дає дітям можливість спробувати себе у ролях і “керівника, і “підлеглого”. Цінність ігрової діяльності виявляється і в тому, що в ході гри діти мають можливість активно спілкуватися, а це сприяє формуванню дитячого колективу.
Специфічному структурними елементами гри є дидактична мета, ігровий задум, правила гри, ігровий початок, ігрові дії, підбиття підсумків.
Дидактична мета ігор різноманітна:
- розвиток умінь порівнювати, визначати головне;
- розвиток уяви, спостережливості;
- розвиток фонематичного слуху, закріплення правильної артикуляції;
- розвиток вміння співвідносити елементи різних множин, встановлювати відповідності, співвідносити числа і цифри;
- формування умінь визначати ознаки явищ і предметів, диференціювати їх суттєві і несуттєві, встановлювати причиново-наслідкові зв’язки тощо.
Ігровий задум має постати перед шестирічними школярами у вигляді уявних перешкод, активної дії з предметами, чогось загадкового, таємничого, перевірки своїх можливостей в змаганні, рольового перевтілення, загальної рухової активності тощо.
На створення ігрової атмосфери суттєво впливає ігровий початок. Атмосферу гри забезпечую під час поділу на команди, вибору ведучого або командира (капітана), визначення права першого ходу за допомогою лічилок, ігрових розрахунків чи жеребкувань.
Власне, ігрові дії для дітей найбільш цікаві: вийти за двері, а потім відгадати, що змінилося; впізнати із зв’язаними очима товариша або предмет із “чарівної торбинки”; найшвидше і правильно розкласти предмети; скласти (придумати) слова тощо.
Ігрові дії пов’язані з ігровим задумом, випливають з нього, є засобом реалізації ігрового задуму. Тому в процесі гри домагаюсь виконання учнями дій, спрямованих на досягнення поставленої дидактичної мети. Наприклад, вивчаючи тему “Взаємне розміщення предметів у просторі”, маленькі учні діють відповідно до уявної ситуації: переміщують предмети, накладають їх один на одного, пояснюють свої дії однокласникам. Змінюючи місцезнаходження предмета, діти усвідомлюють просторові співвідношення, а пояснюючи, закріплюють відповідну термінологію. Виконуючи ігрові дії, зацікавившись ними, діти легко справляються із прихованим у грі навчальним змістом.
Відповідно до задуму ігрової дії підбираю різні: відгадування загадок (“Чарівна торбинка”); рольові дії відповідно до ігрових ситуацій (“Перукарня”, “Магазин”, “Лікарня”); малювання за уявою або інструкцією; рухи на увагу (“Будь уважним, заборонений рух”); дії, засновані на класифікації або порівнянні предметів (“Добери за формою”); складання заданих фігур (“Тангарм”); просторові перетворення.
Підбиваю підсумки гри одразу після її закінчення: підраховую бали і визначаю переможців, а також тих дітей, хто найбільш правильно виконав ігрове завдання. У ході гри та після її закінчення обов’язково відзначаю досягнення кожної дитини, підкреслюю її успіх, виявляю оптимістичне ставлення до можливостей дітей та делікатність у висловлюванні оцінних суджень.
Під час проведення дидактичних ігор підтримую дух змагання, емоційне забарвлення гри, об’єктивно і позитивно оцінюю успіхи дітей з точки зору не лише розв’язання дидактичного завдання, а й участі в ігрових діях: хто грав чесно, не підглядав, придумав цікавий хід угрі, допомагав друзям. Поглядом, інтонацією, мімікою, жестами намагаюся викликати позитивні емоції, створити бадьорий настрій.
Підбиваючи підсумки співпраці з дітьми за день чи за тиждень, обов’язково слід надати можливість учням оцінити спільну діяльність.
Готуючись до уроку, я прагну правильно забезпечити ігровий план діяльності дітей, щоб інтереси одних не задовольнялись за рахунок інших, щоб школярі поступово привчались до норм поведінки під час гри, вчилися гальмувати небажані прояви. Зважено обмірковую розподіл ролей під час гри, враховуючи індивідуальні психологічні особливості дітей.
Добираючи гру до конкретного уроку, продумую відповідність мети дидактичної гри навчальній меті уроку, враховую посильність завдань, продумую методи і форми організації навчальної діяльності учнів, які б сприяли максимальній активізації їх емоційної сфери і розумової діяльності. Саме парні і групові форми виконання формують у дітей позитивну мотивацію до навчальної співпраці.
Іграм, що містять важкі завдання, мають передувати простіші, більш легкі. Вони готують дітей до подолання навчальних труднощів, забезпечують успіх у складних іграх.
Молодших школярів слід привчати до зосередженої самостійної роботи, формувати вміння визначати посильний обсяг роботи, працювати на уроці з повною вдачею, не втрачаючи жодної секунди дорогоцінного часу, щоб після його закінчення відчути задоволення від гарно виконаної роботи.
1.3. Розвиток у грі творчих здібностей учнів
Психологічні та педагогічні дослідження свідчать про те, що початок розвитку творчих здібностей дітей припадає на дошкільний вік, коли змінюється характер їхньої діяльності порівняно з раннім дитинством. Цей тип діяльності Л.С. Виготський характеризує як перехід до творчої діяльності, “якщо мати на увазі той факт, що у всіх видах діяльності дошкільника виникає зовсім своєрідне співвідношення думки та дії, саме можливість втілення задуму. Можливість йти від думки до ситуації, а не від ситуації до думки. Чи візьмете ви ігри, малюнки, працю, - скрізь і в усьому ви будете мати справу із абсолютно новими співвідношеннями, які виникають між мисленням і діями дитини”. Уява старших дошкільників і молодших школярів набуває усе більш активного характеру, в них розвивається здатність до творчої діяльності. “Це підтверджується і тим, що більшу увагу діти починають приділяти ідеї, тобто задуму свого витвору. Звичайно, ані дошкільник, ані навіть школяр не намагається передати якусь абстраговану думку в образній формі. Ідейний задум 6-7 річної дитини зазвичай вичерпується сюжетом її малюнка, гри або розповіді”, - стверджує Л.С.Виготський.
Глибокий і складний процес перетворення і засвоєння життєвих вражень відбувається саме в іграх, творчий початок проявляється також у задумі – обранні теми гри, малюнка, засобів здійснення задуму та в тому, що діти не копіюють побаченого, а з великою щирістю та безпосередністю, не приймаючись справленим враженням, передають своє ставлення до зображуваного, свої думки та почуття. На відміну від дорослих діти не здатні у подробицях обміркувати майбутню роботу або гру, вони намічають лише загальний план, який і реалізують у процесі діяльності. Завдання психолога та педагога – розвивати творчі здібності дитини, ціле спрямувати уяву, спонукати її в будь-якій справі переходити від думки до дії. Дитяча творчість заснована на наслідуванні, яке служить важливим фактором розвитку дитини, зокрема її художніх здібностей. Завдання педагога – спираючись на схильність дітей до наслідування, прищеплювати їм навички та вміння, без яких неможлива творча діяльність, виховувати в них самостійність, активність у застосуванні цих знань та вмінь, формувати критичне мислення, цілеспрямованість. Творча уява дитини особливо яскраво виявляється і розвивається у грі, деталізуючись у цілеспрямованому ігровому задумі: у грі часто проявляються емоції, які у житті їм ще невластиві. Ігрова творчість виявляється також у пошуках засобів для зображення задуманого: діти реалізують свій задум з допомогою мови, жестів, міміки, застосовуючи різні предмети, конструкції, будови. У грі з особливою силою виявляються індивідуальні особливості дітей, які також впливають на розвиток творчого зауму.
На жаль, маємо відзначити нестачу увагу до розливальних функцій навчання в школі: орієнтація на формування більш емпіричного, репродуктивного мислення призводить до того, що багато хто із завтрашніх фахівців, які добре знають шкільну програму, не в змозі використовувати ці знання в нестандартній обстановці, не володіють творчим мисленням, а спираються в основному на свою пам’ять, вагаються, відповідаючи на проблемні питання навіть тоді, коли мають під рукою підручники та навчальні посібники.
Сьогодні питання про розвиток творчих здібностей учнів у теорії та практиці навчання постало особливо гостро, тому що останні дослідження виявили в школярів значно більші, ніж вбачалося раніше, можливості засвоювати наукові поняття, знання та вміння як у звичних, так і в нестандартних ситуаціях. Такий стан речей викликав необхідність розробки нових дидактичних підходів до навчання школярів, які враховують не тільки накопичення знань, але й цілеспрямоване засвоєння – в умовах застосування евристично орієнтовних методів навчання – систем, понять, закономірностей, узагальнених структур, які дозволяють глибше усвідомити сутність конкретного навчального предмета і на цій основі опанувати загальні прийоми вирішення найрізноманітніших завдань.
Процес навчання може протікати з різним докладанням сил, пізнавальної активності та самостійності школярів: в одних випадках він має наслідувальний, репродуктивний характер, в інших – пошуковий, а іноді й творчий. Саме характер навчального процесу впливає на його кінцевий результат – рівень набутих знань, умінь і навичок.
У теорії та практиці навчання питанням розвитку творчих здібностей учнів поки що не приділяється достатньої уваги, не сформульовано цілий комплекс показників, що складають поняття “творчі здібності”, уповільнено розробляються діагностичні методики оцінювання їх рівня – все це гальмує широке впровадження ідей розвивального навчання в практику освітньої школи. Зрозуміло, побачити щось по-новому, не так, як усі, і не так, як ти бачив раніше, - завдання не з легких, проте цьому можна навчити, якщо спрямувати процес навчання на розвиток і вдосконалення творчих здібностей учнів.
Як правило, у традиційному навчанні власне творчі завдання є засобами діагностики вже сформованих творчих здібностей учнів. Нас же повинна цікавити проблема цілеспрямованого, керованого з боку вчителя розвитку цих здібностей з допомогою спеціальної системи пізнавальних завдань, під час вирішення яких у школярів природним чином з’являється інтерес не тільки до знань, але й до засобів їх здобуття. Учні стикаються також і з естетичною стороною розумової праці, коли вони вчаться порівнювати кілька засобів вирішення одного завдання як за правильністю, раціональністю, так і за “красою” – простотою, добірністю, локанізмом.
Слід окремо відзначити, що не варто готувати творчі завдання персонально для найбільш здібних учнів і пропонувати їх замість звичайних завдань, які пропонуються всьому класу: такий спосіб індивідуалізації не можна вважати кращим, тому що він ставить у свідомо нерівні умови дітей, поділяє їх на здібних і нездібних, - таким чином, завдання творчого характеру треба готувати для всього класу. Під час виконання таких творчих завдань оцінювання є не наслідком тільки успішного виконання: вчитель повинен завжди уважно вислуховувати учня, бачити в кожному школяреві індивіда з особливими можливостями та обдаруваннями. Так, відомий американський психолог Розенталь стверджував, що в ситуації, коли педагог очікує видатних успіхів від дітей, необхідним є розумне керівництво з боку дорослих. Завдання педагога: використовуючи різноманітні методи навчання, у тому числі й ігрові, цілеспрямовано розвивати в дітей гнучкість мислення, наполегливість у досягненні мети, ділову активність; вчити дітей розмірковувати, різнобічно підходити до проблем, робити висновки, знаходити нові, оригінальні відповіді, одержувати несподівані, однак позитивні, результати, відчувати задоволення від процесу навчання.
Сучасні психологи згодні в тому, що більшість дітей та – як це не дивно – дорослих успішно вирішують проблеми та завдання, запропоновані в ігровій формі. Визнаючи неабияку роль гри в житті людини, схиляючи перед нею голову, А.Ейнштейн писав: “Теоретична фізика – це дитячі іграшки порівняно з грою”. Важливо пам’ятати, що гра впливає на навчальну діяльність, особливо інтелектуально пасивних дітей (виконуючи в процесі гри велику розумову роботу, такі діти активізують власну діяльність). Творчість є не більш як проекцією дитячих ігор на життя дорослих: якби ж то процеси, з якими вони пов’язані, - подив і цікавість, жагу експериментування, пошуки та знахідки – можна було б захистити від вікового нівелювання, якби ж то можна було досягти їхньої переваги в поведінці дорослого, то використовуючи творчий потенціал у своїй діяльності, можна було б подолати багато вершин. Немає секрету в тому, що з кожним роком зростають вимоги до розумової діяльності людей, тому останнім часом зростає і кількість тих, хто навчає, та тих, хто навчається, продовжуються терміни навчання, збільшується обсяг засвоюваних знань. Дотепер цей шлях приносив виразні результати, але стає очевидним, що такий процес має певні межі: неможливо безмежно збільшувати час навчання. Зусилля педагогіки з удосконалення системи навчання в останні роки концентрувалися переважно на поліпшенні змісту та підвищенні якості викладання, розроблялися нові методи навчання. Однак у той час, як процес передачі знань інтенсивно вдосконалювався, методам засвоєння та практичного застосування цих знань приділялося порівняно мало уваги. Внаслідок чого виникло протиріччя: вимоги до розумової діяльності учнів безупинно зростають, а їхня здатність засвоювати та використовувати набуті знання залишається на досить низькому рівні.
Нагадаємо, що необхідність виховання високообдарованих нащадків людство усвідомило досить давно: у Китаї, за часів Конфуція, особливо обдаровані діти здобували освіту при дворі правителя, в них вбачили гарантів майбутнього національного процвітання і високо шанували їх.
У наші дні також існують спеціальні програми роботи з талановитими дітьми. А от діти з нестандартними здібностями опинялися та й опиняються в найнесприятливішому становищі, від них не вимагають більше посередніх оцінок.
Величезне значення для РТЗ (розвитку творчих здібностей) мають рівні розвитку таких психічних процесів, як різновиди пам’яті, мислення, уваги, уяви. Такий розвиток здійснюється з допомогою спеціальних ігор і вправ: це тривала, цілеспрямована робота, тому епізодичне використання ігор не принесе бажаного результату; інтелектуальні завдання повинні поступово формувати і розвивати всі рівні інтелектуальної та творчої діяльності учнів, ефективно використовуватися на практиці.
Прийшовши до школи, малюки повинні переключитися на навчання. Не всім це вдається однаково легко. І, щоб полегшити перехід від ігрової діяльності до навчальної, я використовую на уроках ігрові прийоми, вводжу в навчальний процес ситуації з ігровою мотивацією, тому що в умовах гри шестирічки зосереджуються краще і запам’ятовують більше, ніж в умовах, коли їм пропонують просто запам’ятати. Я граю з учнями не заради гри, а для того, щоб у всіх пробудити вогник цікавості та допитливості.
Частими гостями у нас на уроках були Гномик, Клоун, Дюймовочка. Вони знайомили дітей з новою буквою, пропонували цікаві завдання. Цікаво проходять у нас ігри “Подорож у ліс”, “Космічна подорож”. На шляху ми робимо зупинки, на яких дітей чекають герої улюблених казок. Вони дають завдання, які малюкам потрібно виконати. Беручи участь в іграх, діти виявляють велику активність, адже всі бажають бути покупцями, пасажирами, водіями. Гра – це школа соціальних відношень. В умовах ігрових співвідношень дитина добровільно тренується. У грі це відбувається значно легше, ніж у житті.
Читаючи казки й оповідання, розігруємо діалоги. Спостереження показали, що пам’ять дітей шестирічного віку дозволяє відтворити дослівно цілі текстові уривки.
Школа – це не тільки навчання, а й світ спілкування, радощів, переживань, світ краси, гри, казки, музики, малюнка, світ фантазії, творчості.
Ось чому на уроках я використовую різні ігрові методи й прийоми, залучаю дітей до різноманітної діяльності, щоб дитина могла сама здобувати знання, спостерігаючи, робити висновки.
Я прагну, щоб між мною і моїми учнями панувала атмосфера поваги і взаємоповаги, довіри і співчуття.
У роботі з шести річками дуже важливим є вибір методів навчання. Але урок повинен мати оптимальне навчально-виховне навантаження, забезпечуючи результативність як вчительської роботи, так і навчальної діяльності учнів. Водночас треба запобігти їхньому перевантаженню, раціонально використовувати кожну хвилину уроку.
Отже, використовуючи у своїй роботі різні методичні посібники, які висвітлюють надбання досвідчених вчителів, додаючи свою наполегливість, знання і любов до дітей, турботу про їхнє майбутнє, можна чекати гарних результатів від наших маленьких доброзичливих школярів, яких нам довіряють батьки і держава.
ВИСНОВОК
На моє велике переконання ми, вчителі початкових класів, торуємо шлях дитини до подальшого пізнання. Ми завжди знаходимося поруч з дітьми в найважчі для них роки. Процес адаптації пройде, і ми помічаємо, що вони стали організованішими, уважнішими, легше включаються до роботи. Перед нами постають інші навчальні проблеми, більш серйозні і глибші.
Попереду – випробування, зусилля, нові аспекти в роботі.
Що дав мені досвід використання ігор?
Поєднання ігрових дій і серйозних завдань допомогло дітям швидше опанувати роль учнів. Гра завжди створювала бадьорий творчий настрій, і ні в якій іншій діяльності дитина не проявляла стільки наполегливості, цілеспрямованості, кмітливості, як в ігровій. Вона зробила цікавим процес навчання, сприяла полегшенню усвідомлення матеріалу. А я через ігрові форми вирішувала важливі виховні завдання – уміння турбуватись про оточуючих, толерантність, здатність співчувати й товаришувати. Гра, як і творчість, єднала дітей і вчителя, вчила оптимізму, життєлюбству, взаєморозуміння. Вона сприймалася як радісний підсумок здійснення планів, реалізація перспективи. Одночасно з грою непомітно для дітей відбувався їхній саморозвиток, саморозвиток, самовиховання. Я переконалася, що гра розкриває дітей краще від діагностичних тестів. Це для вчителя в майбутньому - великий простір для спостережень і роздумів. Орієнтація на гру як спосіб навчання й форми організації діяльності допомогли мені зробити працю приємною, стосунки з учнями – приязними та довірливими, а навчання - цікавим та захоплюючим.
На уроках не буває місця авторитарній формі спілкування, а панує спільна, колегіальна діяльність, співпраця, співтворчість.
Гра дарує учням радісні хвилини. А там, де учні бажають учитися, прагнуть навчатися, є позитивні емоції, є і результат.
Наше основне завдання – навчити дітей самостійно здобувати знання, тобто навчитися вчитися. І тут без теоретичних знань не обійтися. А коли засвоєння матеріалу йде в грі, дітям набагато легше й цікавіше працювати. «Навчаючись граючись», «Гру покличу на урок!» – не пусті гасла, а життєва необхідність творчо працюючого вчителя, який любить дітей і свою роботу. Для шестирічки гра ще залишається основним видом діяльності. А хіба ми, дорослі, граємо з меншим азартом чи запалом? Треба тільки пам’ятати, що все добре в межах розумного! Тож граймося!
Л І Т Е Р А Т У Р А
- Бурменская Г.В., Слуцкий В. Одаренные дети. – М.: Пргресс, 1991.
- Вакарчук Н.О. Ігрова взаємодія як засіб творчої самореалізації вчителя // Творча особистість учителя: проблеми теорії і практики. К.: НПУ, 1999.
- Гиппенрейтер Ю.Б. Общаться с ребенком. Как? – М.: «ЧеРо» при участии Творч. Центра «Сфера», 2001.
- Глассер Уильям. Школа без неудачников. – М.: Прогресс, 1991.
- Давыдов В.В. Сборник статей о развивающем обучении. – Томск: Пеленг, 1995.
- Зак А. Развитие логического мышления детей 5-16 лет. – Ярославль: Академия развития, 2000.
- Падалка О.С. та інші. Педагогічні технології – К.: Упр. енциклопедія. 1995.
- Пєхота, А.З. Кіктенко, О.М. Любарська та ін; Освітні технології: Нав. – метод. посіб. О.М. За заг. ред О.М. Пєхоти – К.: А.С.К. 2001
- Петрусинский В.В. Педагогические игры (выпуск 5).- М., 1994.
- Пометун О., Пироженко Л. Інтерактивні технології навчання: теорія, практика., досвід. – К. 2002
- Початкова школа № 42 2006. 11
- Початкова школа № 44 2006. 11
- Скворчевська О.В. Ігрові методики роботи з учнями 1-4 класів.
- Тихомирова Л.Ф. Развитие интеллектуальных способностей школьника. Популярное пособие для родителей и педагогов.- Ярославль: Академия развития, 1997.
- Толлингерова Д., Олоушева Д., Канторкова Г. Психология проектирования умственного развития детей. – Москва-Прага, 1994.
- Наволокова Н.П., Єнциклопедія педагогічних технологій – ТОВ «Видавнича гркпа «Основа», 2011 р.
- Початкова освіта, №21, 2007 рік.
- Початкова освіта, №22, 2007 рік.
ДОДАТКИ
Додаток 1
ПРИКЛАДИ ВИКОРИСТАННЯ МАТЕМАТИЧНИХ ДИКТАНТІВ НА УРОКАХ МАТЕМАТИКИ
Диктант 1. «Класичний»
Варіант А. Учитель диктує приклади (рівняння, задачів…), а учні записують лише відповіді. Така форма роботи дає змогу навчати дітей працювати в загальному ритмі, однаковому для всього класу.
Варіант Б. Хтось із учнів диктує завдання, а решта записують відповіді. Така форма роботи також учить працювати в загальному темпі (але темп більш уповільнений). Диктувати завдання доцільніше обирати учня, котрий має середній темп роботи.
Варіант В. На дошці записані завдання (на картці, у зошиті…), а діти фіксують лише відповіді. Така форма роботи допомагає продуктивно дібрати оптимальне індивідуальне навантаження для кожного учня. Довантажити тих, у кого темп роботи вище середнього, і дозволити працювати в уповільненому темпі учням з низьким темпом роботи.
Формує якість та швидкість обчислювальних навичок, увагу, зосередженість.
Диктант 2, «Математичний Марафон»
На дошці чи аркуші паперу пишемо приклади (завдання). Виграє той, хто швидше пройде дистанцію, правильно розв’язавши приклади (не зійшовши з дистанції).
Можна змагатися групами, парами, у парі, по рядах, варіантах тощо.
Стимулює швидкість лічби, дає можливість зацікавити дітей ігровою формою, урізноманітнює рутинну роботу на уроці.
Диктант 3, «Ти – мені, я – тобі» (робота в парі)
Учні по черзі задають оди одному приклади й контролюють запис відповіді. Помінявшись зошитами, оцінюють роботу.
Відповіді записують обидва учні, але «свої» відповіді кожен обводить кружечком чи підкреслює – так зручніше потім перевіряти.
Відповіді в обох зошитах мають бути однакові.
Вправа розвиває творчість, дає можливість попрацювати в одному ритмі, у «зв’язці», відчути лікоть друга, розраховувати на допомогу.
Тут може проявити себе навіть слабший учень, приклади вибираються за своїми можливостями. Сильний (ведучий)учень не дає схибити, заплутатись тощо. Можна оцінити роботу пари, підрахувавши кількість правильно розв’язаних прикладів. Щоб виграти змагання пар, ведучий і ведений докладають максимум зусиль, щоб підвести один одного.
Диктант 4. «Шумівки» (хоровий)
Учитель диктує диктант у будь-якій формі, а учні хором дають відповідь (шумлять0. Завдання дає змогу слабшому спертися на сильнішого. Якщо в хорі хтось «сфальшивив», то ті, хто поруч, ляскають у долоньки, і приклад пояснюється для тих, хто не зміг його розв’язат. Учитель одразу має змогу дізнатися, у кого проблеми з лічбою. Сильні учні отримують додаткове навантаження – виконують роль консультантів (помічників учителя.)
Диктант 5, «Естафета»
Кожен учень по черзі задає свій приклад (рівняння, задачу…), а решта його розв’язує і записує відповіді.
Варіант А. Учень-ведучий працює біля дошки, а решта – у зошитах.
Варіант Б. Перший учень у групі (ряду, варіант) розв’язує 1 приклад (на аркуші чи біля дошки), далі – другий, третій… Виграє той ряд (група, варіант ), який швидше й правильно розв’яже свої приклади.
Варінт В. перший учень розв’язує приклад, написаний для нього вчителем, і дописує свій – для наступного учня і т. д. Тут навантаження зростає, темп зменшується, але посилюється увага та зосередженість.
Диктант 6. «потяг»
У кожного на картці-вагончику 85-10-15 прикладів. Учитель (або сильніший учень) на картці-паровозику пише формулу, а діти на своїх картках- вагончиках записують і розв’язують приклади до формули.
Машиніст перевіряє картки-вагончики та чіпляє їх до потяга тільки тоді, коли вони правильно розв’язані . Поламані (з помилками) відсилає в депо на ремонт (виправляти помилки). Депо-група – сильні учні-консультанти пояснюють розв’язок приклада. Тоді вагончик-картку чіпляють до потяга.
Потягів може бути декілька (за темами, що вивчаються в цей ремонт). Відшукати свій потяг для картки-вагончика учень має самостійно.
Вправа дає учням можливості глибше засвоїти теоретичні знання, пов’язати теорію з практикою. Цінність гри в розподілі навантаження, диференціації та індивідуалізації роботи кожного учня. Упродовж диктанту йде одразу й індивідуальна, і парна, і групова, і колективна робота.
Працює кожен на своєму рівні, але просувається постійно вперед, на більш високий щабель драбинки пізнання.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
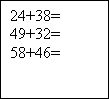
![]()

![]()
![]() Види формул:
Види формул:
![]()
![]()
![]()
![]()
![]()
Види Формул:
a + b=c,
a - b=c,
a • b=c,
a : b=c,
![]() P =(a - b) • 2;
P =(a - b) • 2;
![]() P =a • 4;
P =a • 4;
![]() P=a + b + c;
P=a + b + c;
![]() S=a • b;
S=a • b;
a + b + c=b + a + c…
Диктант 7. «Круговий»
Перший учень називає приклад, решта – записують і розв’язують його. Другий придумає такий приклад, щоб він починався з числа відповіді попереднього прикладу і т. д.
Останній учень складає такий приклад, щоб його відповідь співпадала з першим числом початкового приклада.
![]()
![]()
![]()
![]() Варіант А. можна писати на листочках, дошці, великому аркуші паперу.
Варіант А. можна писати на листочках, дошці, великому аркуші паперу.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 24 6
24 6
![]()
![]()
![]()
![]() 3 48
3 48
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 36 9 90 8
36 9 90 8
![]() 72
72
![]()
Варіант Б. Можна працювати в робочому зошиті. Записувати приклади треба повністю, щоб дати можливість для перевірки (самоперевірки, взаємоперевірки, фронтальної перевірки тощо). При ускладненому варіанті з творчим завданням шліфується техніка лічби, логіка мислення.
Диктант 8. «улюблене число»
Діти складають приклади так, щоб у відповіді вони отримали дане число. Число може обрати вчитель, учень-ведучий у групі, парі, трійці, класі. Це може бути дата проведення року, число, коли дитина народилися, число – день народження мами, просто улюблене число.
Це завдання дає простір для творчості, можливість індивідуалізації, організації роботи в парі, трійці. Кожен працює в міру сил і можливостей на певному рівні.
Під час підведення підсумків враховується кількість, різноманітність і правильність розв’язуваних прикладів.
Диктант 9. «Хто більше?»
Учитель дає формулу чи приклад-зразок, і діти за зразком чи формулою складають чи добирають якнайбільше прикладів і розв’язують їх.
Варіант А. Якщо працювати за прикладом-зразком, то біля приклада добре було б вказати формулу.
![]() Наприклад:
Наприклад:
![]()
![]() 1+1=2
1+1=2
![]()
![]() 1+2=3
1+2=3
1+3=4
Це свідчить про високий ступінь засвоєння матеріалу.
Варіант Б. Формул може бути декілька:
![]()
![]()
![]()
Це не ускладнює завдання, а вчитель легко виявляє, якого виду приклади учні ще не засвоїли.
Варіант В. можна давати приклади декількох видів. Учні їх розподіляють на групи-стовпчики та внизу вказують формулу.
Вправа стимулює творчий підхід до справи, поєднує теоретичні та практичні знання і навички.
Диктант 10. «Веселі трійки»
Учні діляться на трійки, і кожна трійка розв’язує приклади певного виду на спільному аркуші (але по черзі, щоб працював кожен!). хто швидше впорається – той і переможе.
Варіант А. Можна посилити творчу сторону завдання тим, що трійки самі ск4ладають самі складають завдання за певною формулою. Потім трійки міняються завданнями й виконують їх. Кожна трійка перевіряє те завдання, яке сама створила, і оцінює його.
Варіант Б. Щоб підсилити ігрову сторону, листки-завдання виготовлюють у форми будь-якого предмета. Листок-завдання розрізається на три частини, і всі частини розподіляються між учням класу. Діти, розв’язавши приклади, знаходять друзів по трійці, складають з частин ціле, перевіряють приклади, виправляють помилки.
Варіант В. Цей варіант можна ще ускладнити, і гратися стане цікавіше, коли підібрати малюнки, які потрібно класифікувати, і після виконання основної роботи запропонувати учням розподілити малюнки, які вони склали в процесі роботи в групі. Це можуть бути квіти, посуд, звірі, геометричні фігури. Малюнки підбирають на 1-2-3-4 теми. Їх потім ще використовують для словникового диктанту на уроці мови тощо.
![]()
![]()
![]()
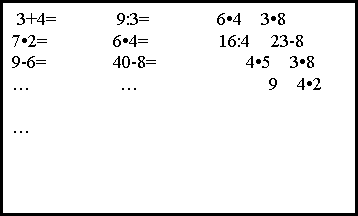
![]()
![]()
Диктант 11. «Геометричні фігури»
Кілька геометричних фігур розрізають на певну кількість частин і на кожній пишуть завдання. Хитрість у тому, що обирається різні фігури (диктант №11), або одна, але по-різному розрізана чи розрізана на різну кількість частин, можна ще змінити колір.
Варіант А. Розв’язавши приклади (задачі, рівняння), учень прикріплює свою частину фігури до дошки. Виграє та команда, яка швидше збере свою фігуру.

![]()
![]()



 Варіант Б (полегшений). Учитель на уроці обводить контури фігур (можна й місця розрізів) для зовсім маленьких дітей.
Варіант Б (полегшений). Учитель на уроці обводить контури фігур (можна й місця розрізів) для зовсім маленьких дітей.
Варіант В (ускладнений). Усі фігури однакові за формою чи кольором або і за формою, і за кольором – лише розрізані по-іншому. Можна розрізати на більшу кількість частинок. Додатково виміряти й обчислити P чи S фігури. Усе залежить від віку дітей.
Диктант 12. «Веселка»
Приклади на певну тему пишуться на картках іншим кольором. Учні розв’язують їх, а поті кожен прикріплюють на свою веселкову смужку, дібравши формулу. Райдуга-веселка засяє лише тоді, коли всі приклади (вправи, завдання) розв’яжуть правильно, і вони займуть відповідне місце. Формулу можна й не брати.
Варіант А(ускладнений). Учні розв’язують приклади, а поті самі добирають формули, класифікуючи завдання. Можна дібрати завдання так, щоб вийшов стовпчик з табличок додавання, множення.
Варіант Б . Якщо діти вже досить дорослі та самостійні, то кожен створює свою «веселку», тоді кількість прикладів у кожній смужці веселки можна зменшити, навантаження диференціювати.
Варіант В. Робота в парі. Спочатку діти створюють приклади, вписують їх у смужки веселки певним кольором, а далі міняються веселочками й працюють, а потім роблять взаємоперевірку (обсяг роботи зростає мінімум удвічі).
У кінці роботи можна буде підрахувати кількість «веселково прекрасних днів місяця» (за кількістю безпомилково виконаних робіт).
Формули добираємо відповідлно до програми. Якщо прослідковувається класифікація – це оговорюється. Наприклад: жовтим – табличка множення на «2». Пропонується продовжити до кінця.
Регулюється обсяг роботи, складність. Посилюється зв'язок теорії і практики. Учням-лідерам пропонують скласти й розв’язати задачу за прикладом з зірочкою.
На підставі цього диктанту-гри можна розгорнути цілий сюжетний ігровий урок.
Диктант 13. «Олімпійські ігри»
Учні отримують аркуш з 10-20 (50) прикладами, куди вони вписують відповіді. Виконуються перевірка, і аркуші розміщаються на Олімпі, відповідно до результатів.
Кількість прикладів залежить від віку дітей і виду роботи. Кожний щабель 1(2) бала – 100 метрів.
Ускладнення: опрацювати міри довжини – хто скільки кілометрів пройшов.
Перевести в кілометри. Дізнатися, скільки кілометрів пройшли всі разом. Хто піднявся найвище? Хто підкорив вершину Олімпу?

12 1200 м
11 1100 м
10 1000 м
9 900 м
8 800 м
7 700 м
6 600 м
5 500 м
4 400 м
3 300 м
2 200 м
1 приклад 100 м
Завдання допомагає учням закріпити знання мір довжини, уміння виконувати дії з іменованими числами.
Диктант 14. «Сходи»
Учням дають виконати завдання за певний час (приклади, вирази, рівняння, задачі). Як тільки час вичерпано, підводять підсумки. За результатами утворюють сходи.
На нижньому щаблі розміщується робота, із найменшою кількістю прикладів, на верхньому – з найбільшою. Переміг той, хто вирішив усі приклади й дістався до шкли (театру, лісу, басейну).
![]()
![]()
![]() Варіант А. Урізноманітнити диктант можна за рахунок сюжету (дійти до бібліотеки, комп’ютерного клубу, спортзалу). І буде цікавий місточок до наступного пункту плану уроку (чи наступного уроку взагалі).
Варіант А. Урізноманітнити диктант можна за рахунок сюжету (дійти до бібліотеки, комп’ютерного клубу, спортзалу). І буде цікавий місточок до наступного пункту плану уроку (чи наступного уроку взагалі).
![]()
![]()
![]()
![]() Школа
Школа
![]()
![]()
![]()
![]()
![]() 10
10
![]()
![]() 9
9
![]()
![]() 8
8
![]()
![]() 7
7
![]()
![]() 6
6
![]()
![]() 5
5
![]()
![]() 4
4
![]()
![]() 3
3
![]()
![]() 2
2
1приклад
Варіант Б. Приклади можна писати на сходинках, виготовлених дітьми заздалегідь, або давати готові сходи, куди діти вписують приклади і, обмінявшись картками, рахують їх.
Можна обіграти так, щоб кожний учень потрапив у своє улюблене місце.
Варіант В. «Ми зараз з вами побуваємо в багатьох цікавих місцях, куди запросили нас друзі, але щоб потрапити туди, треба пройти нелегкий шлях (виріши завдання). Дійшли? Пофантазуємо, що ми там побачимо, з ким зустрінемося, що будемо робити…» Таким чином учитель дізнається про смаки та схильності учнів класу.
Хто не зміг потрапити самостійно, тому допоможуть друзі (робота в парі). Перевірка – за підготовленими картками.
Диктант 15. «Хвилинка»
Дається хвилину часу, за яку потрібно вирішити якнайбільше завдань.
Варіант А. Учні самостійно обирають завдання із запропонованих.
Варіант Б. Усі отримають однакове завдання (на дошці чи картках).
Варіант В. Кожен удома готує завдання для друга, на уроці учні обмінюються ними та розв’язують.
Варіант Г. Працюємо в парі: один пише, а другий розв’язує, або по черзі. Аркуш можна розділити надвоє . Кожний на своїй стороні пише завдання, а потім обмінюється (для зручності аркуш розрізають), а можна запропоноване завдання виконувати в зошиті. Щоб не плутатись, де чиє завдання, учні пишуть завдання, учні пишуть завдання різною пастою: синьою, зеленою і т. д.
Добре видно обсяг роботи, який виконав кожен учень.
Варіант Д. Учні дають відповіді сигнальними картками, а учень-арбітр біля дошки фіксує правильно розв’язані завдання (відповіді відмічає зірочкою, рискою, кружечком…). Потім підраховують, скільки прикладів розв’язала гуртом за 1 хвилину. Можна знайти й середнє арифметичне (працездатність класу).
Рахуються лише ті приклади, які змогли розв’язати всі учні класу. Найкраще це видно, коли діти працюють з картками.
Диктант 16. «Ланцюговий»
Дається певна тема (формула, правило…), і учні за визначений час пишуть на обрану тему якнайбільше прикладів і розв’язують їх.
З прикладів на кожну тему складається «ланцюжок», і вчитель має змогу визначити, яку тему діти засвоїли й на якому рівні.
Варіант А. Теми може добирати як учитель, так і учень за власним бажанням (від 1 до 5 тем одночасно).
Варіант Б (спрощений). Учень отримує картку і прораховує «ланцюжок».
![]()
![]()
![]()
![]() 16 : 2 • 3 – 4 : 5 • 7 : 2 – 10 + 14 :3 :2 •7 +21 =
16 : 2 • 3 – 4 : 5 • 7 : 2 – 10 + 14 :3 :2 •7 +21 =
Диктант 17. «Футбол»
Учень пише на дошці два числа. Діти мають розподілити дані приклади відповідно до числа-відповіді. Якщо приклад розв’язано правильно, то вважається, що учень забив гол. Команда, яка забила більше голів, перемагає в матчі.
Варіант. Приклади можна придумувати. Хто більше придумає і запише прикладів, той і переміг у грі.
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]() Змагатися можна індивідуально, у парі, командами.
Змагатися можна індивідуально, у парі, командами.
Диктант 18. «Зебра»
До кожного приклада на 6 учень добирає обернений на – ( - на +, х на :; : на х). Приклади можна писати на дошці, у зошиті, на картці.
Завдання можна давати всім однакове чи диференціювати за обсягом і ступенем на картці.
Картка заповнюється «через рядок».
![]()
![]()
![]() 9 + 2 = Обернені приклади вписуються учнем пастою
9 + 2 = Обернені приклади вписуються учнем пастою
іншого 11 – 9 = кольору, і виходить «зебра».
Учні можуть працювати в
7 • 4 = парі – спочатку готують картки один одному, потім
… міняються і вписують обернені приклади.
14 - 6 = Взаємоперевірка!
![]()
![]() Диктант 19. «Віршований»
Диктант 19. «Віршований»
Швидко запишіть, малята,
Скільки буде – до 200 додати 600? 800
Ще 400 додайте 1 200
Й швидко відповідь вгадайте.
Суму поділіть на 100 12
Та й іще на два, 6
Всім вдалося?
Значить, у вас світла голова!
Десять разів візьміть по стільки 60
І на двоє розділіть, 30
А від того, що в нас вийшло,
Чотирнадцять відніміть. 16
А тепер оте число, що маємо, 4 • 4
На однакові добутки розкладаємо.
До одного з них ви 7 додайте 4 + 7 = 11
І відповідь-оцінку прочитайте.
Ледарів немає в нас?
Молодці, 4-й клас!
Варіант. Записуються тільки відповіді, а можна й усі приклади по порядку чи ланцюжком.
Матеріал до віршованих диктантів є в методичках і періодиці в достатній кількості, або самі проявляйте творчість. Вірші можуть скласти й учні, тоді виставляються дві оцінки: за приклади та за складання віршика (творча робота з мови).
Диктант 20. «Знаки, що загубилися»

![]() На картках, дошці чи в зошиті записано низку прикладів, а учні повинні вставити знаки (+, - ,•, :). Можна додати рівності й нерівності та ввести знаки >, <, =.
На картках, дошці чи в зошиті записано низку прикладів, а учні повинні вставити знаки (+, - ,•, :). Можна додати рівності й нерівності та ввести знаки >, <, =.

Диктант 21. «Числа порівняй. Знаки вставляй»
Учням пропонують скласти приклади (вирази) для диктанту, використовуючи знаки < чи >.
Наприклад.
Напишіть число, яке на 3 менше від 42; більше 8 в 7 разів.
Варіанту запису:
а) 42 – 3 = 39; 39 < 42 на 3;
б) 56 > 8 в 7 разів; 8 • 7 = 56. Диктант може диктувати й учень- ведучий, і вчитель. Якщо диктує вчитель, то учні можуть вставляти знаки в готові вирази, писати на слух чи з дошки.
Диктант 22. «Математичний віночок»
Кожен учень отримує квіточку з низкою прикладів (у системі чи просто так). Учні розв’язують їх (індивідуально чи в парі) і після правильного розв’язання і перевірки квітку вплітають у віночок.
Щоб до віночка вплести стрічечку, треба додатково розв’язати ще й ланцюжок прикладів.
Потім віночки можна обіграти на цьому ж чи на наступному уроці.
 а) вписати відповіді: б) вписати приклади:
а) вписати відповіді: б) вписати приклади:




![]()

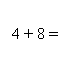


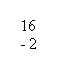

![]()
![]()



![]()

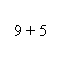











![]()



 в) вставити знаки:
в) вставити знаки:
![]()
![]()
![]()
Варіант А. На кожний ряд (групу) дати певний вид квіточок і плести різні види віночків (з ромашок, незабудок…). Можна, щоб квіти відрізнялися кольором.
Варіант Б. Віночки з різних квітів для кожного ряду плюс стрічки. Змагання: хто швидше сплете віночок.
Різнокольорові віночки радують око. До дошки квіти віночка кріплять магнітами, а до паперу – скетчем чи клеєм (олівець чи ПВА).
Диктант 23. «Ряд натуральних чисел»
Учитель диктує учням завдання, подібні таким чином, щоб у 1-му завданні відповідь була – 1 (одиниця), у другому – 2 і т. д.
Числа-відповіді зростає, утворюється відрізок натурального ряду чисел.
Наприклад.
- Що отримаєш у відповіді , коли ділене дорівнює дільнику?
- Було 18 горіхів. Кожен хлопчик узяв по 9. Скільки було хлопчиків?
- В ангарі 21 літак. 18 залишилося після того, як декілька злетіло. Скільки літаків злетіло в небо?
- Знайдемо х у рівнянні 16 : х = 4.
І так само далі…
Варіант. Можна просто використати приклади.
Звісно, це буде не так цікаво! Уже десь після 4 – 5 прикладу діти встановлюють закономірність і готові продовжити ряд чисел, дотримуючись порядку. Виграє той, хто зможе вивести формули натурального ряду:
![]() 1, 2, 3, 4, 5, … а + 1
1, 2, 3, 4, 5, … а + 1 ![]() ,
,
![]() або
або ![]() 2 (+1); 3 (+1); 4 …
2 (+1); 3 (+1); 4 … ![]() .
.
![]() - епсилон (безкінечність).
- епсилон (безкінечність).
Можна перевірити закономірність за допомогою звичайної лінійки, навчивши дітей рахувати «по лінійці».
Диктант 24. «Сусіди»
Напиши сусідів числа (хто живе справа, зліва, … через 1 квартиру зліва, через 2 квартири від числа, що є відповіддю в прикладі…).
![]()
![]()
![]() Варіант А.
Варіант А.
… 4 … , … … , … …
![]()
![]() Варіант Б.
Варіант Б.
![]()
![]() . ;
. ;
![]()
![]() . . .
. . .
![]()
![]() ;
;
Диктант 25. « Візерунки, або Орнамент»
 Дітям дають на вибір геометричні фігури з прикладами для розв’язання. Розв’язавши і розташувавши фігури в порядку збільшення (чи зменшення) відповідей, учень отримує певний візерунок – орнамент з геометричних фігур.
Дітям дають на вибір геометричні фігури з прикладами для розв’язання. Розв’язавши і розташувавши фігури в порядку збільшення (чи зменшення) відповідей, учень отримує певний візерунок – орнамент з геометричних фігур.



![]()
![]() 2 4 6 9
2 4 6 9
![]()


Якщо відповіді писати із зворотної сторони, буде легше утворювати орнамент.


![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Варіант А. Можна зробити цікавіше. Дати квадрат-матрицю, вкласти фігурку у квадрат із відповіддю та отримати візерунок. Фігурки однакові ( , , ), але відрізняються кольором, а можуть бути й різні.




![]()
![]()
![]()


![]()
![]() 2 3 4
2 3 4
![]() 5 6 7
5 6 7
![]() 8 9 10
8 9 10
Варіант Б. Можна дати шифр : Розв’язати приклади й розфарбувати фігурку з відповіддю 6, 11, 21, 4, 30 – блакитним кольором. Вийде візерунок.
Учитель має матрицю для швидкої перевірки.
Диктант 26 . «Квітковий»
Діти отримають «пелюстки» з прикладами. На кожній пелюстці – один складний приклад чи ланцюжок. На дошці прикріплюються серединки квітів з числом-відповіддю. Виконавши завдання, учень прикріплює пелюсточку до відповідної серединки-відповіді. Виграє п’ятірка, яка швидше виростить (збере) свою квітку.
Можна все зробити на плакаті (папері) й тоді чудовим букетом чарівних квітів привітати батьків після уроків (чи зі святом)
Варіант А. Підготувати для кожного учня аркуш паперу з «букетом» квітів. 5 днів тижня – 5 квіточок. Щодня «збираючи» одну квітку, у кінці тижня отримуємо букет квітів.
Варіант Б. Щодня заповнюється одна квітка, але на пелюстках пишуться різні завдання:
1 пелюстка – диктант;
2 - рівняння;
3,4 – задачі;
5 – логічні завдання.
Весь урок можна працювати на пелюстках квіточок, а потім зібрати квіточку й скласти букет (один чи декілька).
Пелюстки беруть кольорові або потім їх розфарбовують за вказівкою вчителя.
Варіант В. Можна влаштовувати «квітковий день»:
- Квіточка – для уроку математики;
- Квіточка – рідна мова (тест, завдання, правило…);
- Квіточка – читання (тест, загадки, прислів’я …);
- Квіточка - …;
- Квіточка - …;
Так, у кінці дня в нас вийде букет чарівних квітів.
На листочках – додаткове завдання для ерудитів. Математика + малювання (елемент інтегрованого уроку). І море задоволення! І блискучий результат!
Диктант 27. «Лічу двійками (3, 4, 5, 10…)»
Перший учень називає число 2, другий – 4, третій – 6 і т. д. Учні записують рядок, роблять висновки. Сильні учні не чекають решту й пишуть само-диктант.
Діти рахують: 2 (3, 4, 5, …) – скільки зможуть (скільки дітей у класі) або 1-й ряд рахує «2», 2-й – «3», 3-й ряд – «4» тощо… Можна диференціювати завдання за складністю і ділити дітей на групи, пари… Під час перевірки учні фактично повторюють усі завдання, ніби ще раз усно виконують їх.
Дуже корисний вид роботи під час вивчення таблички множення.
Варіант. Додати гру «Мовчанка», учні записують ланцюжок відповідей, а поті, помінявшись зошитом з сусідом, перевіряють його роботу.
Коли завдання різні, то учень фактично виконує подвійну роботу й повторює два стовпчики таблиці.
Диктант 28. «Табличний»
Знайди «ключ», заповни пропуски:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а)
а)
б)
1 ряд – парні від двійки;
2 ряд – числа від 1 по порядку;
3 ряд – сума чисел стовпчика.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() в)
в)
a – збільшується на 3;
b – зменшується на 1.
Варіант підбирають будь-які, відповідно до теми й мети уроку.
Учитель слід мати матрицю для перевірки. Картки можуть бути різні й однакові.
Диктант 29. «Математичний годинник»
На дошці кріплять годинник з прозорою кишенькою. У кишеньку вставляють знак, і учні розв’язують приклади, які задає вчитель, записуючи лише відповіді.
Чорна стрілочка вказує на перше число прикладу, біла – на друге.
Диктант можна не писати, а відповіді показувати сигнальними картками чи за допомогою математичного віяла.
Якщо вистачає циферблатів, можна працювати в парі, трійці…
Диктант 30. «Загадковий»
(з логічним навантаженням)
-
 Як з 3-х одержати шістку? (III VI.)
Як з 3-х одержати шістку? (III VI.)
- Запиши всі 2- цифрові числа, в яких сума десяткові і одиниці дорівнює 5 (14, 23, 32, 41, 50.)
- Добуток яких трьох чисел дорівнює їх сумі? ( 1 + 2 + 3 = 1 • 2 • 3.)
- З трьох п’ятірок склади вираз із відповіддю 0. (5 • ( 5 – 5) або (5–5):5.)
-


 Яке число зменшиться на 12 (21, 33), коли аркуш перевернемо догори ногами? 98 86 (на 12);99 66 (на 33); 89 68 (на 21).)
Яке число зменшиться на 12 (21, 33), коли аркуш перевернемо догори ногами? 98 86 (на 12);99 66 (на 33); 89 68 (на 21).)
- Ціпок має 2 кінці, а скільки кінців у половини ціпка? (Теж 2.)
- У чотирикутника обрізали кут. Яка фігура вийшла? (П’ятикутник.)
-



 З п’яти паличок склади 2 трикутники. ( 1 .)
З п’яти паличок склади 2 трикутники. ( 1 .)
![]() Відповіді діти записують у зошит, після закінчення роботи диктант аналізують гуртом, коментуючи незрозуміло. Завдання для диктанту можуть добирати й самі діти (за бажанням чи завданням учителя).
Відповіді діти записують у зошит, після закінчення роботи диктант аналізують гуртом, коментуючи незрозуміло. Завдання для диктанту можуть добирати й самі діти (за бажанням чи завданням учителя).
Такі завдання сприяють розвитку логічного мислення.
Диктант 31. «Задачний»
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Учням пропонують 5 – 10 нескладних задач. Вони розв’язують їх усно, а відповіді записують до зошита чи картки.
Учням пропонують 5 – 10 нескладних задач. Вони розв’язують їх усно, а відповіді записують до зошита чи картки.
Варіант А. На дошку вивішуємо 5 – 10 опор для складання і розв’язання задач.
Якщо йде робота в парі, то ведучий складає і розв’язує обернені до даних задачі, а ведений – просто розв’язує запропоновані та записує відповіді.
Одна задачу дають під запис.
Варіант Б. Робота гуртом: діти (за бажанням) піднімають руку та розв’язують 1-шу із запропонованих задач, наступний – складає і розв’язує обернену, (можна тільки скласти, а розв’язувати буде інший учень).
У вчителя є матриця з усіма можливими варіантами задач.
Диктант 32. «Комп’ютерщик»
 Бажано грати на комп’ютері.
Бажано грати на комп’ютері.


![]()
![]()

![]()


![]()
![]()
![]()
Це зразок, але можливі безліч інших варіантів.
Діти – оператори ЕОМ – працюють на комп’ютері (можна уявному), розв’язують приклади на швидкість.
Кращому – присвоюють звання «Комп’ютерщик екстра-класу».
Диктант 33. «Вибірковий»
Кожен отримує таку картку та завдання: «Вибери й обведи приклади на додавання (множення, ділення, віднімання) з відповіддю 12 (16, 11 , 14, …)»

![]()
![]()
![]()
![]()
![]()
![]()
![]() Задачу можна ускладнити: приклади з відповіддю 12 – обвести червоним, а з відповіддю 11 – зеленим тощо. Переможе той, хто знайде найбільше варіантів.
Задачу можна ускладнити: приклади з відповіддю 12 – обвести червоним, а з відповіддю 11 – зеленим тощо. Переможе той, хто знайде найбільше варіантів.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Знайдемо приклади записують;
9 + 3 = 12 2 + 4 + 6 = 12 4 + 6 + 2 = 12
Диктант 33. «Лучники»
Кожен отримує картку-мішень, треба стрілою влучити в ціль (відповідь).
![]()
 10 прикладів – 10 очок, якщо немає помилок.
10 прикладів – 10 очок, якщо немає помилок.

Якщо картки однакові, то вибираємо 3 – 4 судді-арбітра для їх пе6ревірки. Учитель перевіряє перші 3 – 4 картки. Якщо картки різні, то кожен арбітр – 5 карток максимум. Перевірена картка з оцінкою 10 балів дає учневі право теж стати суддею- арбітром і допомагати перевіряти картки.
Арбітр допомагає учневі-лучнику виправити помилки тільки після 2-х невдалих спроб.
Перемагає той лучник, який пустив дві стріли в «яблучко», тобто розв’язав усі приклади. Приклади можна диференціювати за ступенем складності, тоді арбітрами зможуть побути навіть слабші учні. Це дає їм можливість самоствердитись, повірити у свої сили.
Диктант 35. «Намисто»
Диктант схожий на кругові приклади, але в цьому випадку дитина, знайшовши відповідь, сама складає наступний приклад. Намистинки розсипані по одній, і задача дитини – зібрати їх і називати.
Перший приклад – видно, далі учні працюють методом підстановки та логічних міркувань.
Варіант А. Позначається перша й остання намистинка. Намистинок не повинно бути більш п’яти, бо дуже важко буде порахувати всі можливі варіанти.
Варіант Б (спрощений). Дати готові намистинки, а діти просто рахують. Можна добирати форму та колір намиста, щоб було цікавіше.
Маємо відповіді 3, 6, 9, 14, 19, 22, 37, 56, 89, 100. Парні числа – круглі червоні намистинки, непарні – продовгуваті жовті.
Придумаємо за бажанням! У цьому випадку кількість намистинок може зрости в 2 – 3 рази до 10 – 15 штук.
Краще використовувати індивідуальні набори намиста.
Варіант В (ускладнений). Зі зворотньої сторони намистини пишуться літери якогось слова і, коли намисто зібране правильно – прочитується слово.
Учитель дає розсипані намистинки, а далі просить дітей розташувати числа в порядку зростання, а відповідно розташувавши, розфарбувати.
Варіантів можна підібрати безліч!
Диктант 36 «Мереживо»
2 • 4 - 5 + 6 : 3 + 7 • 10 : 50 =
1-й приклад: від 2 у кружечку по дужечках іти під числа до числа, повертаючись по колу знову до двійки.
2-й приклад: кружечок у центрі з’єднано з іншими кружечками. Множимо, а відповідь вписуємо в трикутники.
3 х 2 = 6
3 х 4 = 12
3 х 5 = 15
3 х 6 = 18
3 х 3 = 9
7 х 3 = 21
3 х 10 = 30
3-й приклад:рухаємося від квадратика з зірочкою. Складаємо за стрілочками числа і записуємо в трикутника:
12 + 15 + 18 + 9 + 21 + 3 + 150 + 6 =
Диктант 37. «Павутинка»
Диктант допомагає опонувати таблицю множення на 2, 3, 4, 5, … . Усе залежить від добору чисел у павутинці. Спочатку треба встановити секрет плетіння павутинки (по колу від найменшого до найбільшого числа чи навпаки). Бажано, щоб діти зробили це самостійно. А далі рахуємо і вставляємо числа. Хто вставив усі числа – той спіймав усіх мушок у свою павутинку.
Кількість кілець у павутинці диференціюється за рівнем і обсягом. За павутинкою зручно працювати й у парі. Тоді кількість кілець-завдань кратна 2. І кожен працює пастою свого кольору. За сигналом «павучки» починають роботу. Потім роблять взаємоперевірку. Павучок, який сплів павутинку раніше, отримує 1 бал бонусу за швидкість (якщо всі завдання виконано правильно). При взаємоперевірці учень перераховує два варіанти роботи.
Варіант (спрощений). Перше число кола позначаємо певним знаком чи кольором.
Допомагає закріпити табличку множення, зрозуміти секрет її будови.
Диктант 38. «Сніжинки»
На дошці чи аркуші паперу малюємо сніжинки. Можна 1 аркуш на 2 – 3-х учнів – це залежить від кількості сніжинок на ньому. Діти розв’язують приклади (кожний пише пастою свого кольору чи помічає свою сніжинку якимось умовним знаком).
Завдання: за певний час зібрати якнайбільше сніжинок. Підводять підрахунки й виявляють переможця.
Варіант «Метелиця». Учитель утворює в класі «метелицю», розсипаючи сніжинки-завдання по всьому класу – «сніг іде!»Діти ловлять лише по одній сніжинці1 Ніхто не має права взяти ще, поки не закінчить роботу з попередньою. Можна потім усі сніжинки зібрати в снігову кучугуру (замет). Але спочатку виявляють переможця. Сніжинки можуть виготовити й діти (вдома з батьками чи в позаурочний час у ГПД) на уроці праці чи малювання. Заготовка – квадрат чи коло.
Диктант 39. «Сузір’я»
З чисел та знаків-зірочок утвори, запиши та розв’яжи якнайбільше сузір’я .
Зірочка можна розташувати на дошці, картці чи давати набір – кожному свій (чи один на двох).
Варіант А. Учень-космонавт складає приклади на дошці, а учень записують і розв’язують.
Виграє той, хто здійснить найдовшу космічну подорож і відвідає найбільш сузір’їв.
Варіант Б. Можуть змагатися два зоряні екіпажі (дошку ділять навпіл). Біля дошки працює капітан корабля (чи керує учнями, які по черзі працюють біля дошки). Екіпажі можуть складатися з 2-х, 3-х, 4-х чоловіків.
Головне в грі – визначити секрет, щоб не пропустити жодного прикладу: з кожного можна скласти ще 3!
3 • 8 = 24
8 • 3 = 24
24 : 3 = 8
24 : 8 = 3
Щоб перемогти, треба пригадати (розгадати) секрет утворення прикладів у таблиці та переставний закон множення чи додавання тощо.
Варіант В. Можна складати не тільки прості приклади, а й складні, а також рівності та нерівності…
4 • 3 + 12 = 36 : 6 > 8 : 4
6 • 2 + 24 = 6 • 4 + (3 + 9) =
У відповіді повинно вийти одне з даних чисел. Додавати інші (яких немає на зірочках) – не можна! Виграє екіпаж, який створив (знайшов) найбільше та найкрасивіше сузір’я .
Диктант 40. «Листопад»
Діти принесли восени з прогулянки купу різнокольорового листя. Чудово!




![]()
![]()

![]()
![]()
![]() Пам’ятаєте нашу «метелицю»? А тепер у нас буде справжній листопад. Беремо маркер і на яскравих жовтих листках клена пишемо числа та знаки. А далі – граймося! (У класі, парку, у спортзалі…). Складаємо «живі приклади», розлившись на групи-команди по 5 учнів:
Пам’ятаєте нашу «метелицю»? А тепер у нас буде справжній листопад. Беремо маркер і на яскравих жовтих листках клена пишемо числа та знаки. А далі – граймося! (У класі, парку, у спортзалі…). Складаємо «живі приклади», розлившись на групи-команди по 5 учнів:
У класі листя можна кріпити до дошки, розсипати по підлозі, а діти вибиратимуть потрібне та складатимуть приклади. І тоді на дошці хаос листопаду поступово перетвориться на логічну побудову математичних прикладів.
Варіант А. Виростимо дерева.
Разом чи окремо (самостійно, у парі, групі).
Коли деревце «виросло», можна запропонувати дітям виписати приклади з певним множником (дільником, доданком тощо). Чи на додавання, на віднімання, ділення. Якщо деревце було намальоване на аркуші паперу, то його до оформлюють на уроках праці, малювання чи в ГПД і створюють панно чи стіннівку.
Листочки висихають і поступово скручуються, а діти, спостерігаючи. Вчаться ще й досліджувати, аналізувати. Цей диктант-гру діти обожнюють! Крім знань він ще дарує їм стільки яскравих хвилин радості!
Варіант Б. Осіннє панно (чарівний килимок листопаду). Інтегрований урок математика – образотворче мистецтво. За допомогою такого панно не тільки добре опановуємо таблицю, а й робимо висновки, продовжуємо ряд, вставляємо пропущені числа та знаки, складаємо рівняння, вирази, задачі, порівнюємо їх … Усе залежить від матриці, яку створив учитель для зразків.
Варіант В. можна використати листя, яке малювали на уроках образотворчого мистецтва, чи вирізані аплікації, які готували для уроку в ГПД чи вдома з батьками. Але краще – справжнє!
Диктант 41. «Кульки»
Заздалегідь підготувати кульки, на яких написані приклади. Кульки парні6 на першій – приклад, на такій самій другій – відповідь до нього. Діти в процесі гри знаходять пари. Кульки можуть бути демонстраційні та роз даткові. Якщо кульки намальовані на дошці, то пари з’єднуємо ниточками-лініями.



![]()
![]()
![]()
![]()
![]()
![]() Вирізані кульки кріпляться до дошки магнітами чи скетчем. Можна намалювати кульки в певний колір.
Вирізані кульки кріпляться до дошки магнітами чи скетчем. Можна намалювати кульки в певний колір.
Варіант А (ускладнений). Кульки-приклади і кульки-відповіді мають різну форму.
Пари з’єднується стрілочками та розфарбовуються в однаковий колір.
Після цього створені приклади записують до зошита чи виписують певну групу (з добутком 24, дільником 3, ті, де відповіддю є парне число тощо).
Варіант Б. Під час КВК, свята чи просто гри малюємо приклади на справжніх кульках маркером (це залюбки роблять і діти), погратися ними, підкидаючи догори та один одному і спробувати (за сигналом) знайти свою пару-відповідь. І гра, і наука, і розвага! Така фізкультхвилинка: і нарадієшся, і настрибаєшся, і нарахуєшся!
Можна, щоб кульки підготували діти вдома: на 1-й кульці – приклад, на 2-й – відповідь.
Варіант В.Робота проходить у класі. Кожен приносить кульку, учні працюють у парі (ведучий пише приклад, а ведений на своїй кульці – відповідь. Кульками обмінюються під час гри, а за сигналом – утворюють пари.
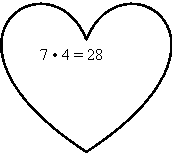

 Диктант 42. «Сердечка»
Диктант 42. «Сердечка»
Диктант-гра у формі веселої фізкультхвилинки. Необхідну кількість сердечок підраховують просто: кількість учнів ділять на 2. Якщо вона складає непарне число, то в одну пару з учнем стає вчитель. На кожному сердечку пишемо приклад так, щоб знак «=» був посередині. Сердечка розрізаємо надвоє і половинки розкладаємо в безладі на парті. Кожен бере собі половинку та шукає пару, щоб вийшов приклад. Учні вільно рухаються по класу, спілкуються. Створені приклади-сердечка прикріплюються на дошці, і дається певне завдання (списати, виписати, розташувати в певному порядку, розділити на 2 – 3 стовпчики тощо). Задача ускладнюється, коли всі сердечка однакові. Найкраще провести диктант на День Святого Валентина.
Диктант 43. «хмарочоси»
Учитель малює на дошці кілька прямокутників – закладає фундамент хмарочосів (пише початок таблиці або число-відповідь у прикладах тощо).
Учні зводять будинок, встановивши закономірність, розв’язують складені власноруч приклади, поступово переходять на «поза табличні» випадки.
Хто вибудує за певний час найвищий хмарочос, той і переміг.
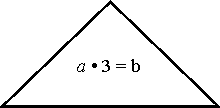

![]()
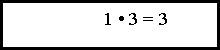
![]() Бонус тому, хто на даху хмарочоса напише формулу, за якою працював.
Бонус тому, хто на даху хмарочоса напише формулу, за якою працював.
Учні практично засвоюють порядок складання таблиці, визначають і узагальнюють секрети.
![]() Наприклад: 1-ше число a – не змінюється, постійне. Значить табличка буде на число a. Друге число b – виростає на 1. Значить число c щоразу виросте на число а. У пишемо, що це табличка на а. Робота дає змогу пояснити секрети поза табличного рахунку (лічби), навчитися швидко рахувати. Можна працювати на картках, біля дошки, у зошитах. Якщо хмарочоси виросли на дошці, то можна ускладнити завдання (не всім, а вибірково); скласти приклади-пояснення ось у такий спосіб (це може бути й фронтальна робота за зразком).
Наприклад: 1-ше число a – не змінюється, постійне. Значить табличка буде на число a. Друге число b – виростає на 1. Значить число c щоразу виросте на число а. У пишемо, що це табличка на а. Робота дає змогу пояснити секрети поза табличного рахунку (лічби), навчитися швидко рахувати. Можна працювати на картках, біля дошки, у зошитах. Якщо хмарочоси виросли на дошці, то можна ускладнити завдання (не всім, а вибірково); скласти приклади-пояснення ось у такий спосіб (це може бути й фронтальна робота за зразком).
Можна дати тільки 1-й приклад таблички в 1-й колонці.
Сильні учні виконують завдання в ритмі випереджуючи навчання.
Диктант 44. «Лабіринт»
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()














Завдання просте: знайти відповідь у переходах лабіринту. Буде, краще, коли кожний шлях до відповіді учень буде позначати іншим кольором.
Якщо приклади взяті з 1-ї таблички, то учні розставляють їх у певному прядку. Приклади добирають і на додавання, і на віднімання, і на ділення, це може бути рівняння, де треба знайти х. Переможе той, хто першим пройде лабіринт.
![]()
![]()
![]()
![]() Диктант 45 . «Дощ»
Диктант 45 . «Дощ»
![]()
![]()
![]()
Дібравши певний набір чисел-краплин, учням пропонується наповнити відерце цілющою дощовою водою, склавши й записавши приклади з відповіддю х (дивись на відерці). Хто перший набере води, той – переміг. Дозволяється використовувати тільки числа-краплини та знаки +, -, :, •, та =.

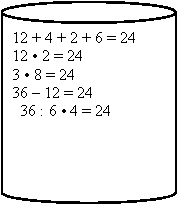 24
24
Відерець може бути 1 -5 штук чи в кожному учня своє. Після закінчення роботи (коли відерця із завданнями однакові) діти зачитують свої приклади, а решта дописує ті, яких немає, на відерце чи в зошит. Організовують взаємоперевірку, якщо кожний виконував свою роботу.
Відерце можна розфарбувати. Якщо відповідь – парне число, то одним кольором, непарне – другим, числа, що містять двійку – третім тощо.
Варіант. Закріплення складу числа. Удосконалення знань таблиці додавання.
Диктант 46. «Будівельник»
Спочатку побудуй будинок. Розмір цеглинок 1 х 2 клітинки. Висота – 10 клітинок, ширина – 20 клітинок. Під’їздів – 5.Далі заселяються перші мешканці (числа та знаки списуються зі зразка вчителя).
Варіант А. Числа вписуються дітьми в будиночок.
Варіант Б. Цеглинки-відповіді діти отримають у наборі та вкладають чи вклеюють їх на свої місця.
Продовженням роботи стає побудова цілого математичного містечка, учні наклеюють будинки на папір та розфарбовують їх. На папері заздалегідь роблять розмітку вулиць, скверів, парків тощо. Але це вже робота для уроку праці чи для занять у ГПД (елемент інтеграції.) Таким чином організовується цілий проект «Моє місто». Можна провести змагання будівельних бригад, конкурс «Золотий майстер» тощо (форма роботи індивідуальна, групова, парна чи фронтальна).
Диктант 47. «Сонечко»
До кола-сонечка добираємо промінчики-приклади, відповідно до вказаної відповіді. Промінці вирізаються окремо від сонечка. Їх потім просто прикладають чи приклеюють. Сонечко може бути одне на всіх (на дошці), чи в кожного своє, або й по 2 – 3.
Сонечка потім теж використовують в роботі: їх розфарбовують, створюють на основі сонечка аплікацію, організовують гру. За аплікацією складають розповідь. Можна використати його й для проекту «Моє місто» або просто приклеїти до аркуша паперу й провести «сюжетне малювання»:»Про що мені розповіло сонечко» чи «Сонячний день (ранок)». Якщо перегорнути сонечко на другий бік, то можна використати його для гри-теста «Який я» (див. «Щоденник розвитку особистості учня початкової школи» Павленко Л. П.).
![]() Промінці заповнюють діти (батьки, учитель).
Промінці заповнюють діти (батьки, учитель).

![]()
![]()
![]()

![]()
![]()
![]()

![]()
Не тільки лічбу вивчаємо, а й про себе розповідаємо.
Диктант 48. «Равлик»
Закріплюємо таблицю множення (чи додавання, віднімання, ділення). Рахуємо усно, а вписуємо лише відповіді після першого множника. Дається «старт» і равлики «рухаються» до «фінішу».
За сигналом «стоп» кожний відмічає, де зупинився. Чий же равлик переміг? Фігурку равлика також можна буде використати для уроків малювання, гри, проектів «Моє місто» чи «Рідна природа».
Диктант 49. «Учитель»
Якщо зібралося чимало карток з виконаними завданнями, можна спеціально залишити кілька комплектів неперевірених. Картки роздають дітям, і вони перевіряють їх, виправляючи помилки. Ставлять оцінку. Вони ж це так люблять!
Варіант. Якщо картки з помилками готуються спеціально, то слід скласти приклади так, щоб перше число першого прикладу показувало кількість помилок, допущених у роботі навмисно. Так учителеві легше буде перевіряти.
Кількість прикладів – 10 – 15, помилок – до 10. Серед прикладів обов’язково є такі, що розв’язані правильно. Вони – найважчі для розв’язку і їх корисно повторити (чи запам’ятати!). приклади підбирають на 1, 2, 3, 4 дії.
Диктант 50. «Ескалатор»
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Сходи ескалатора діти малюють самостійно за вказівкою вчителя (графічний диктант). Учитель диктує: спускаємося вниз на 10 клітинок. Від лівого краю відступаємо 1 клітинку та рахуємося вправо на 3, знову піднімаємося на 1 вгору, на 3 ідемо вправо, 1 вгору, 3 вправо… Спиняємося, коли дійшли до правого краю зошита.
Сходи ескалатора діти малюють самостійно за вказівкою вчителя (графічний диктант). Учитель диктує: спускаємося вниз на 10 клітинок. Від лівого краю відступаємо 1 клітинку та рахуємося вправо на 3, знову піднімаємося на 1 вгору, на 3 ідемо вправо, 1 вгору, 3 вправо… Спиняємося, коли дійшли до правого краю зошита.
1 • 3 = 3
Учитель пише перший приклад будь-якої таблиці (у нас на 3). Далі діти піднімаються сходами ескалатора й вписують наступні за порядком. Спускаючись, пишуть під сходинкою зворотній приклад на ділення.
Можна ускладнити задачу й писати по 2 приклади, міняючи множники місцями (тоді й обернених на ділення буде 2). 2 приклада зверху й 2 знизу. Картку виготовлює вчитель чи діти (з батьками, учителем) завчасно. Форма роботи індивідуальна чи парі. Вид перевірки – взаємо- чи самоперевірка.
Диктант 51. «Сімейки»
Вправа-гра з відомою «сімейкою» прикладів.
Варіант А. З кожного прикладу складаємо ще 3. Виходить «сімейка». Прикладів беремо 3 – 5. Одночасно біля дошки працюватиме стільки учнів, стільки є груп.
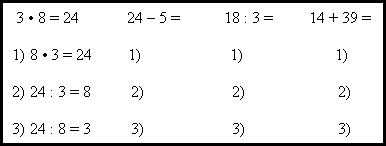
![]()
![]()
![]()
![]()
![]()
![]() Варіант Б. Приклади пишуть на картках-опорах. Слабким учням можна дати й набір прикладів-відповідей з «сімейок». Вони лише вкладають їх у відповідну колонку. Приклади з «сімейки» розрізати по одному. Працюють у парі, трійці, за варіантами.
Варіант Б. Приклади пишуть на картках-опорах. Слабким учням можна дати й набір прикладів-відповідей з «сімейок». Вони лише вкладають їх у відповідну колонку. Приклади з «сімейки» розрізати по одному. Працюють у парі, трійці, за варіантами.
 Диктант 52. «Терези»
Диктант 52. «Терези»
![]()
![]()
![]()
![]()


![]()

![]()
![]()
![]()
Закріплюємо таблицю мір маси.
Варіант А. Щоб урівноважити терези, треба дібрати відповідні грі. Можна вписувати числа, або вставити картку з набору, що дав учитель
Варіант Б. Переплутані відповіді вписані в картки, діти з’єднують правильні відповіді – урівноважуючи гирьки терезів.
Прикладів 5 -10, варіантів карток – за бажанням.
Учитель обирає арбітрів-помічників для перевірки робіт і визначення переможців.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Диктант53. «Сюжетний»
Варіант А. Семен вийшов з дому в ліс за грибами. Дорогою зустрів Катрусю і Дмитрика. Разом вони зібрали по 15 грибочків кожний. 20 грибків діти віддали на піццу, а рештою пригостили 5 білочок у міському парку. Білочки з’їли грибочків порівну. Скільки грибочків дісталося кожній білочці?
Запис задачі:
[15 • (1 + 2) – 20] : 5 = 5 (г.)
Запис ланцюжка:
1 + 2 • 15 – 20 : 5 = 5.
Легше записувати у вигляді ланцюжка, бо тоді дитина одразу працює в процесі розгортання сюжету.
Учитель читає двічі. Перший раз для ознайомлення, а другий – у процесі виконання роботи.
Коли диктант проводиться вперше, то можна коментувати (підказувати, аналізувати), усі кроки роботи, наводити зразки.
Варіант Б. На подвір’ї гуляло 18 хлопчиків і стільки ж дівчаток. Після того, як команда по 6 чоловік пішли грати у волейбол, а половина з решти стали грати в класики, ті діти, які залишилися, розділилися порівну і стали поливати: 1- ш група – дерева, 2-га – кущі, а малюки – квіточки, щоб у дворі було гарно та красиво. Скільки малюків поливає квіточки, якщо до них приєдналися ще близнюки Галя і Віра?
Запис задачі:
[(18 + 18) – 6 • 2) : 2] : (1 + 1 + 1) + 2 = 6 (д.)
18 + 18 – (6 • 2) : 2 : (1 + 1 +1) + 2 =6.
Можна не записувати, а розв’язувати усно чи записувати лише кінцеву відповідь (остаточний результат).
Сюжети складають і самі діти вдома, у ГПД, на перерві, на уроці.
На прогулянці, під час уроку тощо обігрувати реальні ситуації. Це стимулює розвиток творчості, логічного мислення.
Диктант 54. « Три числа»
Учитель називає три числа, а учні складають з ними всі можливі приклади. Брати інші числа чи заміняти їх – не можна.
Варіант А.
![]()
![]()
![]()
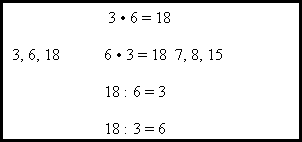
Варіант Б. Нехай учні самостійно розв’язують чарівні трійки чисел, відшукавши «ключ-розгадку» складання прикладу. Під час роботи в парі слід давати різні види прикладів: на + та - ; на : та х. Лише коли відпрацьовується система роботи в парі : ведучий – ведений, то дають приклади однакового плану, щоб ведений, впорався з роботою за зразком. Можна давати схожі, але з різними числами приклади тощо.
Диктант 55 «Снігові намети, або Купа мала»
За завданням учителя діти поширюють простий приклад, утворюючи «ланцюжок». На дошці (картці, зошиті) учитель (учень) пише число або простий приклад, а далі його поширюють. Чим довше – тим цікавіше. Добре було б використовувати й дужки. Чи знаки <, >. =.
 Варіант А.
Варіант А.
![]() 32 : 4 + 8 : 4 • 3 – 6 : 3 …
32 : 4 + 8 : 4 • 3 – 6 : 3 …
Варіант Б.
- 32 :4 =
- 32 : 4 • 5 =
- 32 : 4 • 5 -12 =
- (32 : 4 •5 – 12) : 2 =
- …
Форма роботи – фронтальна, у групі, парі, диференційована. (Вид перевірки залежить від виду роботи.)
Диктант 56. «Ялинки»

 Завдання: якнайшвидше запалити вогники га ялинці (розв’язати всі приклади, вписані в ліхтариках-кружечках).
Завдання: якнайшвидше запалити вогники га ялинці (розв’язати всі приклади, вписані в ліхтариках-кружечках).
 Варіант А.
Варіант А.




![]()


![]()



![]()


![]()


![]()
На ялинці пишуться приклади, а учень добирає відповідь і вкладає (вписує, вклеює) у відповідний кружечок. Відповіді бажано писати на кольорових кружечках, щоб ялинка була красивішою.
Варіант Б.
![]()


![]()

![]()


![]()

![]()

![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
Навпаки: на ялинці написані в кружечках відповіді, а добираються приклади.
Розташування прикладів:по краю, хаос, гірляндою. Ялинка може бути одна (на дошці), одна на двох (у парі), у кожного своя, одна на групу дітей.
Проводять і змагання, хто швидше засвітить усі ліхтарики на ялинці. Зараховуються лише правильні відповіді. Кількість ліхтариків на картках – однакова, але можна диференціювати завдання за ступенем складності. Сильним дітям пропонують прикрасити ялинку додатково (іграшками, сніжинками). Якщо до ялиночок прикріпити скріпки чи петельки з ниточок, розфарбувати (якщо вони зроблені не з кольорового паперу), ними можна буде прикрасити новорічну ялиночку в класі, у парку. З ялиночок виготовляють гірлянди, а ще – новорічну стіннівку, панно. Сюди ж можна додати і сніжинки, зроблені раніше. І знову вийде багато цікавих уроків, ігор, розваг. За кращу сніжинку, ялинку – подарунок-приз вручать Дід Мороз та Снігуронька. Переможець отримує листівку від Дідуся, запрошення на Новорічне свято або диплом переможця.
Ялинки можна використати й для проекту «Моє місто». Написавши новорічне вітання, подарувати другу, мамі, татові, бабусі, дідусеві, учительці.
Диктант 57. «Серпатин»
На ялинці пишуть одночасно й приклади, і відповіді. Учні відповідно їх з’єднують і отримають низку серпантину. Якщо домовитись, що приклади на +, - з’єднуватимуться одним кольором, на х та : - іншим, то серпантин вийде різнокольоровим, а ялинка – ошатнішою. Приклади – кругові.
Ялинки використовуємо так, як і в попередньому диктанті.
Диктант 58. «Зайчик петляє»
Зайчик тікає від вовка. Врятує зайчика. Щоб зробити стрибок, треба розв’язати приклад. Розв’язавши низку прикладів і отримавши відповідь, дізнаємося, за скільки секунд зайчик утік від вовка.
Цей аркуш потім використовують для сюжетного малювання, гри, панно, проекту « Моє місто», проекту «Рідна природа». Цікаво дізнатися, що, тікаючи, зайчик заплутає сліди, петляє.
Диктант 59. «Велотрек, або Дужки»
На дошці (картці, зошиті) 10 прикладів з відповідями. Завдання: розставити дужки, щоб відповідь стала правильною:
Варіант А. Один учень працює біля дошки, решта – у зошитах.
Варіант Б. Усі працюють у зошитах. Хто перший впорається, той іде працювати до дошки – розставляти дужки.
Варіант В. Учитель диктує приклади по одному, учні записують у зошит і розставляють дужки. Хто перший впорався – отримує фішку. Кожний приклад – перший етап велогонки. Етапів може бути 5 – 10, лідери велогонки отримують фішку – майку лідера. У кого фішок більше – той переможець змагань.
9 • 6 – 4 = 18; 72 : 3 • 3 = 8; 100 – 4 • 9 : 8 = 8.
Диктант 60. «Рівняння»
Придумати й розв’язати 5 – 110 рівнянь із заданим невідомим для обох, або різним.
 Якщо змагання іде на дошці, то записують рівняння в стовпчики (хлопчики – дівчатка), у 3 стовпчики – по рядах, в 1 – по черзі, чи хто перший придумає. Працюють у зошиті, коли учитель диктує для запису; хто перший впорався – коментує. Учні можуть не записувати вираз, а лише значення невідомого.
Якщо змагання іде на дошці, то записують рівняння в стовпчики (хлопчики – дівчатка), у 3 стовпчики – по рядах, в 1 – по черзі, чи хто перший придумає. Працюють у зошиті, коли учитель диктує для запису; хто перший впорався – коментує. Учні можуть не записувати вираз, а лише значення невідомого.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а)
а)
![]()
. . . . . .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() б)
б)
![]() … …
… …
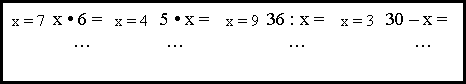
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() в)
в)
Диктант 61. «Будь-яке число вставляю, а відповідь правильну маю»
Діти записують приклади, що відповідають даній умові. Добре, коли зможуть класифікувати їх за групами (за формою).
Варіант А. На дошці (у зошиті, на картці) записують кілька формул і до кожної потім добирають 5 – 10 прикладів. Форма роботи – гуртом, групами, у парі.
Варіант Б. Ведучий диктує формулу – ведений складає приклад.
Варіант В. Кожному ряду (групі, варіанту) дається формула, і вони намагаються придумати за нею найбільшу кількість прикладів.
Варіант Г. Учні просто пишуть приклади, що відповідають умові (з використанням іменованих чисел).
Формули:
a – a = 0; a : а = 0
a + 0 = a; а : 2 = ½ а;
a – 0 = a; а : а = 1;
a • 0 = 0; а • 1 = а
0 : a = 0; …
Диктант 62. «Цифроманія»
Складання, запис і читання багатозначних чисел.
Дається одна чи кілька цифр і пропонується скласти щонайбільше чисел, записати їх, позначити класи, розряди й прочитати.
Домовитись, чи можна, щоб цифри в числі повторювалися:
а) 1, 11, 111, 1111, 11 111, 111 111, 1 111 111;
![]() б) 3, 4, 6, 346, 364, 436, 469, 634, 643;
б) 3, 4, 6, 346, 364, 436, 469, 634, 643;
![]() в)5, 7 57, 75, 77, 55, 575, 757, 577, 755…;
в)5, 7 57, 75, 77, 55, 575, 757, 577, 755…;
г) у числі 111 111 – 11 111 десятків, 1 111 сотень, 111 тисяч;
д) у числі 111 111 – 1 одиниця класу одиниць, 1 десяток класу одиниць, 1 сотня класу одиниць, 1 одиниця класу тисяч, 1 десяток класу тисяч, 1 сотня класу тисяч.
Можна також диктувати, скільки одиниць (тисяч) має бути в числі, а учні записуватимуть. Форма роботи – у парі. І далі за задумом учителя.
Диктант 63. » Заступник»
(різновид диктанту «Терези»)
Закріплення таблиці мір, маси, довжини, часу.
Учитель чи учень-ведучий диктують приклади. У парі диктують по черзі. Можна працювати в зошиті, на дошці, на картці, писати весь приклад (вираз) чи тільки відповідь.
Можна на час: хто більше встигне!
Ланцюжок – по одному до дошки чи передаючи картку.
Мета – замінити іменоване число тотожним йому, здійснивши перевод – тобто знайти число-заступника.
![]()
![]()
![]() 3 км 64 м 5 см = см;
3 км 64 м 5 см = см;
![]()
![]() 8 ц 3 кг = кг г;
8 ц 3 кг = кг г;
![]()
![]() 3доби 7 год 4 хв = хв.;
3доби 7 год 4 хв = хв.;
![]() 306 405 см = км м см.
306 405 см = км м см.
Диктант 64. «Більше – менше»
Порівняння іменованих чисел, перевод, закріплення мір довжини, ваги, часу.
Учитель диктує (пише) два іменовані числа (пару чисел), а учні (учень) вставляє між ними знак.
Краще запропонувати спочатку зробити перевод в одну величину для зручності в роботі.
Наприклад:
![]()
![]()
![]()
![]() 4 м 5 дм 3 см 4 м 5 см 3 мм
4 м 5 дм 3 см 4 м 5 см 3 мм
(4 530 мм) (4 053 мм)
Варіант (спрощений). Із більших величин отримати менші чи навпаки (перевести в м, км, см, дм, кг, т…0. Тобто з малих величин (см, мм) отримати більші (м, км) і т. д.
Для усного диктанту добирають легші приклади, для зорового – складніші.
Працювати можна дошці, картці, у зошиті, у парі, групі, по рядах.
Диктант 65. «Геометричний»
(розподільний)
![]()
![]() Не відриваючи руки й не проводячи двічі по одній лінії, малюємо конверт (а – 4 клітинки, b = 6 клітинок) .
Не відриваючи руки й не проводячи двічі по одній лінії, малюємо конверт (а – 4 клітинки, b = 6 клітинок) .
 С
С

 B D а = 4 клітинки
B D а = 4 клітинки
A K
в = 6 клітинки
Завдання полічіть кількість геометричних фігур у ньому (три-, чотири-, п’ятикутників).

![]()
![]()
![]()
![]()
![]() Можна окремо, а можна загальну кількість. Менші діти просто малюють фігурку-емблему, старші – пишуть назву фігурки. Форма роботи – фронтальна, у парі, групі, по рядах.
Можна окремо, а можна загальну кількість. Менші діти просто малюють фігурку-емблему, старші – пишуть назву фігурки. Форма роботи – фронтальна, у парі, групі, по рядах.
Диктант 66. «Геометричні тіла –
геометричні фігури»
Учень чи вчитель диктує (показує, прикріплює до дошки) назви фігур (саму фігуру), а учні змальовують (відмічають, розподіляють) їх у 2 колонки: плоскі та об’ємні. Фігури можуть бути виставлені на столі, дошці, парті, намальовані чи просто названі без демонстрації.
Учні працюють усно, біля дошки, на картці, у зошиті. Набір фігур залежить від класу (за програмою).
Мета завдання – вчити учнів розрізняти форму та назви геометричних фігур, класифікувати геометричні фігури та геометричні тіла.
Спосіб перевірки залежить від способу роботи учнів.
Диктант 67. «Магічні квадрати»
Розвиток логіки, мислення і навички додавання. У дані квадрати вставити числа так, щоб їх сума по горизонталі, вертикалі та діагоналі була однакова. Суму діти мають знайти самостійно.
Варіант А. Завдання ускладнюється тим, що квадрат діти креслять самостійно, а дані числа під диктовку вчителя діти вписують у квадрат за вказівкою:
- перший рядок згори зліва в кутку – 22. Справа 12;
- другий рядок середній квадрат – число 27;
- третій рядок правий кут – число 32.
![]()
![]()

![]()
![]()
 (Можливі варіанти зі стовпчиками, діагоналями.)
(Можливі варіанти зі стовпчиками, діагоналями.)
Магічне число – 81.
Учитель має матрицю з відповідями.

![]()
![]() Варіант Б.
Варіант Б.
![]()
![]()

![]()
![]()
![]()
![]()
 Варіант В.
Варіант В.
![]()
![]()
![]()
![]()

Диктант 68. «Площа та периметр»
Дано 5 – 10 геометричних фігур, треба знайти їх P чи S.
Фігури можна малювати на дошці, у зошиті, на картці чи давати готові (однакові чи різні всьому класу, для пари, трійки, ряду…).
Учитель дає параметри (розміри) фігур або пропонує дітям виміряти їх самостійно.
Варіант. Учень отримує фігуру, вимірює її розміри, а клас рахує і записує Р чи S (або те й інше). Далі фігуру отримає другий учень і т. д. Додаткове навантаження на сильного учня!
 Бонус отримає учень, який після диктанту напише формули, за якими можна ефективно працювати.
Бонус отримає учень, який після диктанту напише формули, за якими можна ефективно працювати.
![]() а) 12
а) 12
![]()
![]() 19 Р = ?
19 Р = ?
![]()
24

![]() б) Р = ?
б) Р = ?
![]() S = ?
S = ?
![]()

![]()
![]()
![]()
![]()
![]()
![]() в)
в)
![]()
![]()


![]()
![]()
![]() 1) 4 см 2) 2 см
1) 4 см 2) 2 см
 5 см
5 см

![]() 3 см
3 см
![]() 3) 7 см 4)
3) 7 см 4)
![]()
![]()
Варіантів дуже багато.
Учителю слід мати матрицю з відповідями для швидкої перевірки (чи залучити до перевірки помічників (учнів-арбітрів, ведучих у парі…).
Диктант 69. «Працівники ДАІ»
Визнач швидкість руху та напиши, хто (що?) рухається з такою швидкістю. Доведи, що не помилився.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() Закріплюється навички знаходження швидкості, правила дорожнього руху. Відповіді подано приблизно. Так по місту Vавт.= 60 км/год, за містом – 90 км/год, на швидкісній трасі – до 130 км/год.
Закріплюється навички знаходження швидкості, правила дорожнього руху. Відповіді подано приблизно. Так по місту Vавт.= 60 км/год, за містом – 90 км/год, на швидкісній трасі – до 130 км/год.
![]()
![]()

![]() и та класи»
и та класи»
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Варіант А. Учитель диктує числа, учні вписують їх у таблицю, читають, перевіряють.
Варіант Б. У таблиці вже є числа. Учню потрібно прочитати їх правильно в голос» 142 тисячі 563, або 1 сотня класу тисяч, 4 десятки класу тисяч, 2 одиниці класу тисяч, 5 сотень класу одиниць чи 1 сотня 4 десятки, 2 одиниці класу тисяч та 5 сотень, 6 десятків 3одиниці класу одиниць.
Варіант В. Учні по черзі диктують числа зі своїх таблиць (чи придумані), а решта записують у зошит через кому (можна накреслити табличку). Працюють індивідуально, у парі, групі, по рядах, фронтально. Біля дошки, за карткою, у зошиті, усно.
Диктант 71. «Тестовий»
Учням дають (диктують чи пишуть) низку завдань і 3 – 4 варіанта відповіді до кожного завдання на вибір.
Наприклад: 69 • 54 = ?
а) 4 500;
б) 7 946;
в) 3 726.
![]() 9 • 4 = 36, отже, число кінчається на 6. Їх у нас 2. Вибираємо далі 60 •50 = 3 000, значить, це число 3 726. Обводимо варіант .
9 • 4 = 36, отже, число кінчається на 6. Їх у нас 2. Вибираємо далі 60 •50 = 3 000, значить, це число 3 726. Обводимо варіант .
Для усного варіанту добирають легші завдання. Простіше, коли диктант – зоровий. Кількість завдань залежить від програми.
Диктант 72. «Підкорювачі вершин»
Діти записують чи називають 10 – 20 прикладів з однаковою відповіддю. Хто складе найбільше, той підкорив найвищу вершину (гору). Він матиме звання «найкращий альпініст».
Учні грають гуртом, групами, парами чи самі за себе.


![]()
![]()
![]()

![]() Картка для роботи в парі
Картка для роботи в парі
Гору можна назвати. Якщо диктант дається в 3 – 4 класі, то беруться найвищі вершини України (їх висота й буде відповіддю в прикладах), підписати на картці, на яку гору і хто піднявся, яку вершину підкорив). Виконуючи це завдання, діти вчаться ще й працювати з атласом (картою), знайомляться з природою України. Картку можна використати на уроках курсу «Я і Україна» під час вивчення тем «Карпати» та «Кримські гори». Це досить цікаво! Момент інтеграції корисний, і діти люблять такі завдання.
Диктант 73. «Ліфт»
Діти придумують і записують (або вибирають із запропонованих) приклади та розташовують їх у порядку збільшення чи зменшення відповіді. Оговорюється, що це будуть за приклади (на додавання, віднімання, множення чи змішення; прості чи складні) і на скільки збільшуватимуться чи зменшуватимуться відповіді (у скільки разів).
Домовляються, що числа мають бути одно-, дво- , трицифрові.
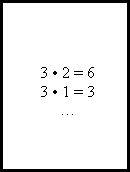
![]()
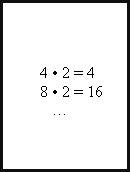
![]()
![]() Кабінку ліфта можна намалювати, вирізати, приклеїти.
Кабінку ліфта можна намалювати, вирізати, приклеїти.
![]()
Стрілочка показу, куди їде ліфт (звідки починати роботу).
Диктант 74. «Чарівники»
Числа-слова перетворити на цифри. Можна диктувати (учитель, учень, усі по черзі), або записати числа числівниками на дошці, картці чи в зошиті. Прикладів 10 – 20.
Наприклад:
а) п’ять тисяч вісімсот сім;
б) 6 сотень класу тисяч та 7 сотень 5 деків 3 одиниці класу одиниць.
![]()

![]()
![]() Картка
Картка
Диктант 75. «римські – арабські»
Римські замінюємо арабськими, арабські – римськими.
Варіант А. Учитель диктує, діти пишуть через тире: 7 – VII.
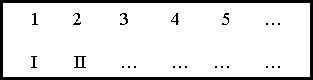
![]()
![]()
![]()
![]()
![]()
![]() Варіант Б. Дається картка:
Варіант Б. Дається картка:
![]()
![]()
![]()
![]()
![]() Або
Або
![]()
Краще давати числа не по порядку. Можна рахувати в межах 100. Кількість залежить від віку дітей, здібностей, програми.
Число 50 записується римськими цифрами як L, 100 - C.
Сильним дітям завдання ускладнюємо!
Диктант 76. «Як її назвати?»
На дошці й у зошитах методом графічного диктанту малюємо квадрат.
У зошиті від останнього списаного рядку спускаємося вниз на 2 клітини та відступаємо 2 клітини від лівого краю сторінки. Це місце позначаємо крапочкою. Від крапки вправо відраховуємо 8 клітинок і ставимо ще 1. Від першої крапки по вертикалі вниз відраховуємо 8 клітинок і ставимо третю крапку. Від другої вниз по вертикалі теж 8 клітинок. З’єднаємо 1 і 2, 3 і 4, 1 і 3, 2 і 4 крапки.
А тепер збоку від цієї геометричної фігури напишіть усі її назви, які ви знаєте.
 Це – плоска геометрична фігура, многокутник, чотирикутник, прямокутник, ромб, квадрат.
Це – плоска геометрична фігура, многокутник, чотирикутник, прямокутник, ромб, квадрат.
A B
![]() 4 см
4 см
C Д
Хто зможе всі назви прокоментувати, підібравши зведення правил, отримує 12 балів.
Додатково називаємо квадрат, враховуємо довжину його сторони двома способами (лінійкою і міркою 2 кл. = 1 см, а 8 кл. = см). Можна попросити сильних учнів ще й вирахувати S та Р квадрата й навести формули.
Диктант 77. «Парні – непарні»
(розподільний)
Учитель диктує (пише) на дошці (чи картці) числа, а учні розподіляють їх на парні – непарні у 2 рядки чи стовпчики. Можна просто підкреслити чи зафарбувати різним кольором. Хто зразу не зметикував – просто записує, а позначає потім. Назву диктанту бажано не повідомляти – хай учні самостійно визначать, за якою ознакою розподіляти за іншою ознакою, о потім додатково е визначте парні – непарні числа, позначивши їх певним знаком. Причому вчитель дає тільки підказку: над першим парним ставить зірочку, над непарним – крапочку тощо. Порівнявши числа, діти доходять до висновку, що числа ще можна розділити на групи: парні – непарні.
Диктант 78. «Круглі числа»
(вибірковий)
Учні отримують для опрацювання певну кількість чисел (їх диктують, пишуть на дошці, картці, у зошиті…). Вони на слух вибирають і записують (чи виписують, підкреслюють, зафарбовують, обводять) лише круглі числа.
Додатково можна попросити кожне число на 10 (5) і розташувати їх у певному порядку 9зростання чи зменшення) тощо.
Закріпляються «секрет», що кожне кругле число ділиться на 5 і 10.
Диктант 79. «Шифрувальники».
(«Видатні події, дати»)
Учням пропонують для диктанту розв’язати 3 – 5 прикладів і зафарбувати чи обвести числа-відповіді певним кольором. Якщо всі приклади розв’язані правильно, то з чисел-відповідей утвориться число-шифр.
![]() Наприклад:
Наприклад:
36 – 18 = 18
45 – 33 = 12
646 – 626 = 20 18 . 12 .2001 (року)
0 : 542 = 0
129 6 129 = 1
Учням пропонують записати числа-відповіді по порядку. Учитель ставить 2 крапки та підказує, що це число має відношення до одного з учнів класу. Воно позначає … (дату). Цього дня народилася наша Іринка і їй виповнюється … років. Так можна обіграти будь-яку дату й дізнатися, що вона позначає. Яка подія відбулася цього дня? Для підказки просто дописується після дати слово «рік», і тоді учні зорієнтуються швидше. Що ж було в цей день колись? День народження Іринки чи Тараса Шевченка, День Незалежності тощо.
Варіант А. Діти записують числа-відповіді в рядок через кому, а тоді позначають певним знаком потрібні числа:
76, 13, 10, 29, 14, 9, 45, 3, 18, 57, 14;
9.3.1814 року - ?
Варіант Б. Можна просто читати числа, що вийшли. Написати рядок відповідей:
36, 600, 748, 954, 7, 38, 45, 82, 116;
![]() 60 095 445 60 мільйонів 95 тисяч 445;
60 095 445 60 мільйонів 95 тисяч 445;
![]() 367 487 367 тисяч 487.
367 487 367 тисяч 487.
Варіант В. Можна запропонувати з чисел-відповідей скласти всі варіанти числа.
471 076, 104 776, 764 710,
477 610, 107 647, 761 047.
Усі числа прочитуються. Можна поділити ще й на розряди.
Диктант 80. «Магічне число»
Учитель пише на дошці певну кількість однакових цифр. За допомогою знаків і дужок учні складають приклади, використовуючи лише подані цифри.
Варіант А. Учні працюють з одним набором цифр або з різними.
Наприклад, з елементами «хвилинки каліграфії».
Учитель. Пригадайте, як пишеться цифра 3, і т. д.
- Написали. Допишіть ще 3 гарні трієчки. Прочитайте, яке число вийшло. Скільки в ньому розрядів?
З чотирьох трієчок складіть усі можливі приклади. Записувати можна лише знаки +, -, :, •, =.
Наприклад:
-
 3 333 3 • 3 = 3;
3 333 3 • 3 = 3;
-
 555 555 ?
555 555 ?
(55 – 5) : 5 – 5 = 5;
-
 44 444 444 ?
44 444 444 ?
(44 – 44) + 4 – 4 + 4 = 4;
-
 1 111 111 111 111 ?
1 111 111 111 111 ?
11 111 : 11 111 • 1 : 1 = 1 ;
-
 666 666 ?
666 666 ?
66 : 66 • 6 =6;
66 : 6 • 6 = 66;
(6 • 6) – (6 • 6) + 6 = 6;
-
 66 666 666 666 – 666 + 6 = 6;
66 666 666 666 – 666 + 6 = 6;
(66 – 6) : 6 •6 + 6 = 66.
Бонус тому, хто сам придумає аналогічні приклади.
Диктант 81. «Де чий будиночок?»
(розподільний)
За певною ознакою числа розселяють по будиночкам:
а) одно-, дво-, трицифрові;
б) чотири-, п’яти-, шестицифрові;
в) парні – непарні;
г) круглі – не круглі;
д) лише клас одиниць, клас тисяч і одиниць, клас мільйонів, тисяч і одиниць.
Будиночок можна потім використати для проектів «Моє місто», «Математичне містечко» тощо.
Диктант 82. 2За цілим знайди частину, за частиною від числа – ціле»
Учитель диктує завдання, а діти записують тільки відповідь або приклад повністю.
1/3 від 12,1/4 від 28. Запиши число, 1/2 якого дорівнює 6 тощо.
Можна додавати іменовані числа:
1/10 м = ?;
1/2 км = ?;
1/6 год = ?;
1/100 км = ?
Який шлях пройшов Іванко, якщо 2/6 шляху – це 300 м? Добре, коли вчитель дає зразок, а далі приклади чи завдання придумують самі діти, усвідомивши «секрет».
Диктант 83. «Десятки»
Учні записують 10 – 20 чисел під диктовку чи з дошки. Учитель пропонує позначити в них загальну кількість десятків або десятків певного класу:
![]()
![]()
![]()
![]()
![]()
![]()
![]() а) 1203, 7009, 842, 90, 605, 348 492, 7 807
а) 1203, 7009, 842, 90, 605, 348 492, 7 807
або
![]()
![]()
![]() 1203 709 548763
1203 709 548763
120 дес. 70 дес. 54 876 дес.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() б) 32 658, 900 732, 541 607, 869 451.
б) 32 658, 900 732, 541 607, 869 451.
У числі 32 658 маємо 5 десятків класу одиниць та 3 десятки класу тисяч.
Диктант 84. «Сотні»
Проводиться як різновид попереднього диктанту, але учні відмічають у числі кількість сотень.
Пізніше проводиться об’єднаний диктант «Десятки – сотні» або «Одиниці – десятки – сотні».
Наприклад ( - – одиниці, • – десятки, * – сотні):
3 648 954
-


 *•- *•-
*•- *•-
А далі аналіз числа за потребою.
Диктант 85. «Тисячі»
Визначаємо кількість тисяч у числі.
![]()
![]() 123 708 – 123 тисячі; 268 634 – 268 тис.
123 708 – 123 тисячі; 268 634 – 268 тис.
Буде добре, якщо вчитель відкриє дітям «секрет»: щоб підрахувати загальну кількість десятків у числі, треба закрити пальчиком 1 цифру справа й прочитати число десятків; сотні – 2 цифри, тисячі – 3 цифри, мільйони – 6 цифр справа.
3 647 891 – десятків 364 789;
3 647 891 – сотень 36 478;
3 647 891 – тисяч 3 647;
3 647 891 – мільйонів 3.
Усі числа прочитуємо чітко.
Диктант 86. «Математичний крос»
Сашко, Юрко та Мишко бігли крос. Сашко біг по першій доріжці, Юрко – по другій, а Мишко – по третій. Ти дізнаєшся, хто переміг, коли випишеш числа у відповідні колонки (доріжки).
Диктант складено таким чином, що доріжки-колонки нерівні. Кількість чисел до 30.

![]()
![]() а)
а)
![]()

![]()
![]()
![]()
![]()
![]() б)
б)
Кількість чисел 15 (вони є відповідями на 5 розв’язків прикладів кожного ряду):
1 ряд – 1 стовпчик (Сашко);
2 ряд – 2 стовпчик (Юрко);
3 ряд – 3 стовпчик (Мишко).
Після того, як учні вписали числа-відповіді в табличку (див. таблицю б), вони починають підраховувати, скільки метрів пробіг кожний хлопчик. Для цього складають оптимальним способом (усно) усі 5 чисел у рядку:
Сашко (39 + 71) + (54 + 86) + 102 = 342.
![]() 110 130
110 130
240
Сашко пробіг 342 метри і т. д. Потім порівнюємо результати й визначаємо переможця – І місце, ІІ та ІІІ місця.
Добірка прикладів – у межах програми. Слідкуємо. Щоб числа-відповіді легко складалися усно.
Диктант 87. «Цифра-невидимка»
На дошці (бажано магнітній) хаотично розташовані цифри. Учні закривають очі, а вчитель прибирає одну цифру. Саме її учні мають пригадати й записати в зошитах.
Варіант А. Замість прибраної цифри додають іншу, і учні записують цифру, що змінилося.
(Проводиться з шести річками під час вивчення і закріплення цифр.)
Варіант Б. Далі диктант ускладнюється. Записують пару цифр, що загубилася, і пропонують записати числа, які з них утворилися.
![]() Наприклад: 3, 7 37, 73.
Наприклад: 3, 7 37, 73.
Цифр може «пропасти» і 3 – 4 одразу.
Добре, коли учні знайдуть на дошці місце, де була цифра, і напишуть її там. Її тоді буде добре видно – решта ж цифр магнітні!
Диктант 88. «Судоку»
Встав у пусті клітинки цифри від 1 до 5 так, щоб у рядку,стовпчика вони не повторювалися.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 1) 1)
1) 1)

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2) 1)
2) 1)
Гру можна ускладнити: поле судоку звільнити, а дані (чорні) цифри діти вписують під диктовку вчителя.
1 ряд (зліва): третя клітинка 4, а четверта – 3.
2 ряд: перша клітинка зліва – 3, третя – 2, п’ята – 4.
3 ряд: у другій зліва – 4, у четвертій – 2.
4 ряд: перша зліва - , третя – 3, п’ята – 5.
5 ряд: перша зліва – 5, третя – 1, четверта – 4.
Диктують по стовпчиках або по рядках, діагоналях.
Додатково!
Додай (перемнож) числа:
1 стовпчик: 1 та 2 рядок;
2 стовпчик: 3 та 4 рядок;
3 стовпчик: помнож числа 5 рядка на 3 (4, 5, 6, 7).
Диктант 89. «Раціональний»
Запропоновані завдання учні розв’язують найбільш раціональним способом.
Завдання може бути й задача, що має кілька способів розв’язку. Завдань може бути 3 – 5. Учитель диктує приклади – учні записують.
Наприклад:
- 42 : 2 = 400 : 2 + 2 : 2 = 20 + 1 = 21;
- 39 + 64 = 40 + 64 – 1 = 104 – 1 = 103,
або
40 – 964 – 1) = 103;
- 27 • 4 = 20 • 4 + 7 •4 = 108;
- 1 м 14 см – 50 см = 100 см – 50 см + 14 см = 64 см;
- 13 • 5 + 7 • 5 = (13 + 7) • 5 = 100.
Диктант 90. «Усна контрольна робота»
Дібрати 3 – 7 завдань (відповідно до віку дітей та програми).
Наприклад.
- Розподіли (запиши, прочитай) числа.
- Розв’яжи приклади.
- Розв’яжи рівняння.
- Розв’яжи задачі.
-


 Вкажи, скільки ( , ) на малюнку.
Вкажи, скільки ( , ) на малюнку.
Усі завдання виконуються усно. Записуються лише відповіді.
Для зручності можна дати картку, куди вписуватимуться відповіді.
Завдання можна диференціювати.
Диктант 91. «Рахівнички» (округлення)
Підбираємо числа й округляємо до 10, 100, 1 000.
Учитель диктує 1-й стовпчик чисел і просить окрулити їх до 10, потім 2-й – до 100, 3-й – до 1 000. Можна одразу продиктувати число і сказати, що його слід округлити до 10, 100 чи 1 000.
Діти записують лише відповіді. Для зорового диктанту краще мати таблицю.
Закономірність: остання значима цифра < 5 – округляємо до меншого числа; якщо > 5 – до більшого, якщо дорівнює 5 – можна обрати будь-який варіант.
Наприклад:
число 236 округляємо до 10
6 > 5, значить буде = 240;
число 236 округляємо до 100
3 > 5, значить, округляємо до 200.
![]() Диктант 92. «Граф-схеми»
Диктант 92. «Граф-схеми»
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а) 640 : 16 • 12 + 90 : 19 • 15 • 2 : 18 : 25
а) 640 : 16 • 12 + 90 : 19 • 15 • 2 : 18 : 25
![]()
![]()
![]()
![]()
![]() Відповідь: 2.
Відповідь: 2.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() б) •5 : 2 • 7 + 350 • 100 – 3 000 – 1 – 50 000 :9 -111 : 4 ?
б) •5 : 2 • 7 + 350 • 100 – 3 000 – 1 – 50 000 :9 -111 : 4 ?
Відповідь: 250.
Диктант 93. «Мовчанка»

![]()
![]()
![]()
![]()
![]()
![]() Збільши на 1:
Збільши на 1:
![]()
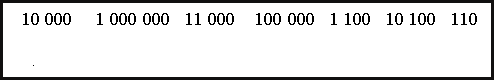
![]()
![]()
![]()
![]()
![]()
![]() Зменши на 1:
Зменши на 1:
![]()
Варіанти: збільши на 10, зменши на 10. Збільши в 10 разів, зменши в 10 разів тощо.
Числа добираються «хитрі», щоб був перехід через 10.
Діти мовчки беруть карку, виконують завдання і, піднявши картку догори, сигналізують, що завдання виконано.
Учитель може читати числа, а учень тільки записує відповіді в рядок через кому. Так важче! Числа вчитель добирає за складністю.
Диктант 94. «Математичні знаки»
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Варіант А. Учитель диктує, який знак треба написати, а учні вписують (можна працювати й за кртками).
Варіант А. Учитель диктує, який знак треба написати, а учні вписують (можна працювати й за кртками).
Варіант Б. Учитель диктує приклади або рівності – нерівності, учні вписують знаки або записують математичні дії і розв’язують приклади.
Диктант 95. «Математичні терміни».
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() Аналогічно до попереднього диктанту. Проводиться усно або за таблицею.
Аналогічно до попереднього диктанту. Проводиться усно або за таблицею.
Учитель заповнює ліву частину таблиці, а діти – праву.
Диктант 96. «Математичні закони»
На дошці, картці чи в зошиті даються приклади. Учні мають розв’язати їх і написати (сказати), яке правило чи математичний закон (властивість) застосовано.
![]() Даємо приклад:
Даємо приклад:
29 х 7 = 20 • 7 + 9 • 7 = 203.
Застосовано переставний закон множення та розподільний закон.
Формули:
a + b = b + a;
a • b = b • a;
(a + b) • c = ac + bc;
a + b + c = (c + a) + b;
c – (a + b) = c – a – b4
a : 1 = а;
а • 0 = 0;
1 • а = а
Тощо.
Готуємося до вивчення алгебри та геометрії.

![]()
![]()
![]()
![]()
![]() Диктант 97. «Продовжуй сам!»
Диктант 97. «Продовжуй сам!»
![]()
Можна таблицю не писати, а диктувати. Учитель – a + b й усно пояснюють, чому. Одразу ж можна записувати й приклад.
Учитель каже: a • b, діти пишуть b • a = 7 • 3 = 3 • 7. Варіантів є безліч!
Диктант 98. «Встанови відповідність»
Проводяться як математична розминка на початку уроку чи в кінці (під час виявлення рівня засвоєння знань учнями) в підсумковій частині уроку.
Дається таблиця, де вписуються в лівій колонці закони, а в правій – назви. Можна, щоб назву вписали самі діти. А також дописали формулу.
Варіант. Пишеться лише початок закону, щоб кінець дописали діти. Якщо обидві колонки заповнював учитель, то учні стрілочками з’єднують зміст і назви закону.
Диктант 99. «Цифромагія»
Полічи та встав літери в таблицю. Прочитай, що вийшло!
![]()
![]() Варіант А.
Варіант А.
![]()
![]() 124 • 4 = 496 308 • 2 = …
124 • 4 = 496 308 • 2 = …
![]()
![]() 247 • 2 = … 151 • 3 = …
247 • 2 = … 151 • 3 = …

![]()
![]()
![]()
![]()
![]()
![]()
![]() 236 • 2 = … 107 • 4 = …
236 • 2 = … 107 • 4 = …
![]()
Слово: «вересень».
![]()
![]() Варіант Б.
Варіант Б.
![]() 424 : 4 = … 846 : 2 = …
424 : 4 = … 846 : 2 = …

![]()
![]()
![]() 792 : 2 = …
792 : 2 = …
Слово: «ура».
Диктант можна використовувати на будь-якому етапі уроку. Приклади диктують чи пишуть, а от картка-дешифратор – обов’язок! Туди учні вписують слово-відповідь. Зашифрувати можна будь-що: тему уроку, назву твору, вид роботи.
Діти люблять, коли зі слів потім складається прислів’я, приказка, задача, коли утворюються пари синонімів, антонімів, одно корені слова. Завдання може послужити для планування інтегрованого уроку.
Можливості необмежені!
Диктант 100. «Помилковий»
Дається картка, де в кожному завданні є помилки. Їх треба знайти й виправити. Складніше це роботи, коли деякі приклади розв’язані правильно (але учням цього не говорять). Можна працювати й на дошці.
Завдання добирає вчитель за потребою. Регулює їх складність, зміст (тематику та кількість (обсяг)).
Додаток 2
У СВІТІ КАЗКОВОЇ ГРАМАТИКИ
Нестандартні дидактичні матеріали з української мови
Вступ
Може, хтось гадає, що граматика нудна?
Раджу вам цю книгу прочитати.
Спробуйте і впевнитесь: захоплива вона,
Весело граматику вивчати!
Хащами жахливих незліченних помилок
Стасик і Мишко колись блукали,
Доки не дісталися галявини казок.
О! Які сюрпризи їх чекали!
То був світ граматики, казкової, ось так!
І казок було там так багато!
Про слова та букви,про апостроф – дивний знак –
Усі вони відкрилися хлоп’ятам.
Стасик і Мишко запам’ятали ці казки
І тепер помилок не бояться.
Пишуть бездоганно ці чудові малюки,
На «відмінно» в школі вони вчаться.
Усі казки граматики, серйозні та смішні, –
Усі вони насамперед повчальні,
А до того ж всі вони – магічні, чарівні,
Бо допомагають у навчанні!
Казку прочитавши, дай відповідь чітку
На всі поставлені питання
І ретельно, якісно (ніяк не нашвидку!)
Виконати спробуйте завдання.
Розділ I. Граматичні казки, запитання і завдання до них
ДРУЖНІ НЕВИДИМКИ Є в Алфавіті будиночок звуків. Ось він.
Уважно розглянемо його. Праворуч, в окремій частині, мешкають голосні звуки: [ а, у, е, і, о, и] . Їх 6. Ліва частина – помешкання приголосних звуків. Перший поверх займають непарні приголосні. З них лише [ ф ] на половину глухий, а непарних сонорних аж 9. Зверху тверді, знизу м’які. Завжди м’який звук [ й ], як бачите, приставив драбинку до голосних і разом з ними утворив букви Я, Ю, Є, Ї, що не є звуками, і тому вони не в будиночку.
У верхній частині мешкають парні приголосні. Ліворуч – глухі. Праворуч – дзвінкі. Букву Щ теж не пускають до будиночка звуків, бо вона містить у собі два звуки: [ ш ] і [ ч ].
Гуляє на подвір’ї м’який знак. Адже він не позначає ніякого звука. Отже, і в будиночку звуків жити не може.
Горланить півень на даху голосних звуків. Вони ж голосні, співучі.
Дзвінкі приголосні утворюються за допомогою голосу й шуму, тому з ними дружить мишеня. Воно ж і голос подає, і шарудить. А глухі приголосні утворені лише шумом. Бачите: над ними дощик іде, шум є – а голосу нема.
Ось такий цікавий будиночок - музей звуків ми відвідали в Алфавіті.


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Запитання і завдання.
1. Скількі голосних звуків в українській мові?
2. Скільки парних дзвінких та глухих приголосних звуків? Назвіть їх попарно.
3. Які дзвінкі не мають парних глухих звуків?
4. Серед поданих слів знайдіть і назвіть лише ті, в яких усі приголосні звуки – дзвінкі: вітер, мідь, зима, ніжний, берег, дорога, смородина.
5. Серед переліку слів знайдіть і назвіть ті, в яких усі проголосні звуки м'які: сіль, неділя, тінь, Лілія, сяйво лінія, осінь, лютий.
6. Серед поданих слів знайдіть і назвіть ті, в яких звуків більше, ніж букв: щука, ячмінь, гедзь, надія, єнот.
7. Серед поданих знайдіть слова, в яких звуків менше, ніж букв: дзеркало, бджола, зелень, юність, яблунька.
М'ЯКИЙ ЗНАК ТА ЙОГО ДРУЗІ
Відростив собі животик
Знак м'який, м'який, як котик!
Знайте: буква ця німа,
В неї голосу нема!
Загадковий, хитрий знак!
Не читається ніяк!
І сам не вимовляється,
І букв багатьох цурається!
Та потрапивши до школи,
Він пом'якшує вимову,
Може слово геть змінити.
Отже, треба з ним дружити!
Хочеш приклад? То дивись:
"РИС", а знак допишеш – "РИСЬ"!
Все це знак м'який зробив:
З каші звіра утворив!
Знайте: буква ця німа
Лиш коли стоїть сама,
З приголосних поруч стане –
Звук м'який одразу стане:
![]() Мить [ т' ], міць [ ц' ], мазь [ з' ], сіль [ л' ], лось [ с' ], сядь [ д' ], гедзь
Мить [ т' ], міць [ ц' ], мазь [ з' ], сіль [ л' ], лось [ с' ], сядь [ д' ], гедзь
![]() [ дз' ], день [ н' ], трьох [ р' ].
[ дз' ], день [ н' ], трьох [ р' ].
Приголосні [ т' ], [ с' ], [ ц' ], [ д' ], [ л' ], [ р' ], [ дз' ], [ з' ], [ н' ].
Часто ходить з ним за руку,
Він пом'якшує ці звуки.
Іншу звуки з ним, повір,
Ворогують з давніх пір!
Тож м'якими не бувають,
Бо стосунків з ним не мают.
Є, щоправда, інші звуки,
Знака м'якшення онуки:
[ і ], [ й' ].
Право він таке дає
Буквам і, я, ю та є:
Як за приголосними стануть,
То також м'якими стануть.
Навіть звуки найтвердіші
Буква I пом'якшить враз:
Після Б ти І напишеш,
[ б' ] – пом'якшений у нас!
Все затямив? Молодец!
От і казочці кінець.
Запитання і завдання.
1. Для чого потрібна буква, котра не позначає жодного звука? Порівняй: син – синь; лан – лань.
2. Назвіть букви, що позначають приголосні звуки, після яких у словах української омви вживається м'який знак. Якими тоді стають ці звуки?
3. Які букви можуть позначити не м'які, а лише пом'якшені приголосні звуки?
4. З'єднайте слово й відповідну звукову модель:
НАГОЛОС-ЧАРІВНИК
Є значок маленький,
Йому Наголос ім'я.
Міцно з ним пов'язана
Вся голосних сім'я.
Наголос – наш друг
І дуже добрий помічник.
Наголос – відомий,
Славнозвісний чарівник.
"Замок", якщо схоче,
Перетворить на "замок".
Звук під ним чіткий,
Наприклад: килим – килимок.
Іноді він грається
Із нами залюбки,
Роблячи у слові чарівні свої стрибки.
Став над "о" – ворона,
Перескочив – ворона.
Це не птах – кобила,
Має чорну масть вона.
Якось перескочив
(Справжнє диво це було!) –
І прислівник "тепло"!
Став іменником "тепло"!
"Плакати – плакати".
Хто б без нього прочитав –
Це плакат чи плаче хтось?
А наголос постав –
Стануть зрозумілими
Одразу всі слова.
Сорок п'ять сорок –
З числа пташок зробив! Дива!
Наголос – відомий славнозвісний чарівник.
Наголос – наш друг і
Дуже добрий помічник.
Він вам допоможе залюбки у навчанні.
З ним вас подружитися потрібно, малюки!
Запитання і завдання.
1. Які чарівні перетворення можуть траплятися зі словами завдяки наголосу?
2. Складіть речення зі словами.
Замок – замок.
Дорога – дорога.
Мала – мал.
Кругом – кругом.
Води – води.
Плакати – плакати.
Брати – брати.
Тепло – тепло.
Гірка – гірка.
Ірис – ірис.
Лови – лови.
Ворона – ворона.
3. Напишіть диктант.
Наголос
Культура мовлення – це її правильність, точність, виразність. Дуже важливо рисою культури мовлення є правильний наголос у словах. Потрібно говорити так: завдання, читання, запитання, кілометр, сантиметр, центнер, столяр, одинадцять, чотирнадцять, випадок.
Завдання: позначити наголос у словах останнього речення.
ПІСЕННИЙ СПОСІБ
Коли закінчилось шосте Сергійкове літо і він пішов дор школи, його друзі трохи засумували. "Як же ми без Сергійка? – непокоївся песик Бублик. – Що ж нам робити, поки він у школі?" "А от що, – сказав півень Гога, – ми теж будемо вчитися! У нас теж буде школа. Сергійко розповідатиме нам, чого навчився в школі, а ми теж це будемо вчити!" Думка всім сподобалася.
Пройшло кілька днів, і "хвостаті учні" вже дещо знали. Наприклад, голосні звуки. Курка Ряба цілими днями повторювала: "Ко-ко-ко!" (це вона "о" вивчала), Бублик гавкав (на "а" налягав), півник Гога уподобав "у" і горланив "Ку-ку-рі-ку-у-у!", цап Коземир вивчав "е", постійно мекаючи та бекаючи. Навіть мишенятко Пік не відставало – пищало "пі-пі-пі", натякаючи, що звук "і" теж голосний.
Але сьогодні Сергійко повідомив, що в школі вивчали наголос. Навчилися виділяти в слові наголошений звук виявилося зовсім непросто. Спочатку всі помилялися, але згодом навчилися. Кожен робив це по-своєму. Кицька Марта, наприклад, вимовляючи наголошений голосний, відкриваючи ротик більше, ніж звичайно: «Молоко-о», і цей звук звучав у неї довше, ніж інші. Бублик просто «відбивав» наголос лапою або хвостом. От тільки цап Коземир ніяк не міг збагнути, як розпізнавати наголос. Уже й кури почали насміхатися над бідолашним Коземиром. А от півник Гога виявився справжнім другом. Він не насміхався, а спробував допомогти цапові, пояснити, як це робить він сам. Гога злетів на тин і заспівав: «Коземи-и-и-р!».
І це допомогло. Коземир раптом усвідомив, що наголошений голосний – «и» і що він співається довго, чітко, протяжно. Його ні з чим не сплутаєш!
«Спосіб куме-е-едній, але доте-е-епний!» – проспівав задоволений цап.
Тепер і він навчився розпізнавати в слові наголошений голосний звук і навіть склав про це віршик:
Щоб наголос у слові розпізнати,
Це слово треба просто проспівати,
І наголошений – чіткий, протяжний звук –
Проявить себе сам, без зайвих мук!
Запитання і завдання.
- Позначте наголос у поданих словах:
гроза, загроза, вітерець,
адреса, прапор, комірець,
автобус, ліжко, гуска,
журба, метро, мотузка.
2.Позначте наголос у поданих слова і перевірте за словником:
Сантиметр, завдання, олень, виразно, випадок, читання, навчання, кілометр, центнер, загадка, помилка, запитання.
3.З’єднайте слова з відповідною звуковою моделлю:
![]()
![]()
![]()
![]()
![]() Голос комар
Голос комар
![]()
![]()
![]()
![]()
![]() Пекар горох
Пекар горох
4.Які з поданих слів відповідають звуковим моделям?
![]()
![]()
![]()
![]()
![]()
![]() Дерево лисина
Дерево лисина
Молоко болото
![]()
![]()
![]()
![]()
![]()
![]() Солома висота
Солома висота
Малина чоботи
![]()
![]()
![]()
![]()
![]()
![]() Борода
Борода
5.Прочитайте, позначте наголос у виділених словах.
а) Сонце на дає тепло.
Без нього тепло б не було.
б) Сидить на березі комар і не знає:
На березі жаба на нього піджидає.
УЧЕНЬ АРТЕМОНА
Якось у лісовій школі Мальвіна вчила Буратіно ділити слова на склади.
- Скільки складів у слові «дуб»? – питає.
- Не знаю, – каже Буратіно.
Ех ти! Артемон – и той знає! Артемоне, скажи: дуб.
Артемон був собакою і тому сказав «гав».
- Бачиш, один склад! – говорить Мальвіна. – А тепер скажи: «дятел». Артемон каже: «гав-гав» (це по-собачому «дятел»).
- Бачиш, Буратіно, Артемон знає, що два склади, бо двічі почув голосний звук. А тепер скажи: «Мальвіна».
Артемон радісно замах хвостом і весело загавкав: «Гав-гав-гав!»
- Ясно! – сказав Буратіно. – Зрозумів! Тут три склади! Тепер я все знаю. Можу й сам будь-яке слово поділити на склади.
- Добре, я рада. Спробуй поділити на склади слово: Карабас-Барабас.
Буратіно трохи подумав і голосно загавкав: «гав-гав-гав, гав-гав-гав», це означає 3 і ще 3!
Мальвіна здивовано глянула на Буратіно, потім на Артемона й мовила:
- Правильно, але ж ти не собака, навіщо гавкати?
- Бо мене Артемон навчив! – вигукнув Буратіно.
А потім Буратіно всім розповідав, як він вчився в лісовій школі та який він розумний:
- Ключиком до знань нових я оволодів!
Скільки в слові голосних, стільки і складів!
Гав-гав-гав-гав! У слові «Буратіно» 4 склади.
Запитання і завдання.
1.Яке важливе правило засвоїв Буратіно?
2.Поділіть на склади подані слова:

![]()
 Вітер, олень, учень, малюк, бігаю, авіація,надія, озеро, малюють.
Вітер, олень, учень, малюк, бігаю, авіація,надія, озеро, малюють.
Зразок: мрі я ти.
ДВА ЗАКОНИ ДЛЯ ЗАКРИТИХ СКЛАДІВ
Якось слова вирішили переправитися через річку в невеличких човниках. Потрібно було поділитися на склади, оскільки до кожного човника міг сісти лише один склад.
Усім відомо, що склад утворюється голосним звуком: скільки в слові голосних, стільки і складів. Але ж у словах є ще й приголосні, що не зливаються з голосними. Розгубилися вони: до якого складу приєднатися? Деякі слова сперечатися почали. Особливо слова КНИЖКА й МИШКА. Склади їх ледве не розірвали! То один склад перетягує до себе приголосні Ж і Ш, то інший.
Почула суперечку цариця Граматика й видала указ:

 «Дзвінкі перед глухим завжди.
«Дзвінкі перед глухим завжди.
 Поділить слово на склади!»
Поділить слово на склади!»



 Суперечка одразу припинилася. Слово КНИЖКА сіло в човник ось так: книж ка (дзвінкий [ж] перед глухим [к], як велів закон, розділив це слово, приєднавши ж до першого складу). А слово МИШКА вмостилося в човник іншим чином: ось так: ми шка. Тут не було дзвінкого перед глухим, отже, розділилося воно на склади за загальним правилом: в українській мові склади переважно відкриті.
Суперечка одразу припинилася. Слово КНИЖКА сіло в човник ось так: книж ка (дзвінкий [ж] перед глухим [к], як велів закон, розділив це слово, приєднавши ж до першого складу). А слово МИШКА вмостилося в човник іншим чином: ось так: ми шка. Тут не було дзвінкого перед глухим, отже, розділилося воно на склади за загальним правилом: в українській мові склади переважно відкриті.
 Щойно вмостилася «книжка» й «мишка», аж тут знову почалася суперечка. Цього разу між словами «чорний» та «кислий».
Щойно вмостилася «книжка» й «мишка», аж тут знову почалася суперечка. Цього разу між словами «чорний» та «кислий».



 – ЧОР НИЙ! – наполягало слово ЧОРНИЙ, – тільки так! А ти ділися теж так: КИС ЛИЙ!
– ЧОР НИЙ! – наполягало слово ЧОРНИЙ, – тільки так! А ти ділися теж так: КИС ЛИЙ!
– Ні, я хочу розділитися на склади по-іншому, – не погоджувалося слово КИСЛИЙ. – Краще так: КИ СЛИЙ, ЧО РНИЙ!
Довелося цариці Граматиці видати ще один закон. Цей закон задовольнив обох учасників суперечки. І ти послухай цей закон:
«Запам’ятай одну з наук:
Закриє склад сонорний звук!»
А сонорні – це непарні дзвінкі, що позначаються такими буквами:
Л, М, Н, Р, Й.










 Вони тепер не сперечаються і завжди слухняно закривають склад: вій на, паль ма, пар та, рам ка.
Вони тепер не сперечаються і завжди слухняно закривають склад: вій на, паль ма, пар та, рам ка.
 Слова ЧОРНИЙ та КИСЛИЙ також розділилися за законом: ЧОР НИЙ і КИ СЛИЙ. Зробили вони це з великим задоволенням.
Слова ЧОРНИЙ та КИСЛИЙ також розділилися за законом: ЧОР НИЙ і КИ СЛИЙ. Зробили вони це з великим задоволенням.
Як добре все робити за законом, коли він ще й співпадає с твоїм бажаннями!
Запитання і завдання.
1.Яке загальне правило поділу слів на склади? Користуючись ним, поділи на склади слова:
Просто, риска, маска, тепло, гречка, кораблі, свічка, добре, баклажан, сонячний, відро, молочний, щасливий.
2.В яких двох випадках склади в середині слова закриті? Користуючись цими правилами, поділи на склади слова:
Різкий, паркан, військо, культурний, бузковий, перша, доріжка, дайте, ріжте, банка, верхівка, конкурс, трамвай, верба, пальці.
ЧАРІВНА ПАЛИЧКА ФЕЇ ВЕЛИКОЇ БУКВИ
Колись у місті Алфавіт усі букви були однакового зросту. Але якось у місті з’явилась прекрасна незнайомка – фея. У руці вона тримала тоненьку прозору паличку. О! То була не звичайна паличка – чарівна! Коли фея торкалась цією паличкою якоїсь букви, паличка починала світитись, а буква миттєво виростала.
– І до мене доторкнись! І до мене! – наперебій просили букви. І фея залюбки виконувала їх бажання.
– Ми будемо звати тебе фея Велика Буква! – задоволено сказав хтось, і всі букви почали аплодувати.
– Підлабузники! – пробурчав м’який знак – А я ніколи не погоджусь, щоб мене збільшили. Мені й так добре.
– І мені теж! – підтримала його буква И. – Ніколи не дам торкатися себе тією паличкою!
– Не хвилюйтесь, – сказала фея Велика Буква, – Я збільшуватиму вас лише тоді, коли ви будете стояти на початку речення!
– Дійсно, – засмутилася фея, – вам великими бути ні до чого.
А от решта букв, коли починають речення, з тих пір завжди стають великими.
Фея Велика Буква торкається своєю чарівною паличкою і тих букв, з яких починаються імена, по батькові, прізвища людей, клички тварин, географічні назви, назви планет, зірок, книг, журналів, кінофільмів тощо. Ці слова називаються власними назвами. А загальні назви пишуться звичайними маленькими буквами.
Але фея Велика Буква іноді робить дивовижні речі! Якось її чарівна паличка перетворила птаха орла на велике місто! А хлоп’ята-близнюки стали сузір’ям! Звичайні річкові риба та рак теж перетворилися на сузір’я, а хвостатий лев – на Лева Івановича!
Прекрасні почуття – віра, любов, надія – за допомогою чарівної палички стали не менш прекрасними жіночими іменами. Але найбільше здивувалися всі мешканці Алфавіту, коли фея Велика Буква торкнулася своєю паличкою до бублика з маком. Бублик раптом замахав хвостом і загавкав. Знаєте, чому? Бо він став песиком Бубликом! Ось така дивовижна паличка у феї Великої Букви! А без неї моя улюблена кицька Сніжинка, мабуть, давно б розтанула.
Запитання і завдання.
1.Коли вживається велика буква?
2.Складіть речення з поданими загальними назвами:
Лев, надія, терези, орел, земля, сонце, сніжок, буревій, барвінок.
3.Складіть речення з поданими власними назвами:
Лев, Надія, Терези, Земля, Сонце, Сніжок, Буревій, «Барвінок».
4.Поясніть вживання великої букви.
У виставі «Дванадцять місяців» Богдан грав роль Квітня.
Нашому Хвостику вже два роки, але він не кусається і на котів не гавкає.
5.Напишіть диктант.
Прекрасна й різноманітна природа України. Чудові краєвиди Карпат, дивовижна краса Кримських гір та Чорного моря нікого не залишить байдужим. А цього літа наша сім’я відпочивала на Десні. Там була й моя подруга Марійка з Полтави.
КАЗКА ПРО АПОСТРОФ
Апостроф в Алфавіті жив,
Із буквами завжди дружив,
Аж поки якось буква Я
Сказала: «Геть від нас!
Бо Алфавіт – це букв сім’я,
Нас 33 якраз!
А ти не буква, просто знак,
Ти нам чужий, не рідний, знай!»
Почув Апостроф ці слова –
Аж закрутилась голова.
Ніколи ще таких образ
Не чув він у житті.
Заплакав він, схопився враз –
І ось уже в путі.
Залишив місто Алфавіт.
«Піду, побачу білий світ».
Та що тут сталося! Хоч плач:
У малюків зник раптом м’яч,
Саме подвір’я зникло теж,
І м’ята, й бур’янець.
І на вечерю щось не те:
Без м’яса холодець!
А курка!? Бідолашний птах:
Немає пір’я! Просто жах!
Усі годинники стоять:
Дев’ятка зникла й цифра п’ять!
Із гаю зникли солов’ї,
А ще – реп’ях і в’яз.
В’юнів неначе хтось поїв,
Хлоп’ята зникли враз.
А у дівчат рум’янець зник…
Так жити Алфавіт не звик!
Усі кричать на букву Я:
«Тепер ми зовсім не сім’я!»
«Апостроф треба привести, –
Сказала буква М, –
Нам треба всім шукати йти,
Щоб не б не було проблем».
На пошуки гуртом пішли
І через день таки знайшли!
Усі зраділи, обнялись,
За руки міцно узялись:
І букви С, і І, і М,
Апостроф, буква Я.
І заспівали солов’ї,
Бо знов була сім’я!
У курки пір’я відросло.
Всім дуже весело було!
Запитання і завдання.
1.Які слова з апострофом згадані в казці? Запишіть їх.
2.Пограйте в «Словотворче колесо», складіть слова с апострофом:




![]()
![]()
3.Напишіть диктант.
а)Білий сніг покрив подвір’я.
Він м’якесенький, як пір’я.
б)Плакала м’ята:
– Погані хлоп’ята!
Кинули м’яч,
І тепер я зім’ята.
в) – Мар’янко, виполи бур’ян! –
Сказав онуці дід Дем’ян.
ПРІРВА МІЖ СЛОВАМИ
Є слова, як день і ніч, –
Прямо протилежні.
От я обачливий, скажім,
А ти – необережний.
Слова «великий» і «малий»,
«Сідати» і «вставати»,
«Холодний» – «теплий»,
«Добрий» – «злий»
Антонімами звати.
Про них вам казку розповім,
Її вам знати треба.
Є місто слів, і в місті тім
Будинок був – до неба!
В будинку мешкали слова,
Жили собі щасливо.
На кожнім поверсі – по два:
Недбалий і дбайливий,
А ще – веселий і сумний,
Гарячий і холодний,
Жили чистенький і брудний,
Та ситий і голодний.
Жили там правда і брехня,
Жили тривога й спокій.
Жили так дружно, як рідня,
А дім той був високий!
Аж якось вдарив з неба грім,
Земля аж застогнала!
І величезна прірва в ній
Слова ці роз’єднала.
Давно-давно це відбулось,
Та прірва є й донині.
Будинок навпіл розколовсь,
І в кожній половині
Тепер не дружно вже живуть
Слова оті – вороже.
Антонімами всі їх звуть
За зміст їх, геть несхожий!
Запитання і завдання.
1.Випишіть із казки антоніми, додайте ще кілька пар самостійно.
2.Знайдіть антоніми в прислів’ях.
Мир будує, а війна руйнує.
Краще з розумним загубити, ніж із дурнем знайти.
Повна бочка мовчить, а порожня гурчить.
Весна красна квітами, а осінь – плодами.
Гірко поробиш – солодко з’їси.
Вогонь – добрий слуга, але поганий хазяїн.
Хто горя не бачив, той і щастя не знає.
М’яко стеле, та твердо спати.
Ліпше своє мале, ніж чуже велике.
3. Доберіть антоніми до поданих слів:
Юнак – …
Щастя – …
Жорстокий – …
Весело – …
Підняти – …
Далеко – …
Вузький – …
Спекотно – …
Вечір – …
Осінь – …
Чистий – …
Заспокоїти – …
ПОБРАТИМИ
Ви, напевно, вважаєте, що тільки люди можуть бути друзями? А от і ні. Слова також уміють дружити. Дуже часто вони приходять одне одному на допомогу, можуть замінити собою інше слово так, що ніхто й не помітить заміни. Це тому, що значення деяких слів рівнозначне або таке схоже, що їх можна назвати побратимами! Хоч насправді схожі за значенням слова мають свою наукову назву – синоніми.
Одного разу в місті був концерт, виступав відомий музикант. Коли концерт закінчився, настав час аплодувати. Але слово «аплодисменти» десь забарилося, замешкалося. І тут на допомогу прийшло слово «оплески». Гучні, тривалі оплески виражали захоплення слухачів чудовою грою музиканта.
Ну й чим, скажіть, оплески гірші від аплодисментів? Звичайно, нічим не гірші. Вони – побратими!
Запитання і завдання.
1.Що таке синоніми? Доберіть до поданих слів рівнозначні:
Райдуга – …
Водограй – …
Абетка – …
Видатний – …
Хоробрий – …
Виднокіл – …
Дбати – …
Бентежно – …
Аероплан – …
Пілот – …
Вітрила – …
Журитися – …
2.Знайдіть серед поданих слів синоніми:
Лютий, дбайливий, несамовитий, злий, турботливий, упертий, наполегливий, завзятий, настирний, гнівний, схвильований, збуджений, збентежений.
3.Напишіть диктант.
Синонім
Як багато синонімів у нашій українській мові! Радуга й веселка, пестити й голубити, лагідний і ласкавий. А скільки їх у слова «метелиця»! Хуртовина, хурделиця, завірюха, віхола, завія, заметіль, хуга, хуговій, сніговерть – на всі смаки!
Синоніми прикрашають, збагачують мовлення.
ОКЛИЧКО
У Граматиці-країні
Мешкає Окличко-знак.
(Якщо хтось його не бачив
Виглядає він ось так: ! ).
Любить знак цей розмовляти
На підвищених тонах:
– Юрчику, не смій качатись
У багні в нових штанах!
Дуже часто він, злякавшись,
Верещить: «Рятуйте! Жах!»
І вигукує щоразу:
«Ой! Ой-ой!» чи «Ох!», чи «Ах!»
Дуже часто при звертанні
Подає він голос свій:
– Гей, хлоп’ята! Привіт, Сергійку!
Любий друже! Друже мій!
Знак цей дуже емоційний.
Як радіє, теж у крик:
– Я мастак! Я просто геній!
Я відкрив свій материк!
Із питальним знаком поруч
Враз суворим він стає:
– Хто це ллє у капці воду?!
– Хто розбив вікно моє?!
Поруч із питальним знаком
Ще й дивується цей знак:
– Та невже?! Невже я геній?!
Тож і справді я мастак?!
Іноді і так буває:
Краю радості нема!
Одного його замало –
Користуйтеся трьома: !!!
Ось такий у нас Окличко –
Дуже емоційний знак.
Користуйтеся ним, друзі!
Виглядає він ось так: !
Запитання і завдання.
1.Чи може знак оклику бути в кінці розповідного речення? Питального? Спонукального!
2.Знайдіть у казці окличні за інтонацією речення.
3.Прочитайте подані речення так, щоб вони стали окличними.
Мишко розв’язав задачу.
Ти скажеш мені правду?
Не сідай, тут пофарбовано.
4.Напишіть диктант.
Люблю весну
Я так люблю весну, люблю тепло,
Духмяний аромат пори цвітіння!
Здається, що ніяке в світі зло
Не пустить у цей час свого коріння.
Окрилена душа така легка!
А скільки в ній надій! А планів скільки!
І навіть грім бадьорить – не ляка,
І дощик не засмучує ніскільки!
ДОПИТЛИВІЙ ЧОМУЧКО
Всі ви бачили цей знак.
Виглядає він ось так: ?
Чомучко його звати,
Бо звик весь час питати.
«Чому? Навіщо? Як? Коли?» –
Щомиті тільки й чути!
«А що це значить – постоли?
А в постолах – це взутий!»
Такий допитливий значок –
Оцей «над крапкою гачок»!
Усе він хоче знати,
Тому і звик питати.
Запитання і завдання.
1.Які бувають види речень за метою висловлювання?
2.Виразно прочитайте вірш, дотримуючись питальної інтонації, де треба.
* * *
Чому,скажи, у кішки світять очі
У темряві, неначе ліхтарі?
Чому це сяють зорі серед ночі?
Чому вони зникають на зорі?
Ти і такі поставиш запитання:
Чому за літом осінь настає?
Чому туман буває на світанні?
Чому так б’ється серденько твоє?
І це твоє питання не останнє.
Я відповім на всі твої «чому»,
Хоч є і в мене також запитання,
Та ставить їх не знаю я кому.
3.Поставте потрібні знаки в кінці речення.
* * *
![]() Природи досконалість незбагненна (.)
Природи досконалість незбагненна (.)
Продумано все аж до дрібниць:
Світобудова, Сонячна система,
Життя – одна з найбільших таємниць,
Людина, здатна мислити й творити,
![]() Могутній мозок – це найбільше з див (.)
Могутній мозок – це найбільше з див (.)
Та неспроможний навіть він розкрити
![]() Секрет того, хто Всесвіт породив (.)
Секрет того, хто Всесвіт породив (.)
![]()
![]()
![]() Що є душа ? Яка вона ? Чи смертна (?)
Що є душа ? Яка вона ? Чи смертна (?)
![]()
![]() Чи вічний світ (?) У чому сенс буття (?)
Чи вічний світ (?) У чому сенс буття (?)
Чому резерви мозку незліченні,
![]() Коли така коротка мить – життя (?)
Коли така коротка мить – життя (?)
Це ж справжнє марнотратство – руйнувати
![]() Такий складний оцей Природи труд (!)
Такий складний оцей Природи труд (!)
![]()
![]() Чи є по смерті щось (?) Питань багато (.)
Чи є по смерті щось (?) Питань багато (.)
![]() Коріння всіх релігій саме тут (.)
Коріння всіх релігій саме тут (.)
СПОНУКАЛЬНИКИ
У місті Дієслів є вулиця Спонукальників. Мешкають на цій вулиці особливі дієслова: вони не мають часових форм і вживаються лише в спонукальних реченнях. Саме тому їх прозвали Спонукальниками.
Уже зранку на вулиці Спонукальників чути:
– Прокидайтеся!
– Починаймо ранкову гімнастику!
– Швидше вмивайтеся!
– Мийте руки!
– Давайте поснідаємо. А скуштуй-но млинці!
– Берімося до справ!
І так цілісінький день. То пропозиції, то накази, то прохання. Одним словом – спонукання. Навіть коти з цієї вулиці розмовляють між собою лише спонукальними реченнями! Послухаймо, про що так жваво говорить рудий кіт Воркіт, який щойно доїв рибину, і біла в рудих плямах Мурка, яка саме одержала від Оленки сосиску.
– Дай шматок сосиски, Мурко!
– А ти рибку подаруй!
– Ось бери хвоста від щуки!
– Сам хвоста того куштуй!
– Ну, не злись, давай дружити!
– На дурня не сподівайся!
Краще йди мишеня ловити!
– Скупердяйко, ну тримайся!
Воркіт кинувся віднімати в Мурки сосиску, але та швидко схопила її в зуби й подалася геть.
Спонукання спонуканнями, а на чужу сосиску навіть на вулиці Спонукальників зазіхати марно.
Запитання і завдання.
1.Що таке спонукання? Які знаки можуть бути в кінці спонукальних речень?
2.Знайдіть спонукальні речення в поданих віршах.
Чужа душа
Чужа душа – це темний ліс.
У неї й з ліхтарем не лізь.
Там ніч. Світанку не чекай,
Зірок у небі не шукай.
Там вічний морок, там пітьма.
Що схоче, висвітлить сама.
* * *
Попроси води
В чистої криниці,
В сонця весняного –
Променя ясного.
Попроси у вітру
Свіжого повітря,
У місяця блідого –
Щоб вказав дорогу.
Попроси в хмаринки
Дощика краплинку.
Тільки в серця злого
Не проси нічого.
Колискова дощу
Тихий дощ за вікном бубонить.
Він ласкавий такий, мелодійний.
Він співає про віру й надію,
Про любов, що у серці бринить.
Не стихай, не спиняйся, тривай.
Заколисуй збентежену душу.
Я забути про прикрощі мушу.
Тож співай колискову, співай!
Сну серпанком мене огорни.
Я вже чую м’який його дотик.
Відступають тривоги й турботи.
Не спиняйся, тривай, бубони.
ПРИБУЛЬЦІ
Колись у місті Слів жили слова, що складалися лише з кореня. Їх так і називали – корінні меш-канці.
Іноді в них відростали хвостики – закінчення.
Багато було корінних мешканців у місті Слів: хліб, вода, небо, море, вітер, ліс, ніч, день, вогонь, сад, сніг, дуб стіл… Та хіба всіх можна перелічити!
Корінні мешканці жили відособлено, кожен сам по собі, ні з ким не родичалися, але одного разу все змінилося. У місті з’явилися прибульці. Вони були різні: великі й маленькі, але всі такі кумедні! Частина прибульців називалася Префіксами. Були серед них роз і без, за, на, при, пре, прі, про, до, від, під, п, з і с та інші. А суфікси були ще кумедніші: еньк, оньк, есеньк, юсіньк, ісіньк, ищ, ель, ат, ят, ист, іст, к, ок, ик, ер, ор та ще багато-багато!
Прибульці звернулися до корінних мешканців з проханням:
– Дорогі, шановні Корені! Візьміть нас до себе, будь ласка! Ми вам станемо в пригоді! Це ми такі кумедні й незграбні, бо самі, а разом з вами ми утворимо сотню нових прекрасних слів, і у вас з’явиться багато родичів!
Тут суфікс чик пвідскочив до слова корінь, і всі побачили, що утворилося нове слово – корінчик!
До слова вода підбігли теж кілька суфіксів, і з’явилися водичка, водяний, водиця.
– Як цікаво! – сказало слово ліс – тепер у мене є родичі: лісок, лісник, лісовичок і навіть проліски!
– Ми згодні прийняти вас у нашу сім’ю, – сказало слово вітер, – адже тепер я буду не один. Он скільки родичів у мене: вітерець, вітрище, вітряк, вітрюган, вітряк, вітрила!
Навіть слово двері проскрипіло:
– І ми згодні, у нас тепер теж будуть родичі – дверцята.
Оскільки всі корінні мешканці погодилися прийняти прибульців, суфікси та префекси швидко взялися до роботи. Вони утворювали нові й нові слова.
Тепер у місті Слів кожен корінний мешканець маж родичів – спільнокореневі, або споріднені слова.
Запитання і завдання.
1.Подумайте, чи однакові суфікси в словах водиця і криниця, вербичка і сестричка, синочок і віночок.
2.Що спільного в словах кожушок, реп’яшок, горбок, голубок, черевичок, пушок?
3.Що спільного в словах розгорнув, розпишу, розбитий, розвідник, роздав, розкажу?

![]()
![]()
![]() 4.Знайдіть у тексті слова, що відповідають такій будові:
4.Знайдіть у тексті слова, що відповідають такій будові:
а) ;
![]()
![]()
![]()
![]() б) ;
б) ;
І знову з диво-пензлем ходить осінь,
Багряні фарби й жовті скрізь наносить –
Дерево золотить. Ще мить, ще трішки –
І золото покриє всі дорожки.
5.Напишіть диктант.
Суфікс
Українська мова дуже багата на суфікси. Вони відіграють велику роль у нашому мовленні. Які різні значення, яких неймовірних відтінків надають словам суфікси!
Голуб, голубок, голубчик, голуб’ятко,голубонько, голубці, голубити. Кіт, котик, котусь, котичок, котяра.
Суфікси збагачують мову, додають їй емоційного забарвлення.
Завдання: виділити суфікси в словах 2-го абзацу.
ЛИС І ЛИСИНА
Старий Лис Рудохвіст сидів на березі лісового озера. У дзеркальній воді він бачив своє відображення, яке зовсім не піднімало йому настрою. А тут іще й Сорока Скрекотуха своє «добре» слово вставила:
– У старого кума-Лиса голова вже зовсім лиса!
– Таки лиса…лиса?! Може, тому й лиса, що я Лис? – подумав Рудохвіст. І з цими думками пішов старий Лис до дійового професора Пугача Премудрого, щоб той пояснив йому, чи існує якийсь зв’язок між ним, Лисом, і оцією його лисиною.
Вислухавши Лиса, Пугач усміхнувся і промовив:
– Заспокойся, друже, не один ти лисину маєш, і в мене на потилиці пір’я повилазило! А слова «лис» і «лисий» справді дуже цікаві, тому що корені в них однакові (лис), але значення зовсім різне! Лисий, лисина, облисів – усі ці слова мають відношення до випадіння волосся. А до тебе, Лиса, мають відношення зовсім інші слова: лисиця, лисенята, лисяча (нора). Оце справжні твої спільнокореневі слова! А лисина нехай тебе не турбує!
– Дякую, професоре! – сказав Лис, – я все зрозумів. Справжні спільнокореневі слова мають не лише спільну буквенну частину, а й змістом пов’язані. А чи є інші такі слова, зі схожими і водночас несхожими коренями?
Пугач відповів:
– Звісно. Ось іще кілька прикладів таких слів. Подумай, які з них мають мають не тільки спільну буквенну частину:
Вода, водій, водичка водити;
Літо, літечко, літак, літати;
Радість, порода, радитись, зрадіти;
Гора, горить, горе, підгоріти.
Лиса лисяча голова, не дуже довго думаючи, знайшла справжні спільнокореневі слова. Сподіваюся, ваші дитячі голівки зроблять це ще швидше!
Запитання і завдання.
1.Які дві ознаки споріднених слів?
2.Чи є спорідненими виділені слова? Доберіть самостійно кілька споріднених.
Гусак, задравши в гору ніс,
Плотвичку з річки гусці ніс.
БЕШКЕТНИКИ Е ТА И
Звуки [е], [и], якщо вони в словах ненаголошені, звучать не дуже чітко, наближаючись один до одного, і їх навіть можна сплутати. А вони навмисно прикидаються один одним, щоб погратися з учнями! От і причина багатьох помилок. Так, для декого з учнів ця гра має погані наслідки…
Як добре, що існує спосіб розпізнати цих бешкетниківЙ Цей спосіб – перевірка наголосом! Адже, як сказано в одній знайомій пісенці:
«Наголос – відомий, славнозвісний чарівник!
Наголос – наш друг, помічник і рятівник!»
Він завжди приходить на допомогу, перевіряє сумнівні звуки і пояснює дітлахам:
– Ненаголошений и – е перевіряти треба.
Чому н…ебесний пишуть з е?
Бо е у слові небо!
Чому гр…бочок пишуть з и?
Тому що гриб, малята!
Потрібно звуки [е] та [и]
Завжди перевіряти!
Наголос – дійсно могутній чарівник і завжди допомагає перевіряти сумнівний [е] та [и] в словах, до яких можно підібрати перевірні. На жаль, існують слова, де й наголос безсильний. Але кожне – словником! Перевіривши раз, запам’ятайте написання. «Щоб раз по раз у словник не заглядати, треба свою пам’ять розвивати!» – завжди радить дітлахам добрий дядечко Словник.
II
Буква А дуже спостережлива й допитлива. Спостерігаючи за витівками бешкетників Е та И, вона помітила, що їх не завжди можна викрити за допомогою наголосу. Судіть самі.
Стирати, але стерти,
Завмерти, але завмирати,
Стеле, але вистеляти,
Збирати, але зберу.
Помітили, що відбулося чергування звуків [е] – [и]? Наголос тут нічого не вдіє. Буква А гордо заявила:
– Тепер А – ваша рятівниця!
Я теж, повірте, чарівниця!
На [и] завжди я вам вкажу,
Бо тільки з ним, не з [е] дружу!
Уважно погляньте: А дійсно завжди стоїть за коренем,, де буква И:
Стирати, завмирати, вистилати, збирати та в інших похідних словах.
У всіх цих словах [е] – випадний звук, тобто він випадає в похідних дієсловах: терти – тру, завмер – замру, беру – брав.
Тепер ви знаєте ще один метод викриття бешкетників [е] та [и] – метод букви А. Користуйтеся ним, коли маєте справу з дієсловами та словами, що походять від них.
Запитання і завдання.
1.Як перевірити ненаголошені [е] – [и] наголосом? Які ще є способи перевірки?
2.Користуючись «методом наголосу», перевірте слова та встав потрібні букви:
Тр…мати - …
Пол….вати - …
Стр…бати - …
Сп..котний - …
Опл…ски - …
Р…готати - …
В…сокий - …
Л…генький - …
(Слова для довідок: підтримати, лити, підстрибує, спека, плеск, регіт, вище, легко.)
3.Вставте пропущені букви. Поясніть свій вибір.
а) Сталеві два кр…ла
Н…если у вись орла.
Він швидкість наб…рав,
І обрій все зростав.
Він думав: в…сота –
Єдиний сенс ж…ття.
б) Споч…вають лози –
Ніби неж…ві,
І лягають роси
Спати на траві.
Клопіт і тр…воги
Задрімали теж.
Сплять лани й дороги.
Тишу не б…нтеж.
ЯК ЛИМОН ЛИМОННИМ СТАВ
У Граматиці-країні є дивовижне озеро, де народжуються слова. Перш ніж вийти на білий світ, слова плавають у цьому озері у вигляді окремих частинок. Іноді ці частинки, сподобавшись одна одній, з’єднуються в одне слово. Буває, що з озера виходять окремі слова, які складаються з багатьох частинок. Справжні ланцюжки! А найцікавіші – ті, що стискуються між собою двома однаковими буквами, утворюючи подвоєння на стиках. От про них і піде мова.
Плавав колись у тому озері корінь слова – ЛИМОН. Уже хотів виходити з води, як зробив один з його братиків-близнюків. А ще один братик-близнюк не спішив і дочекався, коли до нього причепився суфікс ЧИК.
Разом із цією частинкою ЛИМОН став словом ЛИМОНЧИК. «Може, і мені зачекати?» – щой но подумав третій близнюк, як до нього приєдналася маленька частинка – сефікс Н.
Таких частинок в озері Народження Слів багато, вони часто чіпляються до коренів.
«Що ж це за слово з мене вийшло?» – подумав ЛИМОН, вірніше тепер вже ЛИМОНН, – треба швидше відрощувати собі закінчення, бо так я з озера не вийду». І тут справді в нього відросло закінчення, ніби хвостик! Знаєте, що за слово вийшло з озера на берег? Так, прикметник! ЛИМОННИЙ чи ЛИМОННА, адже закінчення слова міняють, як рукавички.
Тепер зрозуміло, чому в деяких словах буває збіг однакових приголосних? А які ще слова утворилися так само, як слово ЛИМОННИЙ?
Знайдіть їх серед тих, що струнко вишикувались у цих рядках.
Беззубий, безталанний,
Безвинний,бездоганний,
Денний, сонний, телефонний,
Кінний, відданий, бетонний.
Запитання і завдання.
1.Назвіть слова, в яких утворилося подвоєння внаслідок збігу однакових приголосних на стику префіксу й кореня.
2.Назвіть слова, в яких утворилося подвоєння внаслудок збігу однакових приголосних на стику кореня і суфікса.
3.Вставте, де потрібно, букви:
Ран…ій, вечірн…ій, пісен…ий, без…ахисний, об…итий, роз…броєння, без…відповідальний, осін…ій, туман…ний, сумн…ий, закон…ик, замовн…ик.
ЯК ПОСВАРИЛИСЯ ПРЕФІКСИ З І С
Щойно префікси З і С народилися,
Як одразу ж таки й посварилися.
Вже забули й самі, чому так сталося,
Та насупились, повідверталися,
Між собою не спілкувалися,
Й помиритеся не намагалися.
Дні за днями пролітали.
Префікси дорослі стали.
Треба братись до роботи,
Адже є у всіх турботи.
Щоб зі справами розібратися,
Довелося таки спілкуватися.
– У нас є спільний інтерес:
Обом слід до коренів приставлятися,
Тож потрібно у них розібратися.
Які – твої, які – мої,
А то почнуться в нас бої!
Префікс З промовив радо:
– Завтра зберемо нараду,
І шляхом голосування
Вирішимо це питання.
По цьому префікс С пішов
Додому спочивати,
А З… не спати він пішов,
А букви підмовляти,
Щоб до нього усі приєдналися,
Щоб із префіксом С і не зналися!
![]()
![]()
![]()
![]() – Зі мною ви зможете в небо злетіти,
– Зі мною ви зможете в небо злетіти,
![]()
![]() Зі мною задумане можна здійснити!
Зі мною задумане можна здійснити!
З’єднуйтесь зі мною, – каже, –
Я здійсню бажання ваші!
Букви рано-вранці встали,
Всі за З й голосували.
Крім п’ятьох, які в ту ніч були в дорозі.
Оскільки вони їхали на возі,
То з префіксом З не спілкувалися,
А от місяцем-ріжечком милувалися.
І коли до місця дісталися,
То до префікса С приєдналися,
Бо дуже схожа букса С
На місяць, що світив з небес.
Тож префікс С лише з п’ятьма
З’єднатись може не дарма:
Хай друзів не багато буде,
Аби були хороші люди,
Порядні, вірні, незрадливі.
І префікс С цілком щасливий
Із цими друзями своїми.
Час познайомитися з ними:
К, П, Т, Ф, Х – ці п’ять
Біля С завжди стоять!
Запитання і завдання.
1.Коли вживається префікс с-? А коли вживається префікс з-?
2.Щоб легко запам’ятати п’ять приголосних, перед якими пишеться префікс с-, достатньо запам’ятати фразу: кафе «птах».
Користуючись цією порадою, вставте з або с:
…тискач, …падає, …чинити, …цементувати, не…проста, …платити, …сунути, …шити,…конструювати, …формований, …стурбований, …початку.
3.Напишіть диктант, складений з прислів’їв та приказок.
Спершу справа, а потім забава. На годину спізнишся, за рік не доженеш. Не почавши, не скінчиш. Правду не сховаєш. Умій сказати, умій і змовчати. Слово – не горобець, вилетить – не спіймаєш. Скривився, як середа на п’ятницю. Моя хата скраю. Два брехуни однієї правди не скажуть. З дурнем каші не звариш. Порожній посуд здаля звенить. Як маєш збрехати, краще мовчи. Слово до слова – зложиться мова.
ПРАВИЛА АПОСТРОФА
У країну граматичну,
Морфологічно-фонетичну,
Раз до Апострофа прийшла
У гості дівчинка мала.
«Я, – каже, – Леся. Мені треба
Мерщій дізнатися про тебе!
Ти хто?»
Апостроф каже: «Знак.
Пишуть між буквами, ось так ’».
«Завжди? Усюди?» – «Що ти?! Ні!» –
«То розкажи про це мені!».
І розповів цей знак про себе
Усе, що всім би знати треба:
«Запам’ятай: Я, Ю, Є, Ї –
Завжди супутники мої.
Атож! У кожному слівці
Зі мною поруч букви ці,
Лише вони за мною йдуть:
Сім’я, пір’їна, в’ється, п’ють.
Б, П, В, М, Ф – губні,
Ці букви завжди примені.
Я після них люблю стояти:
Б’є, п’ять, в’язати, верф’ю, м’ята.
Й до Р прихильність маю я:
Подвір’я, пір’ячко, бур’ян.
Звичайно, як потрібно їх
Роздільно вимовляти,
Інакше не потрібно там
Апострофу стояти!
Даремно й ти не став мене:
Зоря, морквяний, свято.
Вимова слова – головне,
А ще потрібно знати:
Крім Р, є приголосний збіг –
Я не потрібен після них.
Ще після префіксів стою,
Де також виділяю
Наступні Я, Є, Ї та Ю.
Свою я справу знаю!
З’явився, з’їхати, об’єм,
Під’їхати, з’юрбився.
От бачиш, як у цціх словах
Апостроф знадобився!
Коли на приголосний звук
Закінчується префікс,
Таким словам я вірний друг!» –
Сказав Апостроф Лесі.
Запитання і завдання.
1.Коли потрібно вживати апостроф? В яких випадках апостроф перед я, ю, є, ї не ставиться?
2.Вставте, де потрібно, апостроф.
Дев…ятсот, зв…язок, дух…мяний, тьм…яний, реп…ях, сузір…я, від…їзд, з…ясувати, риб…ячий, від…ємник, без…ядерний, перед…ювілейний.
3.Напишіть диктант.
а)Що то за ліхтарик там
У листі червоніе?
Це ж суничка солодко,
П’янко духмяніє!
б) Я п’ю медвяні аромати
Достиглих яблук, груш і м’яти.
в) Вийди серед ночі на подвір’я,
У зоряну безодню подивись.
Десь палає Лебедя сузір’я,
Ніби манить у небесну вись.
г) Не роз’єднає й океан
Серця, що з’єднані любов’ю.
4.Поміркуйте і поясніть, чому російське прізвище Водоп’янов пишеться українською з апострофом, а Фатьянов – з м’яким знаком.
ЗОЛОТІ ПРАВИЛА ПЕРЕНОСУ
В одній країні граматичній,
Морфологічно-фонетичній,
Жив Перенос – маленький знак,
Та неабиякий мастак!
Він був розумний і кмітливий
І знав закони особливі:
Міг переносити слова
З рядка в рядок
Ось так: трова.
Коли в рядку не поміщались,
Слова до Переноса мчались.
В негоду люту, у дощі,
І вдень, і вранці, і вночі:
– Будь ласка, любий Переносе,
Перенеси нас, друже! – просять.
І Перенос не відмовляв,
З рядка в рядок переправляв
Слова, ось так: ожи-на, лі-то,
Ве-селка, сон-це, зли-ва, ві-тер.
Але слова все йшли і йшли,
Вже черги у дворі були!
Щоб не спинялась переправа,
Він написав п’ять мудрих правил.
І мудрих, і таких простих –
Свої п’ять правил золотих!
Тепер в країні граматичній,
Морфологічно-фонетичній,
Їх знає навіть і маля,
Бо кожен бачить їх здаля.
І вам я раджу: прочитайте
І добре їх запам’ятайте.
П’ять правил Переноса
1.Для переносу слів завжди
Потрібен поділ на склади.
2.Як склад з одної букви лиш,
Не перенось його, облиш.
3.Передню букву, пам’ятай,
Від кореня не відривай!
4.Дж, дз також не розривають,
Як злиті звуки позначають.
5.Подвійний приголосний збіг –
Ти можеш розірвати їх.
У Переноса вільний час
З’явився еавіть, бо щораз,
Хто добре правила ці знає,
Тепер йому допомагає.
Чи є такі помічники
Між вас, шановні малюки?
Ось вам слова: завдання, косять,
Навчусь, ходжу, відзнака, осінь.
Які ж із правил золотих
Потрібні нам для слів отих?
Запитання і завдання.
1.Які існують правила переносу слів?
2.Як треба переноси ти слова:
Освіта, учень, прикраса, приклеїти, з’їхати, замріяний, тінню, кукурудза, навчаються, від’ємник?
ПРО ТИМКА І ЗАКОНИ ПРИЙМЕННИКІВ
У місті Слів мешкає дуже багато різних важливих слів зі значенням: іменники – назви предметів, прикметники – назви ознак, дієслова – назви дій та інші. Але серед мешканців міста Слів є й так звані службові слова; тобто слова без значення.
Одну з вулиць міста Слів – вулицю Прийменників – заселяють слова: за, на, над, по, про, до, для, без, через, від, під, біля, понад, поміж, з-за, з-під, при й багато інших.
Прийменники – слова службові, вони самі не відповідають ні на які питання і не можуть бути членами речення. Але це не значить, що прийменники не такі важливі, як інші слова. Важливі! От порівняйте: на столі і під столом. Є різниця? Є, і чимала! А все завдяки їм, прийменникам. Без прийменників не можуть обійтися ні іменники, ні прикметники, ні займенники, ні числівники. А от дієсловам прийменники не потрібні. Тому що жоден прийменник не стояв перед дієсловом! Такий у них закон.
Третьокласник Тимко ніколи не був у місті Слів, вулиці прийменників не бачив, з її мешканцями не знайомився і про їх закони, звісно, нічого не знав. Тому з ним трапилась незвичайна пригода. Писав він якось вправу:
Ранок тільки-но настав,
Качка з виводком – на став.
«Щось тут не те, – подумав Тимко, – так і є! Я знайшов помилку в підручнику! Адже всі прийменники треба писати окремо, і тут один раз окремо написано.Але ось тут помилка є!». І виправив:
«Ранок тільки-но на став».
Тут слова раптом ожили, і почалося таке! Слово «ранок» закричало:
– Ні на який став я не збираюся» На став повинні йти качка з виводком! А я настав, тобто, почався, прийшов. І прийменники тут ні до чого! Я ж дієслово, а тому перед дієсловом прийменників бути взагалі не може!
Тимко збентежено кліпав очина:
– Але ж прийменники зі словами пишуться окремо. Нам учителька говорила…
– Зі словами – так, – озвалося дієслово «настав», – але ж не можна писати окремо частинку слова. А ти відрубав від мене мою частинку і написав її окремо! «На» в мене повинно бути, бо це префікс, а ніякий не прийменник!
– Вибачте, – промовив Тимко, – тепер знатиму.
Не пиши вже чесне слово,
Прийменник перед дієсловом!
Закони ваші поважатиму
І краще правила вивчатиму!
Запитання і завдання.
1.Перед якою частиною мови не буває прийменників? На що іноді схожі прийменники? Як пишуться прийменники з різними частинами мови? А чому префікси не можуть бути написані окремо?
2.Запишіть, розкриваючи дужки.
Квочка всіх курчат (на) крила,
Бо закрапав дощ (на) на крила.
Був сюрприз для Лесі (в) ранці:
Хом’ячок сховався (в) ранці.
Пави сплять. Чрму (на) пав
Сон посеред дня (на) пав?
Ріже кум штани: «(На) шию
Цапу галстуків (на) шию!»
ДРУЗІ НАЗАВЖДИ
У Граматиці-країні жили собі Іменник та Прикметник, але ці поважні частини мови не були знайомі одна з одною. Та якось доля звела їх разом.
– Ти хто? – запитав Іменник, побачивши Прикметника.
– Я не можу відповісти на це питання, я знаю тільки який я? А ти який?
– А я можу відповісти лише на питання хто? Або що? А от який я? Не знаю…
Тут у кущах промайнув зайчисько. Іменник і Прикметник переглянулися.
– Заєць! – сказав Іменник.
– Сірий, довговухий, куцохвостий, прудкий! – додав Прикметник і посміхнувся.
Тим часом набігла хмарка і прямо Іменникові на ніс впала велика дощова крапля.
– Дощ, – промовив той.
– Теплий, літній,короткочасний, – заспокоїв Прикметник і засміявся, хоч на нього теж впало кілька крапель.
– Парасолька! – вигукнув Іменник, швидко розкривши її, і запросив нового знайомого сховатися від дощу.
– Гарна, яскрава! – похвалив парасольку Прикметник. Він був дуже радий зустрічі з Іменником, адже вони так легко порозумілися.
– Добрі, вірні, щирі, справжні…, – почав він схвильовано говорити. Іменник одразу зрозумів, про що той думає, і продовжив:
– Друзі! Побратими!
З того часу й почалася дружба Іменника й Прикметника. Прикметник так шанує Іменника, що зве його старшим братом і завжди стає на його сторону. Він навіть склав пісень про їх щиру дружбу й заспівав її Іменникові:
– Мені ти ніби брат,
Я надзвичайно рад
У всьому бути теж таким, як ти!
Твій рід, твоє число,
Відмінок твій візьму,
І поруч із тобою гордо я піду!
Іменник теж дуже шанує свого друга. А ще він надзвичайно любить відгадувати його загадки, тобто називати предмет за ознаками, які вказує Прикметник.
Хочеш погратися разом з ними?
Кислий, жовтий, соковитий, вітамінний… (лимон).
Білий, холодний, пухнастий, іскристий, морозний… (сніг).
Руда, пишно хвоста, швидконога, хитра, хижа… (лисиця).
Блакитне, чисте, безхмарне, прозоре, високе… (небо).
Запитання і завдання.
1.Який граматичний зв’язок існує між прикметником та іменником?
2.Вставте потрібні закінчення.
На висок… соснах; на вузьк… стежці; під розлог… вербою; дорог… подарунок; українськ… казок; близьк… другом; старш… синові; у глибок… криниці.
3.Доберіть до іменників прикметники з правого стовпчика:

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
СІМ БРАТІВ-ВІДМІНКІВ
Жили в країні граматичній,
Морфологічно-фонетичній,
Брати-відмінки. Називний
(Він був між ними головний)
Завжди предмети називав.
Про кожен з них хто? що? питав.
Ось так: це хто? – Їжак, лисиця.
Це що? – Машина, паляниця.
А це хто? – Дівчинка, школяр.
А це що? – Квітка, календар.
Відмінок другий – Родовий,
Був роботящий, діловий.
Всіх роду – племені питав,
Тому і назву цю дістав.
– Ти роду-племені якого?
Ніде не обійтись без нього!
Кого, чого, – питав, – немає?
Дороги, зайця чи трамвая?
Капусти, сала чи пшона?
Зозулі, півня чи зерна?
Давальний – щедрий був відмінок.
Кому? Чому? – усіх питав.
Ведмедю,бегемоту, півню,
Землі, повітрю – всім давав!
І ранку світлому, і ночі.
Давав і братові охоче.
Усе, що мав, усім давав.
Тому і назву цю дістав.
Знахідний брат четвертий звався.
Знайшов кульбабу й здивувався:
– Що я знайшов? Весну-красну!
А ще кого? Бджолу, осу,
Ведмедя, зайця і лисичку,
Знайшов метелика й синичку.
Орудний гордовито ходить,
Пишається. Скажи: ким? чим?
Собою, розумом, народом!
І ми пишатись будем ним,
Сім’єю, школою і містом,
Цукерками, ізюмом, тістом,
Коровою, котом, конем,
І ранком, і чудовим днем!
Місцевий вказує на місце.
На кому чи на чому? Де?
На морі, на землі, на річці,
У полі чи у лісі йде,
Мчить на машині, на коні,
У літаку або в човні,
В душі, у думці, уві сні,
А ще – в тобі він і в мені.
Відмінок сьомий зветься кличний.
Він дуже, дуже симпатичний!
Бо всіх так радісно гукає:
Веселко! Земле! Рідний краю!
Усіх він хоче привітати:
Бабусю, мамо, сестро, брате!
Відмінків сім, вони – брати,
Тепер знайомий з ними й ти.
Запитання і завдання.
1.Як розрізнити називний і знахідний відмінки? Як розрізнити давальний і місцевий відмінки?
2.Визначте відмінок кожного з іменників з тексту.
Життя лісу
У лісі й взимку не завмирає життя. На дубі в дуплі гризе горішки білочка. Ось на снігу видніються сліди лисиці. На пеньку відпочиває зайчик. І дятлові взимку є робота. Вмостився він стовбур сосни й видовбує комах.
3.Складіть речення з поданих слів, вживаючи їх у потрібних відмінках, додайте необхідні прийменники.
Машина, швидкість, мчала, велика.
Дороги, багато, автомобілі, автобуси, тролейбуси.
Оля, радість, подруга, допомогла, серветка, вишити.
Ліси, багато, дуби, сосни, берези.
4.Визначте відмінок іменників.
Стояв біля яблуні (…)
Посадив яблуні (…)
Сидить на яблуні (…)
Виросли яблуні (…)
Достигають груші (…)
Їсти груші (…)
Повісив на груші (…)
Злізти з груші (…)
5.Як відрізнити називний відмінок від знахідного й визначити підмет у реченні?
Вогонь розтопив лід.
Токар виточив гвинт.
Машиніст зупинив поїзд.
Місяць освітив сад.
Трактор оре поле.
СЕКРЕТИ РОДОВОГО ВІДМІНКА
У читальному залі школи № 11 сидів русявий школярик років 9-10 та гортав слова рик. Хлопчика звали Пізнайком, тому що він був дуже допитливим. От і тепер хлопчині не терпілося з’ясувати причину дивної «поведінки» іменників чоловічого роду однини в родовому відмінку. Чому дивної? А хіба не дивно, що такі схожі іменники, як, скажімо, гай і трамвай (адже в обох остання буква – й) у родовому відмінку вже мають різні закінчення: гаю, трамвая?!
– Я нарешті зрозумів! – вигукнув Пізнайко, – головне – це значення слова! З істотами все просто: у них завжди закінчення -а, -я, закінчень -у, -ю не буває, тож із ними проблем немає: чоловіка, ведмедя, сома, джмеля.
Труднощі викликають неістоти. Серед них є чітко окреслені предмети: різні одиничні предмети (олівець, трамвай, автобус, ключ, палець, ніс, пагорб, дуб, клен), які можна охопити оком; а також поняття, наукові терміни: квадрат, трикутники, кілограм, метр, літр, місяць, понеділок, жовтень, листопад, грудень, суфікс, відмінок тощо.
Ці іменники мають закінчення -а або -я! І словник це підтверджує: автомобіля, прямокутника, січня, вівторка, вареника, зуба, пирога, каштана, тюльпана, огірка, кореня, префікса, доданка.
– Молодець, хлопчику! Ти справжній дослідник! – почувся чийсь голос. Пізнайко зирнувся. Поруч стояв поважний пан у чорному капелюсі.
– Будьмо знайомі! Я – Родовий Відмінок. Ти зробив правильний висновок. Але це ще не все. Закінчення -а, -я мають ще й назви міст: Києва, Харкова, Львова, Парижа, Лондона, Севастополя, Рима. А їх поглядом не охопити, надто великі, чи не так?
– Так, – погодився Пізнайко, – а які закінчення мають назви країн?
– -У або -ю, – категорично промовив Родовий Відмінок. – Тільки так! Усе надто велике – великі території, споруди, як і всі нечітко окреслені предмети, збірні – мають закінчення -у, -ю. Можеш перевірити за словником: Дунаю, Бугу, Сибіру, Донбасу, Китаю, стадіону, піску, вітру, морозу, снігу, одягу, лісу, бузку…
– А чому «бузку»? Чим він відрізняється від «дуба»?
– Тим, що кущ. У кущів закінчення не ті, що в дерев! Запам’ятай: жасмину, агрусу, барбарису. А ще: маку, барвінку, хмелю, льону.
– Чому ж тоді «тюльпана»?
– Точно окреслений одиничний предмет! Адже ти можеш зірвати один тюльпан, один гладіолус. А от від хмелю, барбарису, моху хіба що відірвеш! – засміявся Родовий Відмінок.
– А чому «ранку», але «вечора»? – запитав Пізнайко. Але пан Родовий Відмінок зник. «Мабуть, виняток, – подумав Пізнайко й замислився. – Як багато таємниць у пана Родового Відмінка! Мабуть, ще не раз доведеться до словника звертатися».
Запитання і завдання.
1.Які закінчення мають іменники чоловічого роду, що позначають назви дерев? Міст? Наукових термінів? Назви окремих конкретних предметів?
2.Які закінчення мають іменники чоловічого роду, що позначають природні явища? Сипучі предмети? Річки? Точно не окреслені предмети й території.
3.Вставте потрібні закінчення (перевірте за словником):
Вийшов з га…, з будинк…, з магазин…, з лус…;
Біля автобус…, погреб…, каштан…, стадіон…;
Немає цукр…, вітр…, піск…, сніг…;
Повернуся з Сибір…, з Париж…, з концерт…, з вирі…;
Упав з дах…, з дуб…, з диван…, з балкон…;
Без почуття гумор…, без жал…, без страх…, без сором… ДИВНА СІМЕЄЧКА ПАНА ЗАЙМЕННИЧКА
Чи велика сімеєчка
В пана займенника?
Прямо скажу: не мала.
І дивну славу здобула.
Чому? Бо таки уже дивна: ніхто з цієї родини не називає речі своїми іменами. Тільки чути: ВІН, ТОЙ, ЦЕЙ, ТАКИЙ, ТУДИ, СЮДИ. А хто «він»? Який «такий»? Куди це «туди»? Про це можна тільки здогадуватися.
Ця кумедна родина мешкає в досить великому будинку, перший поверх займають лише так звані ОСОБЛИВІ ЗАЙМЕННИКИ. Їх теж чимало, тому праворуч і ліворуч від входу висять таблички. На тій, що ліворуч, написано:
Тут живе лиш однина:
Я, ТИ, ВІН, ВОНО, ВОНА.
А на другій:
Нерухомість множини.
Тут живуть МИ, ВИ, ВОНИ.
На кожній половин7і по три окремі кімнати, оскільки так званих осіб теж три. Кімната №1 ліворуч належить першій особі однини. Ця особа – Я, а праворуч кімнату №1 займає перша особа множини МИ.
Кімнати №2 ліворуч займає друга особа – ТИ, а праворуч – Ви. А кімната №3 належить третій особі. На половині однини там оселилися ВІН, ВОНА й ВОНО, а от праворуч мешкає тертя особа множини – ВОНИ.
Здається, усе просто. Але членів цієї сімейки впізнати іноді зовсім непросто! Вони здатні на всілякі вигадки. Іноді так зміняться, що й не впізнаєш! Скажімо, МЕНЕ де шукати? В якій кімнаті? А виявляється, що це третя особа однини – Я! Так разюче змінитися може й будь-яка інша особа: НАС, ТЕБЕ, ЙОГО, ВАМ, НИМИ.
Чи впізнаєш, хто з якої кімнати?
Запитання і завдання.
1.Назвіть особові займенники.
2.Знайдіть у тексті особові займенники, визначте особу, число, тва відмінки.
Гапка
Я пухнаста кицька Гапка.
Чорні в мене хвіст і лапки.
Є ще й смуги на мені.
Як у тигра – чарівні!
Зараз подруга Тетянка
Принесе мені сметанки.
Вона мене дуже любить,
Пригощає і голубить,
Навіть спить зі мною в ліжку.
Ще й якби ловила мишок…
3.Запишіть займенники в потрібній формі.
Спитав у (він).
Передав (він).
Глянув на (вона).
Люблю (вона).
Побачусь із (вони).
Зустріну (вони).
Заходьте до (ми).
Подарую (ви).
Дякую (ви).
Поговоримо з (ти).
Допомогти (ми).
Вдячний (ти).
КОМА ЗНАЄ СВОЄ МІСЦЕ
На конференції Розділових знаків виступила з доповіддю добродійка Кома:
– Познайомимось, я – Кома.
Усім я змалечку відома.
Кома – розділовий знак,
«Крапка з хвостиком», ось так!
Продемонструвавши всім свій хвостик, Кома продовжувала:
– Бачте, хвостичок маленький,
Коротенький, чепурненький.
А для чого я служу,
Зараз всім вам розкажу.
Дуже часто мне, діти,
Можна в реченні зустріти.
Я завжди перед а й але,
Це знає й дитинча мале!
Кома навела приклади (вона заздалегідь приготувала таблиці й тепер демонструвала на них своє місце).
![]()
![]()

– Коли є однорідні члени,
Ніяк не обійтись без мене.
Коли сполучників нема,
Стою я навіть між двома.


Сполучники зі мною в дружбі,
Бо на однаковій ми службі,
І часто в реченнях складних
Ми разом розділяєм їх.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Виділяю я звертання:

![]()
Знайти всі: під час читання
Теж важлива роль моя –
Вимагаю пауз я!
Чомучко Стасик був учасником конференції. Він дуже уважно вислухав цю доповідь, а потім запитав:
– Шановна Комо! Про звертання, однорідні члени речення без сполучників і навіть про складні речення я все розумію. Але чому в простому реченні перед сполучником і (або й) іноді кома є, а іноді немає?
– Відповім тобі, гаразд.
Коли і один лиш раз
В реченні простім буває,
Я стосунків з ним не маю.
А коли хоч два їх є,
Буде місце там моє!
Ці вже однорідні члени
Не обходяться без мене!
![]()

![]()
– Зрозумів, дякую за пояснення, шановна Комо, – сказав Стасик.
Кома, махнувши своїм коротким хвостиком, побігла назад у речення, поспіхом промовивши:
– Ще зустрінемось, малята!
Є ще випадків багато,
Де я теж значком служу.
Іншим разом розкажу!
Запитання і завдання.
1.Про які випадки вживання комі йшлося в казці?
2.Поставте коми, де вони потрібні, поясніть вживання.
Лінивий двічі робить… а скупий два рази платить.
Говорить прямо… але робить криво.
Підіймайте… свині… хвости… бо глибоко морем плисти.
Кулик невелик… а все-таки птиця.
Ото… мамо… хвалять нас: чи ви мене… чи я вас.
Запас біди не чинить… і їсти не просить.
Вміння… і труд все перетруть.
Ану вставай… чоловіче… третій півень кукуріче.
Праця годує… а лінь марнує.
Нащо й ліпший клад… коли в сім’ї лад.
ХАМЕЛЕОН-СПОЛУЧНИК ТА
Всім це правило відоме,
Знає й дитинча мале,
Що завжди потрібна кома
Перед А й перед Але.
А чи треба перед ТА?
Це проблема не проста!
Сполучник ТА мав звичку часто змінювати своє значення. Хамелеон, та й годі! Іноді прикидався мирним єднальним сполучником, і тоді він був так схожий на сполучник І! Як дві краплі води, їх не можна було розпізнати:
Ми збирали жолуді та шишки.
(Порівняй: Ми збирали жолуді і шишки.)
Правда ж немає різниці?
Але іноді сполучник ТА набував зовсім іншого значення. Він переходив у стан протиставних і ставав справжнім двійником сполучників А чи АЛЕ:
Ще тепло вдень, та ночі вже холодні.
(Порівняй: Ще тепло вдень, але ночі вже холодні.)
І знову – жодної різниці! У таких випадках перед ТА, як і перед АЛЕ, необхідна кома. Це створювало незручності, викликало певні проблеми в Катрусі:
– От капосний «хамелеон»! – скаржилася вона на сполучник ТА. – Завжди через нього роблю помилки!
І тоді сполучник І та Але вирішили допомогти Катрусі: один із них завжди з’являвся на місці хамелеона ТА, щоб Катруся могла побачити справжнє обличчя цього пустуна.
Тепер Катруся чітко знає:
Як рис АЛЕ ТА набуває,
Потрібна кома перед ним,
Оцим сполучником складним.
А коли схожий він на І,
Потрібна кома? Звісно, ні!
Запитання і завдання.
1.В якому випадку перед сполучником ТА потрібно ставити кому? Як можна за допомогою сполучників І та АЛЕ швидко розпізнати значення сполучника ТА?
2.Замініть сполучник ТА сполучником І або АЛЕ. Де необхідно, постав кому.
Слово – не стріла та (…) глибоко ранить.
Риба та (…) зайці заводять у старці.
Їж борщ з грибами та (…) держи язик за зубами.
М’яко стеле та (…) твердо спати.
Гарно пише та (…) брехнею дише.
Вовк линяє та (…) вдачі не міняє.
Тільки гав ловить та (…) витрішки продає.
ДОБРІ ГОЛОСНІ
Усі відомо, що існують парні глухі та дзвінкі приголосні. Вони дуже схожі за звучанням, і тому Дем’янко завжди їх плутає. Завтра контрольний диктант… Невже знову через оті капосні парні приголосні Маринка глузуватиме: «Це ж Дем’янко-помилянко! Він же без помилок і дня не проживе!»? Їй добре насміхатися, вона відмінниця, а Дем’янкові зовсім не до сміху.
Раптом тоненький голосочок пропищав:
– Не сумуй, Дем’янко, ми тобі допоможемо.
– Хто це? – здивувався хлопчик.
– Це ми, голосні! Ти нас не бачиш, бо ми звуки, а значить, невидимки. Але це не біда, головне, що ти нас чуєш.
– Вас то я чую, а от пані глухі та дзвінкі…
– А завдяки нам і їх теж почуєш! Не хвилюйся, усе буде гаразд!
Наступного дня, коли Дем’янко сів за парту, знайомий тоненький голосок підбадьорив його:
– Привіт, друже! Ми з тобою!
Тим часом почався диктант. Коли вчителька продиктувала слово «просьба», Дем’янко засумнівався, що писати – «з» чи «с». «Напевно, треба «з», так, здається», – невпевнено подумав він і вже хотів писати. Але тут, прямо біля вуха, тоненький голосочок промовив: «Просити!» Звук «с» у цьому слові прозвучав так чітко, так ясно, що Дем’янко більше не сумнівався і написав «просьба».
Добрі голосні ще кілька разів приходили хлопчикові на допомогу. Вони підказували, як перевірити й чітко почути сумнівний приголосний. Адже перед голосним будь-який приголосний звучить чітко!
Цього разу Маринці насміхатися не довелося, адже оцінку за диктант вона отримала таку, як і Дем’янко. Вірніше, Дем’янко – таку, як Маринка, бо це в неї завжди були відмінні оцінки.
Дем’янко повертався додому задоволений і всю дорогу насвистував і приспівував:
«Коли сумнівний парний звук
У слові зустрічається,
Він швидко і без зайвих мук
Тепер перевіряється:
Покличу хутко голосний –
Сумнівний стане враз ясний!»
Добрі маленькі чарівники-невидимки й тобі допоможуть. Поклич їх, коли засумніваєшся!
Запитання і завдання.
1.Як за допомогою голосних перевірити парні глухі чи дзвінкі приголосні, які вимовляються не дуже чітко?
2.Підберіть перевірні слова та встав букву:
Кі (г, х) ті –
Ні (г, х) ті –
Боро (т, д) ьба –
Дьо (г, х) тем –
Во (г, х) ким –
Ле (г, х) кий –
Моло (т, д) ьба –
Допомо (г, х) ти –
3.Прочитайте слова, чітко вимовляючи парні дзвінкі приголосні, як вимагає літературна вимова (дзвінко):
Дужки, загадка, везти, грядка, казка, шубка, бігти, грубка, скибка, бризки.
ЧАСТКА НЕ В МІСТІ ДІЄСЛІВ
У Граматиці-країні,
В славнім місті Дієслів,
Легендарним і гостиннім,
Частку НЕ хтось поселив.
Частка НЕ з дієсловами
Подружитись не могла.
–Я не стану поруч з вами,
Хоч би де я не була!
Не люблю вас! Не чекайте,
Я руки вам не подам!
І мене ви не гукайте,
Я не стану другом вам! –
І стоїть окремо НЕ.
– Не торкайтеся до мене!
Не чіпайте! Не підходьте!
Не турбуйте частку НЕ!
Та одній же нудно жити,
Всім це ясно і без слів.
Треба з кимось і дружити,
Як ти в місті Дієслів!
«Ненавидіти» – це слово
Полюбила частка НЕ,
І тому це дієслово
Не вживається без НЕ.
Пишуть «нехтувати» разом
(З ним у НЕ – любов сама!)
І «неволити», всяк знає:
Слова «волити» нема!
І «нездужати», «незчутись»,
«Непокоїтися» теж
Пишуть разом
(НЕ в них префікс),
Тут за смислом слова стеж!
Дружить НЕ й з дієсловами,
Що на НЕДО- почались.
«Недочути», «Недоспати» –
Дії, що не відбулись
В повній мірі, лиш частково –
Разом пишуть, пам’ятай.
Тож обдумуй кожне слово
І словник частіш гортай!
Запитання і завдання.
1.Чому з дієсловами нехтувати, ненавидіти, неволити, непритомніти, нездужатися, непокоїтися НЕ пишеться разом, а не окремо.
2.Напишіть дієслова з НЕ, розкриваючи дужки.
Яблунька
Ніби хижий беркут на зайчисько,
Налетів страшний буревій.
Перед ним верба схилилась низько,
До землі пригнувся деревій.
А хоробра яблунька (не) гнулась.
«Похилися!» – вітер їй велів.
«(Не) схилюся, – гордо усміхнулась, –
Хоч коріння вирви із землі!»
Вітер обійняв її щосили.
Тріснуло відламане гілля.
Та й тоді пощади (не) просила,
Тільки листом вкрилася земля.
3.Напишіть диктант, складений із прислів’їв.
Чого Івась не навчиться, того й Іван не знатиме.
Хто розуму не має, тому й коваль не вкує.
Не побігаєш – не пообідаєш.
Доки не впріти, доти не вміти.
Згаяного часу й конем не доженеш.
Правда суду не боїться.
Не кажи «гоп», доки не перескочиш.
Одрізаного не приставиш.
Ложкою моря не вичерпаєш.
УСІ ВАЖЛИВІ!
Усім відомо, що є самостійні частини мови та службові. Самостійні щось означають, на різні питання відповідають, тобто вважають себе цілком поважними особами. Ну й нехай собі вважають, не про них мова зараз! Мова піде про службові частини мови.
Зібралися якось вони всі разом і почали вихвалятися, які вони важливі.
– Без нас, вигуків, я взагалі собі життя не уявляю! Якби я вранці не крикнув «Ой!», ніхто б і не побачив, що вогонь спалахнув, – сказав вигук «Ой!». Йому почали аплодувати вигуки «Ох!», «Гей!», «Ех!» та інші.
Скоро почалася суперечка. Особливо наполягали на своїй важливості сполучники.
– Звичайно, ми найважливіші! – сказав сполучник І, – тут і думати нічого! Ми з’єднуємо і слова, і навіть окремі думки! Без нас не могло б існувати багатьох складних речень!
– Так, авжеж! – підтримали його сполучники БО, АЛЕ, А, ЯК, ЩОБ, КОЛИ та інші, – ми з’єднуємо слова й думки, неначе ланцюжки, нас треба визнати найголовнішими серед службових слів і призначити президентами нашої спільноти!
Частки скромно мовчали, хоча глибоко в душі вважали, що й вони могли б стати цілком пристойними президентами. Одна лиш частка НЕ сказала вголос:
– Я так не вважаю! Не погоджуюся, не визнаю!
Тоді частка ЖЕ, БИ, ОСЬ та ще кілька почали гомоніти:
– Це ж неподобство! Казна-що! Вам би треба було бути скромнішими, ось!
Прикметники теж ледве стримувалися від хвилювання.
– Це ж без нас не було б речень! Ні складних, ні простих! – закричав прийменник БЕЗ. Його підтримали інші. Прийменники ДО, ВІД, У, НА, ПІД, НАД навіть стиснули свої кулачки й хотіли кинутися на сполучники, але, на щастя, до бійки не дійшло, бо цариця Граматика, як завжди, з’явилася вчасно і сказала:
– Шановні, шановні службові слова!
У мене від крику болить голова.
Не треба війни, суперечок, прошу!
Усі ви важливі, це я вам кажу!
І далі нести вам важливу цю службу,
Тому я – за всіх вас! За мир і за дружбу!
Серед службових слів немає президентів. Вони ні від кого не залежать, але всі дружно й старанно виконують свої обов’язки, роблячи нашу мову такою чудовою!
Запитання і завдання.
1.Про які службові слова ви дізналися в казці?
2.Підкресліть прийменники однією рискою, а сполучники – двома.
Тихий дощ за вікном бубонить.
Українська пісня, і сумна, й весела, лине над Полісся, степом з полонин.
Фольклор із глибини віків несе цікаві й мудрі судження про все.
Цвіли первоцвіти, веселі, як діти.
З калини і квітів сплету я віночок.
Туга в серці бринить,і дощем бубонить сиротливо осінь.
ЧИСЛІВНИК
Частина мови ділова.
Числівник добре знає,
Що як від трьох відняти два,
Завжди один буває.
Він знає, що чотири й шість –
Це десять. І не тільки!
На всі питання відповість,
Якщо спитаєш «скільки?»!
Числівників, як тих зірок,
Багато-пребагато,
Бо безліч чисел, адже всі
І не порахувати!
Завдання.
1.Запишіть числа словами.
Розумна пташка
Зозуля зранку вже кує
І лічить все, що в лісі є:
64 клени,
7 ялин вічнозелених,
Сосен 180.
Та берізок 50,
3 дуби, 2 горобини,
22 кущі ожини,
![]()
![]() Мухомора 1 1 (півтора)
Мухомора 1 1 (півтора)
Й печериця ще стара.
3 вовки, зайців 16,
9 білок, змій 12,
901 мурашка
Й лиш 1 розумна пташка!
2.Провідміняйте:
Троє поросят, сім гномів, одинадцять братів.
ВІЙНА З ПОМИЛКАМИ
Завдання.
2.Напишіть диктант, перевірте себе та виконайте роботу над помилками: визначте тип орфограми, пригадай правило, виправте помилки.
Осінь
Після душного літа настала золота осінь. По узліссям ще ростуть гриби. На старих пеньках туляться один до одного опеньки. На дні лісового струмочка видно кожен камінчик. У прозорому небі пливуть хмарки. Ясної тихої днини літає над землею павутина.
Їжак
Восени в їжаків мало харчу. Поховалися в землю черв’яки. Зникли прудкі ящірки. Важко знаходити жуків і жаб.
Цілий день працює їжачок. Він ладнає собі тепле зимів’я, тягне сухе листя, мох. Стеле зимову постіль. Тепло буде взимку їжачкові спати.
Золота осінь
Стояла тепла ясна осінь. Осіннє повітря було прозоре, тихе. Велике золоте сонце пливло на захід. Під його косим промінням золотом сяяло жовте листя лип та беріз. З кожнім днем усе більше стає жовтого листя. Скоро осінній вітер зірве й це останнє вбрання, встеле подвір’я м’яким різнобарвним килимом.
Хліб
Хлібом годує тебе Батьківщина. Куди не закине життя – пам’ятай про хліб. Треба бути терплячим і мужнім у праці.
Батьки дали тобі перший хліб. Твій обов’язок – дати їм останній.
З дитинства треба бачити в хлібові живу душу рідної землі, сонця і неба.
Багато людей віддають хлібові все своє життя. Цінуй їхню працю! Шануй хліб!
Святиня
Шануй і поважай матір і батька. Вони дали тобі життя. Ти будеш дорослою людиною, але для матері й батька до останнього їхнього подиху залишишся дитям.
Вони ночей не спали біля твоєї колиски, коли ти хворів. Вони прислухалися до твого дихання, до биття твого серця. Пам’ятай завжди про це. Дорожи честю сім’ї, оберігай її, як святиню. Де б ти не був, ніколи не забувай про свою ріду домівку.
Каштани
Чарівні київські каштани навесні. Лопаються набубнявілі бруньки, і відбувається диво. Кожна перетворюється на рожево-білу квітку. Крони дерев, вкриті пишними суцвіттями, поширюють довкола ніжний запах, котрий віщує наближення літа.
Минає святковий травень, зів’ялі пелюстки запорошують асфальт. На каштанах з’являється зав’язь. Каштани – окраса нашого міста. Без них не можна уявити собі Києва.
Лісова красуня
Береза – справжня лісова красуня. Струнка, білокора, ніжна, вона прекрасня в усі пори року.
Навесні її довге гілля прикрашають зелені сережки. У вересні пишна, кучерява зелена крона починає жовтіти. Восени берізка розкішна, схожа на золотокосу казкову принцесу. І навіть взимку, коли зронить останнє своє вбрання, запорошена сріблястим інеєм, уся білосніжна, неначе в білім мереживі, береза прекрасна.
2.Перевірте своє вміння писати переклади.
Зозуленька
Якось мисливець помітив на узліссі дивного птаха. Він нерухомо сидів на сучку. Птах цей був досить великий, з кошлатим пір’ячком. Біля нього метушилися дві маленьки пташки. Одна підлетіла з черв’ячком у дзьобі й сунула його в рот дивному пташеняті.
Тут мисливець здогадався, що це було зозуленятко зі своїми названими батьками.
План
1.Кого помітив на узліссі мисливець?
2.Який вигляд мав птах?
3.Що робили маленькі пташки?
4.Про що здогадався мисливець?
Хитра білка
Оля та Галя пішли в ліс по горіхи. Нарвали дівчатка повний кошик. Повісили його на сучок великого дуба, а самі побігли рвати лісові дзвіночки.
На дубі в дуплі жила білочка. Побачила вона кошик з горіхами й почала носити горішки до свого дупла. Усі перенесла.
Повернулися дівчатка й дуже здивувалися: кошик був порожній. Довго не могли вони зрозуміти, куди зникли горішки. Раптом з дуба посипалися шкаралупки. То білка гризла горіхи. Тут дівчатка й зрозуміли, що трапилося.
План
1.Де повісили кошик дівчата?
2.Що зробила білочка?
3.Як дівчатка все зрозуміли?
Мурашки-ласуни
У горщик з медом забралися мурашки. Господар їх вигнав, обв’язав горщик мотузкою і підвісив його за гачок до стелі.
Одна мурашка залишилася в горщику. Наїлась вона й хотіла вийти. Довго бігала, доки дісталася до мотузки. Потім полізла на стелю і по стіні спустилася на підлогу.
Минув деякий час. І ось господар на мотузці величезну кількість мурашок.
Горщик був майже порожній.
План
1.Як господар заховав мед від мурашок?
2.Як мурашка вибралася з горщика й дісталася додому?
3.Що трапилося потім із медом?
Мати-ворона
Одного разу бабуся знайшла на вулиці поранену ворону. Вона принесла її до хати і поклала в ящик із курчатами. Вранці пішла подивится на курчат. У куточку сиділа ворона. Під її кри лами примостилося п’ять курчат. Двоє сиділо в неї на спині.
За кілька днів крило у ворони загоїлося. Бабуся її випустила. Але ворона кружляла навколо хати й кричала. У хаті пищали курчата. Бабуся випустила їх на подвір’я. Як зраділа ворона! Злетіла до них, розставила крила й голосно каркнула.
Так і лишилася ворона жити в бабусі.
План
1.Куди поклала бабуся ворону?
2.Що побачила бабуся вранці?
3.Що трапилося за кілька днів?
Розділ II. «Казкові» вправи
«КЛЮЧОВІ» ЗАВДАННЯ
![]()
![]() Символ «ключ» означає: перевір себе. Якщо завдання виконано
Символ «ключ» означає: перевір себе. Якщо завдання виконано
![]()
правильно, певні букви виписаних слів складуть назву казки або ім’я казкового персонажа.
1.Випиши слова, в яких потрібно вставити апостроф.
![]() Під…йом, кав…ярня, св…ято, ар…єгард, порт…єра, з…йомка, роз…яснення, Лук…янівка, сім…я, обов…язок, моркв…яний, нап…ються.
Під…йом, кав…ярня, св…ято, ар…єгард, порт…єра, з…йомка, роз…яснення, Лук…янівка, сім…я, обов…язок, моркв…яний, нап…ються.
![]() Перші букви слів складуть ім’я казкового персонажа.
Перші букви слів складуть ім’я казкового персонажа.
![]()
2.Випиши слова спочатку з пропущеною буквою и, а потім – з е.
![]()
![]() Т…рпіння, нах…лився, см…тана, тр…вога, кол…ктив, ст….хають,
Т…рпіння, нах…лився, см…тана, тр…вога, кол…ктив, ст….хають,
Інж…нер.
![]() Другі букви слів складуть ім’я казкового персонажа.
Другі букви слів складуть ім’я казкового персонажа.
3.Випиши тільки іменники.
![]()
![]() Прямо, брама, ікра, грає, літр, овал, позаду, споруда, ножі, іній, дай,
Прямо, брама, ікра, грає, літр, овал, позаду, споруда, ножі, іній, дай,
Життя, кіно, вона, золотий, акація.
![]() Перші букви слів утворять ім’я відомої принцеси.
Перші букви слів утворять ім’я відомої принцеси.
4.Випиши окремо у дві групи іменники, які відповідають на питання що? Та іменники, які відповідають на питання хто?
![]()
![]() Комета, урок, карась, іволга, рукавиці, тракторист, окуляри, чай,
Комета, урок, карась, іволга, рукавиці, тракторист, окуляри, чай,
учень, черепаха, календар, оса, армія, боксер, радість, орел, тітка,
![]() яблуко, ящірка, банан, акація, художник.
яблуко, ящірка, банан, акація, художник.
З перших букв слів утворяться назви двох відомих казок.
![]() 5.Випиши окремо іменники, чоловічого, жіночого й середнього роду (у три стовпчики).
5.Випиши окремо іменники, чоловічого, жіночого й середнього роду (у три стовпчики).
![]() Натхнення, необачність, акула, настрій, ім’я, українець, фантазія,
Натхнення, необачність, акула, настрій, ім’я, українець, фантазія,
Фестиваль, фарбування.
![]() Перші букви слів складуть імена трьох персонажів однієї казки.
Перші букви слів складуть імена трьох персонажів однієї казки.
![]() 6.Випиши іменники, що вживаються тільки в однині.
6.Випиши іменники, що вживаються тільки в однині.
![]() Санча, щастя, іменини, здоров’я, молоко, окуляри, мудрість,
Санча, щастя, іменини, здоров’я, молоко, окуляри, мудрість,
братерство, ножиці, метро, обценьки.
![]() З третіх букв слів складеться назва героя казки Г.К.Андерсена.
З третіх букв слів складеться назва героя казки Г.К.Андерсена.
7.Випиши іменники, вжиті в називному відмінку.
![]()
![]() Посаджу дубок; ромашка зацвіла; маленька іскорка; загасити вогонь;
Посаджу дубок; ромашка зацвіла; маленька іскорка; загасити вогонь;
звучить пісня; сів за стіл; керівник бригади; актриса кіно.
![]() Перші букви слів утворять назву казки.
Перші букви слів утворять назву казки.
![]() 8.Випиши лише віменники, вжиті в родовому відмінку.
8.Випиши лише віменники, вжиті в родовому відмінку.
![]() Пакет сухарів; за кермом автомобіля; зустрічаю гостей; збився з
Пакет сухарів; за кермом автомобіля; зустрічаю гостей; збився з
дороги; лежить на плечі; ремонт квартири; червоні яблука; на дні
озера.
![]() Перші букви слів складуть ім’я казкового героя.
Перші букви слів складуть ім’я казкового героя.
![]() 9.Випишіть лише прикметники, що мають суфікс.
9.Випишіть лише прикметники, що мають суфікс.
![]() Цементний завод; автобусна зупинка; рання пора; тихий голосок;
Цементний завод; автобусна зупинка; рання пора; тихий голосок;
ігрова діяльність; синя стрічка; вишневий сік; нервова система;
![]() старі друзі; авторські права; жирні плями; азартні ігри; брудні руки;
старі друзі; авторські права; жирні плями; азартні ігри; брудні руки;
свіжа газета; акторська професія.
Перші букви слів складуть назву казки.
![]()
![]() 10.Випиши лише слова, в яких немає префіксу.
10.Випиши лише слова, в яких немає префіксу.
Опис, огірок, вікно, відкрити, стіл, стихла, весело, схід, хліб,
дзвінок, донести, стрибок, стерти, скопав.
![]() Останні букви записаних слів утворять назву казки.
Останні букви записаних слів утворять назву казки.
11.Випиши слова, у складі яких є лише корінь (закінчення, суфікс і префікс відсутні).
![]()
![]() Дубок, вчитель, старт, парус, тріск, небо, земля, парад, стіл, мороз,
Дубок, вчитель, старт, парус, тріск, небо, земля, парад, стіл, мороз,
план, день, цирк, диван, шоферський, заклей.
![]() З четвертих букв слів утвориться назва казки Г.К.Андерсена.
З четвертих букв слів утвориться назва казки Г.К.Андерсена.
12.Випиши тільки ті слова, в яких є префікс.
![]()
![]() Помідор, догори, прохід, стілець, обробка, сторінка, вибирати,
Помідор, догори, прохід, стілець, обробка, сторінка, вибирати,
провітрити, закрив, пропис, вітер, виніс, приклеїти, накинув,
![]() передній.
передній.
З перших букв слів складеться казка.
13.Випиши лише дієслова майбутнього часу.
![]()
![]() Зварити, скопаю, допливе, варю, створюватиме, писатимуть,
Зварити, скопаю, допливе, варю, створюватиме, писатимуть,
малює, згорну, понадкушую, підігріти, проситимеш, збивати,
підійти, погодує, зшиємо, включу, люблю, копатимеш.
![]() Другі букви слів утворять назву української казки.
Другі букви слів утворять назву української казки.
![]()
![]() 14.Випиши дієслова, вжиті в неозначеній формі.
14.Випиши дієслова, вжиті в неозначеній формі.
Смоктати, зварити, гримить, варити, учитися, спечуть, думати,
спишуть, схилитися, несуть, намалювати, біжить, спить.
![]() З других букв складеться назва дійовох особи багатьох казок.
З других букв складеться назва дійовох особи багатьох казок.
![]() 15.Випищіть дієслова першої дієвідміни.
15.Випищіть дієслова першої дієвідміни.
![]() Думаю, стою, лечу, біжу, граю, слухаю, роблю, бігаю, малюю,
Думаю, стою, лечу, біжу, граю, слухаю, роблю, бігаю, малюю,
люблю, співаю.
![]() Треті букви слів складуть ім’я відомого казкового героя
Треті букви слів складуть ім’я відомого казкового героя
Зарубіжного автора.
Пригадай казку
1.Запиши 10 іменників з казки О.Толстого «Золотий ключик, або Пригоди Буратіно», що відповідають на питання «хто?»
2.Запиши 10 іменників з казки Г.К.Андерсена «Гидке каченя» і постав у них знак наголосу.
3.Добери 10 прикметників для характеристики одного з казкових персонажів казки О.Толстого «Золотий ключик, або Пригоди Буратіно»:
а) Буратіно (який?) …, …;
б) Карабас-Барабас (який?) …, … .
4.Запиши 5 іменників жіночого роду з казки «Ріпка», вжившиїх у давальному відмінку.
Закінчення іменників виділи.
5.Запиши 5 іменників з казки Ш.Перро «Попелюшка», вживши їх у місцевому відмінку.
6.Добери 10 прикметників для характеристики Попелюшки.
Попелюшка (яка?) …, … .
7.Запиши казки у назві яких є числівники.
8.Що доводилося робити казковій дівчиці Попелюшці?
Запиши 10 дієслів в неозначеній формі.
9.Запиши 5 словосполучень (іменник з прикметником) з казки Г.К.Андерсена «Снігова королева».
Зразок: королева (яка?) снігова.
10.Запиши 5 сполучень слів (іменник з дієсловом) з казки О.С.Пушкіна про золоту рибку.
Зразок: рибка (що зробила?) припливла.
Кросворди
1.Впиши слова по горизонталі та прочитай у виділених клітинках по вертикалі назву казки:
1) «риба» з суфіксом;
2) «кішка» чоловічого роду»
3) «плечі» в однині;
4) «очі» в однині;
5) «жабка» без суфікса.
(Ріпка.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.Впиши слова-антоніми по горизонталі та прочитай у виділених клітинках по вертикалі назву персонажа багатьох казок:
1) антонім слова «чорний»;
2) антонім слова «далеко»;
3) антонім слова «смуток»;
4) антонім слова «свійський»;
5) антонім слова «безділля»;
![]()
![]()
![]()
![]()
![]()
![]() (Лиска.)
(Лиска.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.Впиши по горизонталі синоніми поданих слів і у виділених вертикальних клітинках прочитай ім’я однієї казкової шахрайки:
1) алфавіт;
2) парус;
3) горизонт;
4) аплодисменти;
5) водограй;
(Аліса.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.Впиши слова по горизонталі й у виділених вертикальних клітинках прочитай ім’я одного з відомих казкових ледарів:
1) неозначена форма від дієслова «плаче»;
2) «варити» в 2 особі однини теперішнього часу;
3) «павук» із суфіксом;
4) спільнокореневий іменник від дієслова «жити»;
5) прикметник від «воля».
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Круть.)
(Круть.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.Впиши по горизонталі неозначену форму від поданих дієслів і прочитай назву виду усної народної творчості:
1) тікав;
2) беру;
3) кажуть;
4) печу;
5) сплю.
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Казка.)
(Казка.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Уривки з казок з граматичними завданнями
1.Послухалася баба, пішла в хи…ку, назмітала в засіку борошенця, витопила в п…чі, замісила гарненько тісто, сп…кла колобок та й поклала на вікні, щоб прост…гав.
А він – з вікна на пр…ьбу, з при…ьби на землю та й покотився дорогою. («Колобок».)
Завдання.
1.Вставити пропущені букви.
2.Підкреслити дієслова.
3.Знайти й виписати слова, що мають префікси.
2.Ж…ли собі двоє м…шенят – Круть і Верть та півник Голосисте Горлечко. М…щенята було тільки й знають, що танцюють та співають. А півник удосвіта встане, всіх піснею збудить та й до роботи б…реться. Ото якось підмітав у дворі та й знайшов пшеничний колосок. («Півник та двоє мишенят».)
Завдання.
1.Вставити пропущені букви.
2.Пояснити вживання великої букви.
3.Підкреслити іменники.
3.Жили собі дід та баба. Дід служив на майдані майданником, а баба сиділа вдома, мички пряла. І такі вони бідні – нічого не мають: що зароблять, то проїдять та й нема.
От баба й напалась на діда:
– Зроби та й зроби мені, діду, солом’яного бичка й осмоли його смолою. («Солом’яний бичок».)
Завдання.
1.Знайти спільнокореневі слова.
2.У другому реченні підкреслити головні члени речення.
3.Знайти спонукальне речення.
4.Зібралися одного разу звірі докупи й почали радитися між собою, кого їм обрати царем, щоб був порядок, щоб мали вони правдивого суддю. Були там Слон, Лев, Тигр, Верблюд, Ведмідь, Вовк, Олень, Лисиця, Заєць, Дикий кабан, Зебра, Коза, Кінь, Корова, Собака, Качка й інші звірі, які жили тоді на світі; либонь, був і Осел. («Цар Лев».)
Завдання.
1.Виписати іменники чоловічого роду.
2.У двоскладових словах позначити наголос.
5.У Києві над Дніпром живе Кожум’яка на ймення Кирило. Як вийде на Дніпро мочити шкури, то не одну несе, а дванадцять разом. Як набрякнуть ті шкури водою в Дніпрі, то я візьму та й учеплюся за них – чи витягне? А йому байдуже: як потягне, то й мене з ними трохи на берег не витягне. («Кирило Кожум’яко».)
Завдання.
1.Пояснити вживання великої букви.
2.Підкресліть дієслова, вжиті в майбутньому часі.
Розділ III.Герої казок прийшли на урок…
***
До нас сьогодні на урок
Прийшов казковий Колобок.
Від вовка він тікає,
Бо в нього той питає.
1.Як утворити прикметник від іменника «вовк»?
2.Як розібрати цей прикметник за будовою?
3.Які ще спільнокореневі слова можна дібрати до слова «вовк»?
4.Як поділити на склади слово «Колобок», вжите в множині?
![]()
![]()
![]()
![]() 5.Будова яких з поданих слів не відповідає моделі: ?
5.Будова яких з поданих слів не відповідає моделі: ?
Вовчиця, вовченя, вовчий, вовчисько, вовкам.
***
Це королева снігова,
Хоч на малюнку, не жива,
Та нам від неї йдуть погрози:
На нас напустяться морози,
Коли не виконає враз
Її завдань наш дружний клас!
1.Знати спільнокореневі серед поданих слів.
Морок, морозиво, морква, заморозки, заморський, холодильник, крига, розморозити.
2.Знайти слова, будова яких відповідає поданим звуковим моделям:
а)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Хуртовина, хурделиця, вітер, мороз, північ, крижаний, морозець, сніговий.
3.Провідміняти слово «іній».
4.Підібрати 10 прикметників до іменників:
Сніг (який?) …, …;
Вітри (які?) …, …;
Зима (яка?) …, … .
4.Вказати відмінок іменників:
з Півночі; на півночі; на північ; холодна північ.
***
Карабас-Барабас
Подає у суд на нас,
На П’єро і Буратіно,
Артемона і Мальвіну,
Ми програємо процес
Якщо не там напишем «С»!
(С, з) …хилитис, …тримати, …формулювати, …горнути, …пакувати, …хибити, …шити, …пізнився, …калічений, …тривожено, ро…тривожений, бе…культурний, бе…коштовний, …пантеличений.
***
Ох, які ж важкі завдання
Надіслал на урок
Нам цариця Помилиця
З царства грубих помилок!
Не підкоримось цариці!
Доведемо Помилиці:
Ми не неуки лякливі,
А розумники сміливі!
1.Вставити пропущені букви.
Кор…дор, тра…вай, небе…печно, про…ьба, ні…ті, ж…нка, велос…педист, сант…метр, ч…мпіон, гор…зонт, парт…занський, порт…єра, ш…тка, х…мічний, ш…десят.
2.Дописати закінчення.
На доаг… ниві; під висок…соснами; довговух… зайців; і тих… пісні; на вузьк… стежці; для дорог… гостей; без важк… речей; чоловіч… одяг; жіноч… туфлі; циганськ… пісні; з далек… доріг; довг… ночами; в українськ… казці.
3.Вставити, де потрібно, подвоєні букви.
Зелен…ю, сткатерт…ю, північ…ю, нехворощ…ю, жит…ям, лист…ям, без доріж…ям, безробіт…ям, стат…ею, суд…ею, мужніст…ю, радіст…ю.
4.Вставити, де треба, апостроф.
Дев…яносто, пуп…янки, підв…язаний, свя…тковий, мавп…ячий, цв…ях, комп…ютер, під…йом, об…ємний, від…ємник, з…йомка, мураі…їний, моркв…яний, тьм…яний, прем…єра, кар…єра.
5.Дописати закінчення.
Сильн… біль, довг… путь, широк… степ, густ… вуаль, нов…. Тюль, дорог… шампунь, висок… рівень, алергічн… нежить, вищ… ступінь, далек… подорож, гаряч… какао.
***
У Баби-Яги до нас
Запитання є щораз.
Нічогісінько не знає –
І тому про все питає.
1.Як утворити множину від слів: родич, колір, пляшка, дах, звір, око, вухо, хліб, комар, маляр, ім’я, тиждень, мило, крем, папір.
2.Які з поданих іменників не мають форми множини?
Небо, бруд, чистота, зло, добро, здоров’я, щастя, радість, зелень, метал, золото, іній, дощ, просо, рис, борошно.
3.Які з поданих іменників не мають форми однини?
Двері, вікна, сани, штани, погони, капці, колготки, панчохи, шкарпетки, ножиці, обценьки, близнюки, гроші, меблі, граблі, сутінки.
![]()
![]() 4.Як привильно казати?
4.Як привильно казати?
![]()
![]() Запитання чи запитання?
Запитання чи запитання?
![]()
![]() Черговий чи черговий?
Черговий чи черговий?
![]()
![]() Випадок чи випадок?
Випадок чи випадок?
Центнер чи центнер?
П’ять кілограм чи п’ять кілограмів?
Два ящики чи два ящика?
Протягом тижня чи на протязі тижня?
Примуть участь чи візьмуть участь?
Сторона квадрата чи сторона квадрату?
Дружня розмова чи дружна розмова?
Дружний клас чи дружній клас?
***
Коли по допомогу
Звертаються коти,
Та щей коти казкові,
Нам слід допомогти.
Матроскін нас питає.
Допоможіть, хто знає!
1.Чи потрібен апостроф у словах дерев…яний і моркв…яний?
2.Як правильно писати: морозиво чи морозиво; мереживо чи мережево?
3.Як правильно: пляшка кефіру, пляшка кіфіру чи пляшка кефіра?
4.Якого роду іменник листоноша?
5.В якому слові звуків більше: вмиваєшся чи вмивається?
***
Принцеса Білосніжка
Прийшла сьогодні в клас,
Завдання й запитання
У неї є для вас.
1.Як у місцевому відмінку писати слова.
Білосніжка, книжка, ліжко, мішок, горішок, молоко, ягнятко.
2.Написати словами: у 16 квартирі, з 9 друзями, до 7 гномів.
3.Дописати закінчення: два ящик…, п’ять кілограм…, три мішк…, чотири сантиметр…, шість помідор…, сім центнер…, три дуб…, 24 тюльпан… .
4.Розібрати слова за будово.
Верхня, зверху, вершина, вершник, поверх, верхівка, поверхово, верхи (на коні).
Пекти, печиво, пекар, пекарський, запікання, спекти, пекарня, спечу.
***
До нас Незнайко завітав,
І от про що він запитав.
![]()
![]()
![]() 1.Як правильно: один туфель, одна туфля, чи одна туфля?
1.Як правильно: один туфель, одна туфля, чи одна туфля?
2.Як правильно: один капець чи одна капця?
3.Як правильно: вийшов із будинку чи з будинка? з метра чи з метро?
4.Як правильно: я не користуюся бігудями чи не користуються бігуді?
А може, бігудьми?
5.Як правильно писати:
Не забаром канікули;
Незабаром канікули;
Не за баром канікули?
6.Чи не зробив Незнайко помилки?
Незнайко робе уроки;
Незнайко варе борщ;
Незнайко любе співати.
***
Лікар Айболить до нас
Завітав сьогодні в клас.
Хитре запитання має:
Хто «його» слова впізнає?
Ліки, лічильник, лікувати, лічити, перелік, лікарня, лікоть, незліченний, лікарський, відлік, лікувальний.
1


про публікацію авторської розробки
Додати розробку
