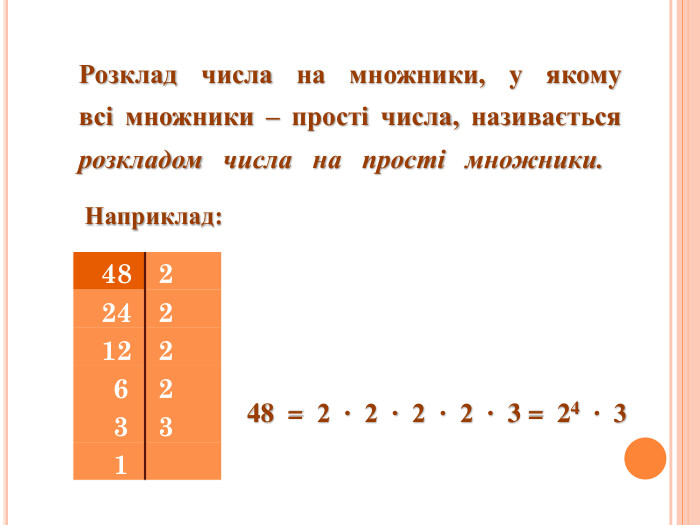
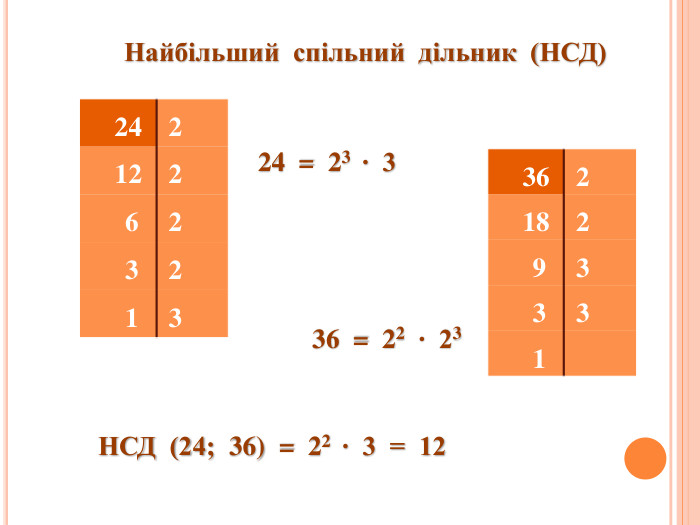
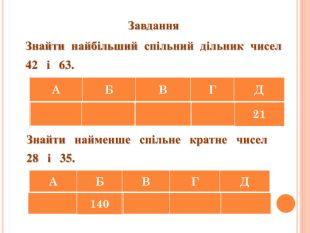
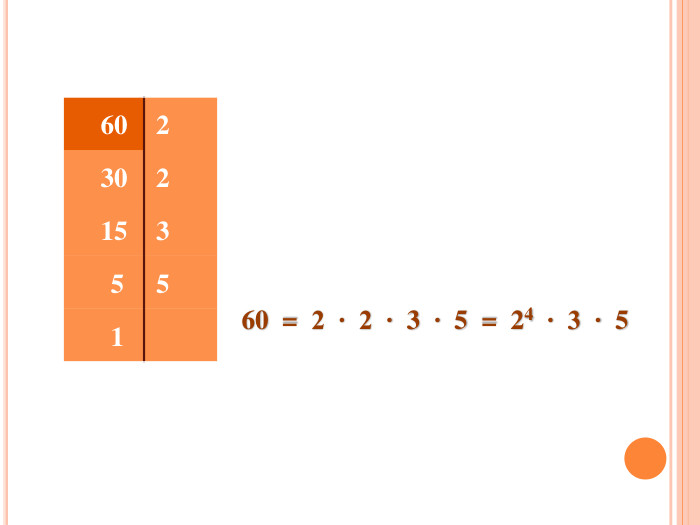Розкладання чисел на прості множники
Про матеріал
Презентацію створено з метою повторення матеріалу та подолання освітніх втрат. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку