Тема уроку. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини.

Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини.

Обладнання: стереометричний набір, моделі куба і тетраедра, схема «Аксіоми стереометрії».

Хід уроку

І. Аналіз виконання тематичного оцінювання № 1.

II. Перевірка домашнього завдання

Зібрати зошити наприкінці уроку для перевірки їх ведення і вико­нання домашнього завдання.

III. Узагальнення та систематизація знань учнів

Взаємне розміщення прямої і площини в просторі

Запитання до класу.

1. Згадайте і сформулюйте теорему про належність площині прямої, дві точки якої належать площині.
2. Як можуть розміщуватися пряма і площина в просторі?

При обговоренні цього питання доречно скористатися схемою «Взаємне розміщення прямої і площини» з уроку № 3, с. 21.

IV. Сприйняття й усвідомлення нового матеріалу

Поняття прямої, паралельно! площині, та ознака паралельності прямої і площини

Пряма і площина називаються паралельними, якщо вони не

мають спільних точок.

Паралельність прямої а і площини α позначається так: а || . Наочне уявлення про пряму, яка паралельна площині, дають лінії перетину стіни і стелі — ці лінії паралельні площині підлоги. Відрізок називається пара­лельним площині, якщо він є частиною прямої, паралельної площині.

Сформулюємо та доведемо ознаку паралельності прямої і площини.

Теорема.

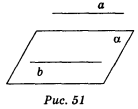Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.

• Доведення ознаки записується на дошці і в зошитах.

Дано: а || b; b α (рис. 51).

Довести: а || .

Доведення

Припустимо, що пряма а не належить площині  . Тоді а і  мають спільну точку А.

Якщо А  b , то а і b мають спільну точку А, що суперечить умові.

Якщо А  b , то а і b мимобіжні, що суперечить умові.

Отже, а ||  .

Виконання вправ

1. Дано зображення куба АВСD₁А₁B₁С₁D₁. Доведіть, що:

а) пряма АВ паралельна площині DСС₁;

б) пряма АВ паралельна площині DСВ₁.

2. У трикутній піраміді SАВС точки М і N — середини ребер SА і SВ відповідно. Доведіть, що МN || (АВС).

3. Дано площину  і поза нею точку А. Провести через точку А пря­му, паралельну даній площині  .

Розв'язання

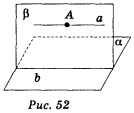
Аналіз. За умовою А   (рис. 52). Щоб пряма а, яка проходить через точку А, була паралельна площині , достатньо, щоб вона була паралельна прямій b, яка належить площині  . Звідси випливає план розв'язання:

1) в площині  проводимо довільну пряму b;

2) через пряму b і точку А проводимо площину ;

3. через точку А проводимо пряму а: а || b.

Доведення. Згідно з ознакою паралельності прямої і площини маємо: а ||  .

Дослідження. Пряма b проведена в площині  довільно, таких прямих нескінченна множина, отже, задача має нескінченну множину розв'язків.

4. Дано пряму а і точку А, яка не лежить на ній. Провести площину, яка проходить через точку А і паралельна прямій а.

5. Дано паралельні прямі а і b. Провести через пряму а площину, яка паралельна прямій b.

6. Задача № 15 із підручника (с. 19).

7. Дано мимобіжні прямі а і b та точку С, яка не лежить на них. Про­вести через точку С площину, паралельну прямим а і b.

V. Домашнє завдання

§ 2, п. 9; контрольні запитання № 5, 6; задачі .№ 14, 16 (с. 19).

VI. Підведення підсумку уроку

 Запитання до класу

1) Як можуть розташовуватися пряма і площина у просторі?

2) Сформулюйте ознаку паралельності прямої і площини.