Тема уроку.  Розв'язування задач на ознаку паралельності прямої і площини.

Мета уроку: формування вмінь учнів застосовувати ознаку паралельності прямої і площини до розв'язування задач.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

1. Два учні на відкидних дошках відтворюють розв'язання задач № 14, 16. У цей час клас виконує математичний диктант.

2. Математичний диктант.

Дано зображення куба: варіант 1 — рис. 53, варіант 2 — рис. 54.

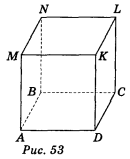
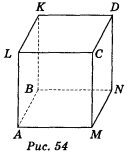
Користуючись зображенням, запишіть:

1. пряму, яка паралельна площині ВСМ і проходить через точку D; (2 бали)
2. грані куба, які паралельні прямій СD; (2 бали)
3. площину, яка містить пряму ВN і паралельна прямій СD; (2 бали)
4. площину, яка паралельна прямій СD і проходить через точку К; (2 бали)
5. площини, які паралельні прямій ВМ; (2 бали)
6. прямі, паралельні площині АВМ. (2 бали)

Відповідь. Варіант 1.1) АD; 2) АВNМ і МNLК; 3) АВN; 4) КМN і АВК; 5) DСК, LСА, КDM; 6) КL, LС, СD, КD, КС, DL.

  Варіант 2.1) DN; 2) АВКL, АВNМ; 3) АВN; 4) АВК і КLМ; 5) СDК, КCN, КСА; 6) KL, LС, СD, KD, KС, DL.

3. Провести колективне обговорення результатів роботи на відкидних дошках, написання математичного диктанту.

II. Узагальнення та систематизація знань учнів

Властивості прямої і площини, які паралельні між собою

Доцільно розглянути такі задачі на доведення.

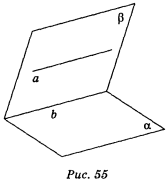
1. Доведіть, що якщо площина проходить через пряму, яка паралель­на другій площині, і перетинає цю площину, то пряма перетину па­ралельна даній прямій.

Розв'язання

Нехай а ||  (рис. 55) і площина  проходить через а, b — пряма пере­тину площин  і  . Доведемо, що а || b. Прямі а і b лежать в одній площи­ні  і не перетинаються, бо в супротивному випадку пряма а перетинала б площину , що неможливо, оскільки згідно з умовою а ||  . Отже, а || b.

2. Доведіть, що якщо через кожну із двох паралельних прямих прове­дено площину, причому ці площини перетинаються, то їх лінія пе­ретину паралельна кожній із даних прямих.

Розв'язання

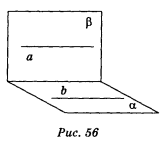Нехай а || b, пряма а лежить в площині  , пряма b лежить в площині , площини  і  перетинаються по прямій с (рис. 56). Доведемо, що а || с , b || с . Оскільки а || b і пряма b лежить в площині , то а ||  і, отже, згідно з розв'язуванням задачі 1, а || с. Аналогічно, оскільки а || b, а ле­жить в площині , b ||  і, отже, b || с. Таким чином, а || с і b || с .

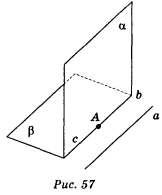
3. Доведіть, що якщо дві площини, що перетинаються, паралельні од­ній і тій самій прямій, то пряма перетину цих площин паралельна даній прямій.

Розв'язання

Нехай  і  перетинаються по прямій с, а ||  , а ||  (рис. 57). Дове­демо, що а ||  с. Візьмемо на прямій с довільну точку А і через неї прове­демо пряму b, паралельну прямій а. Оскільки пряма а || , а || , то пряма b лежить як в площині , так і в площині . Отже, пряма b — пряма, по якій перетинаються площини  і , тому пряма b збігається з прямою с, отже, с || а .

III. Закріплення та осмислення знань учнів

Розв'язування задач

1. Задача № 13 (1, 4) із підручника (с. 19).

2. Площина  і пряма а паралельні одній і тій же прямій b. Доведіть: якщо пряма а не лежить в площині , то а ||  .

3. Доведіть, що всі прямі, які перетинають одну із мимобіжних пря­мих і паралельні другій, лежать в одній площині.

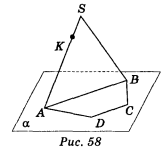4. Трапеція АВСD (АВ || СD) лежить у площині  (рис. 58), АВ = 12 см. Поза площиною  взяли точку S і на відрізку SА відмітили то­чку К таку, що АК:КS=3:1. Побудуйте точку Х — точку пере­тину площини DКС і відрізка SВ і знайдіть довжину відрізка КХ.

5. Задача № 17 із підручника (с. 19).

IV. Домашнє завдання

§ 2, п. 9; задачі № 13 (2, 3), 22 (с. 19—20).

V. Підведення підсумку уроку

Запитання до класу

1) Сформулюйте ознаку паралельності прямої і площини.

2) Сформулюйте твердження, обернене до ознаки паралельності пря­мої і площини. Чи правильне воно?

3) Закінчіть твердження.

а) Якщо площина проходить через пряму, що паралельна другій площині, і перетинає цю площину, то пряма перетину ... .

б) Якщо через кожну із двох паралельних прямих провести площи­ни, які перетинаються, то їх лінія перетину ... .

в) Якщо дві площини, які перетинаються, паралельні одній і тій са­мій прямій, то пряма перетину цих площин ... .