Розрахунок параметрів вільного об’єму полімерних систем

ЗМІСТ

 

ВСТУП 

РОЗДІЛ І. ТЕОРІЇ ВІЛЬНОГО ОБ’ЄМУ ПОЛІМЕРНИХ СИСТЕМ 

Вільний об’єм та його характеристики 

Особливості вільного об’єму полімерних систем 

РОЗДІЛ ІІ. ПАРАМЕТРИ ВІЛЬНОГО ОБ’ЄМУ ПВХ-СИСТЕМ 

Вільний об’єм пластифікованих і металонаповнених композицій на основі ПВХ 

Методи досліджень

Дослідження впливу силових полів на параметри вільного об’єму полівінілхлоридних композицій             

ВИСНОВКИ 

ЛІТЕРАТУРА 

ДОДАТКИ

ВСТУП

 

Актуальність проблеми.Полімерні матеріали і композиції на їх основі – складні системи, утворені підсистемами, що складаються із структурних елементів різної природи, масштабу і ступеню автономності. Це призводить до виникнення специфічних надмолекулярних структур і, як наслідок, великого набору різних форм рухливості структурних одиниць.

Вільним об’ємом володіють як низькомолекулярні (рідини, кристалічні та аморфні тверді тіла), так і високомолекулярні. У рамках концепції вільного об’єму знаходять своє пояснення на молекулярному рівні багато закономірностей, що спостерігаються в полімерах та композиціях на їх основі. Однак в останньому випадку ми зустрічаємося з рядом специфічних особливостей, зумовлених, зокрема, сегментальною рухливістю полімерних макромолекул та релаксаційною природою динамічних процесів. Тому існуючі теорії вільного об’єму, які в багатьох випадках дають задовільне пояснення процесів, що відбуваються в низькомолекулярних системах, при застосуванні до полімерів і композицій на їх основі часто зустрічаються з певними труднощами – насамперед у плані співвідносності кількісного та якісного аналізу. Тому питання, що стосуються залежності характеристик вільного об’єму від структурних та енергетичних параметрів полімерних систем, а також впливу різного роду модифікуючих факторів, викликають цілком зрозумілий інтерес і потребують подальшого вивчення.

Дослідження поведінки параметрів вільного об’єму в залежності від природи і властивостей наповнювачів, пластифікаторів та зовнішніх силових полів дає можливість не тільки глибше зрозуміти природу процесів релаксації у полімерних системах, але й наблизитися до розв’язання проблеми найбільш раціонального поєднання їх найважливіших властивостей.

Мета і задачі досліджень.

• Проаналізувати теорії вільного об’єму речовин з точки зору їх застосування до пояснення фізичних властивостей лінійних полімерів та їх систем.
• На основі модельних підходів проаналізувати взаємозв’язок параметрів вільного об’єму композицій з їх релаксаційними властивостями, структурними та енергетичними характеристиками.
• На основі отриманих експериментальних і теоретичних даних розглянути перспективи напрямленого регулювання та прогнозування комплексу властивостей гетерогенних полімерних систем.

Предметом досліджень стали особливості структурної організації полімерних композитів в присутності дрібнодисперсних наповнювачів.

Об’єктами досліджень вибрані структурно-чутливі параметри вільного об’єму полімерних систем в залежності від природи модифікуючих факторів.

 

 

 

 

 

 

 

РОЗДІЛ І

ТЕОРІЇ ВІЛЬНОГО ОБ’ЄМУ ПОЛІМЕРНИХ СИСТЕМ

1.1.               Вільний об’єм та його характеристики

 

Як правило під вільним об’ємом рідини розуміють порожній простір між молекулами, тобто нещільності, або «дірки» молекулярних (мономерних) розмірів, пов’язаних з нерегулярною упаковкою молекул. Я.І. Френкель  на основі термодинамічних міркувань показав, що в кристалах також можуть бути молекулярні нещільності. Однак вільні об’єми кристалів та рідин мають різну природу. Вільний об’єм кристала зумовлений асиметрією коливань частинок і розподілений між ними неперервно. Вільний об’єм рідини складається з двох частин: неперервної, яка визначається коливаннями молекул в рідині, та дискретної, зумовленої існуванням порожнин. Дискретна частина робить можливим постійний обмін місцями частинок, тобто «дірки» в рідині носять флуктуаційний характер.

Розглянемо поняття вільного об’єму на якісному рівні.

З підвищенням температури вільний об’єм зростає. Коефіцієнт термічного розширення речовин, по суті, залежить від температурної зміни вільного об’єму. У рідин він завжди більший, ніж в кристалічних тілах.

Експериментальне визначення вільного об’єму речовини є досить складною задачею. Як правило його розраховують, користуючись графічною залежністю питомого об’єму речовини від температури (рис. 1.3).

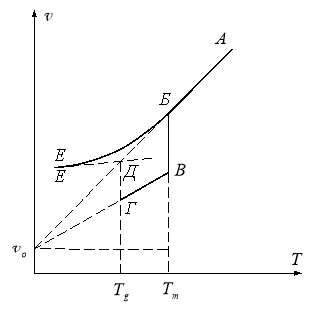
Рис. 1.3. Залежність питомого об’єму речовини від температури.

 

Пряма АБ відповідає температурній зміні питомого об’єму рідини. В точці Б відбувається фазове перетворення – утворюється кристалічна фаза, об’єм змінюється стрибкоподібно до точки В (об’єм кристала). З подальшим охолодженням об’єм зменшується по прямій ВГ. Пряма АБ має більший нахил, ніж пряма ВГ. Можна припустити, що з наближенням до температури абсолютного нуля вільний об’єм стає рівним нулю. Тому значення зайнятого об’єму отримують екстраполяцією прямої ВГ до осі ординат.

При швидкому охолодженні рідини нижче температури плавлення її можна отримати в переохолодженому стані. За подальшого охолодження рідина твердне, не утворюючи кристалічної фази, тобто переходить у склоподібний стан; об’єм при цьому змінюється монотонно. Точка перетину прямих АБ і ДЕ відповідає температурі силування , яка завжди нижча температури кристалізації даної речовини. З рисунка видно, що при одній і тій же температурі вільний об’єм речовини в нерівноважному склоподібному стані більший вільного об’єму кристалічного тіла.

Поняття вільного об’єму речовини тісно пов’язане з поняттям щільності упаковки її молекул.

Щільність упаковки кількісно оцінюється так званим коефіцієнтом упаковки, який являє собою відношення власного об’єму молекул до істинного об’єму тіла, утвореного цими молекулами. Власний об’єм молекул розраховується теоретично, виходячи з хімічної будови речовини, тобто за відомими значеннями радіусів атомів, які входять до складу молекули.

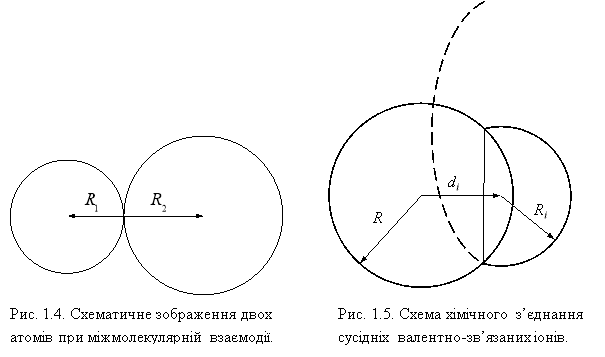
При цьому вважається, що валентно не зв’язані атоми, які вступають в міжмолекулярну (а не хімічну) взаємодію, дотикаються один до одного по границях сфер. Це схематично показано на рис. 1.4.

Хімічна взаємодія двох атомів завжди призводить до їх ущільнення, оскільки довжина хімічного зв’язку завжди менша, ніж сума двох міжмолекулярних радіусів (рис. 1.5):

.

 

Якщо відомі міжмолекулярні радіуси для всіх атомів, що входять до ланки полімера, яка повторюється, а також всі довжини хімічних зв’язків між цими атомами, можна розрахувати власний (Ван-дер-Ваальсовий) об’єм елементарної ланки і побудувати модель цієї ланки (чи більшого фрагменту макромолекули), де об’єм кожного атома окантований сферою з міжмолекулярним радіусом .

Очевидно, що об’єм даного атома залежить від його оточення. Чим більший об’єм сусіднього, хімічно зв’язаного атома, і чим менша довжина хімічного зв’язку, тим більше ущільнюється даний атом.

На основі уявлень про молекулярну упаковку, міжмолекулярні радіуси і довжини зв’язків розраховуються густина, температура склування та інші характеристики аморфних полімерів .

В рамках теорії вільного об’єму знаходять своє пояснення цілий ряд фізичних процесів, які відбуваються у невпорядкованих склоподібних системах. До їх числа, насамперед, слід віднести термодинамічні теорії склування, дірково-активаційний процес в’язкої течії. При цьому, однак, незважаючи на якісне та кількісне узгодження розрахункових значень фізичних характеристик, отриманих із застосуванням теорії вільного об’єму, не завжди вдавалося ідентифікувати структурні елементи, що відповідають за прояви тих чи інших властивостей. Так само виникали певні розбіжності у трактуванні енергетичних параметрів, які пов’язувалися з характеристиками вільного об’єму. Ці та ряд інших питань у деякій мірі можуть бути пояснені різними підходами до самого трактування поняття вільного об’єму.

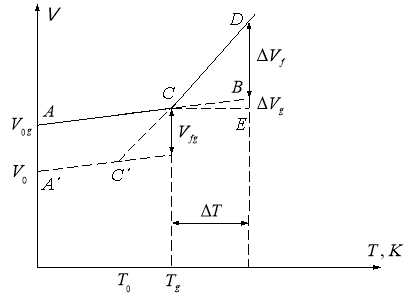
Рис. 1.6. Температурна залежність об’єму аморфної речовини при стандартній температурі нагрівання: АВС – теплове розширення скла; CD – теплове розширення рідини.

 

Дійсно, об’єм склоподібного тіла складається з трьох частин:

                                                   (1.1)

де V₀ – рівноважний об’єм при 0 К; V_T і V_f – складові об’єму, що залежать від температури: V_T – «коливний» об’єм, який виникає внаслідок ангармонізму (теплового розширення тіла); V_f – флуктуаційний вільний об’єм, який виникає шляхом утворення «дірок» (рис. 1.6):

  при ,

      при ,

де , , – флуктуаційний вільний об’єм при температурі склування, f_g – його відносна частка, α_f – коефіцієнт теплового розширення вільного об’єму.

Зміст температури видно з рис. 1.6, де пряма A′C′ виражає температурну залежність (V₀ + V_T). В дійсності через скінченну швидкість охолодження скло при абсолютному нулі має об’єм не V₀, а V_0g, оскільки різницю вносить флуктуаційний вільний об’єм, заморожений при температурі склування:

.

Різницю V_T = V – V₀ називають вільним об’ємом теплового розширення, а величину V_F = V – V_d, (V_d – власний об’єм молекул) – геометричним вільним об’ємом. Для багатьох аморфних речовин поблизу температури склування (V – V₀)/V ≈ 0,1 і (V – V_d)/V ≈ 0,3, тобто геометричний вільний об’єм, який є «порожнім» простором між частинками, приблизно на порядок більший флуктуаційного вільного об’єму: V_fg/_V ≈ 0,03. У неорганічних стекол, полімерів та інших склоподібних розплавів, де наявні ковалентні, водневі та інші напрямлені зв’язки, кінетичні одиниці «зв’язані» і їм доступна лише невелика флуктуаційна частина геометричного вільного об’єму, а решта порожнього простору між молекулами не відіграє жодної ролі в переміщенні кінетичних одиниць при в’язкій течії. Тому молекулярна рухливість рідини визначається в основному флуктуаційним вільним об’ємом.

2.           Особливості вільного об’єму полімерних систем

Результати експериментальних і теоретичних досліджень в області невпорядкованих структур засвідчують, що в таких системах проявляються певні універсальні властивості, обумовлені визначеними загальними динамічними закономірностями в склоподібних речовинах, хоча за морфологіями структур вони різні. За останні роки з'явилися моделі кінетичних явищ у склоподібних системах, що мають достатню універсальність і не спираються на конкретну хімічну природу цих систем. Вони ґрунтуються на деяких базових принципах, які дозволяють врахувати ефекти кооперативності та неоднорідності структури склоподібних систем.

На роль одного з таких загальних феноменологічних підходів може претендувати теорія вільного об’єму. При цьому, однак, фізичний зміст параметрів моделі багато в чому залишається неясним. Це особливо проявляється у випадку полімерів та композицій на їх основі, де найбільшого поширення набули діркова та дірково-кластерна теорії вільного об’єму та їх модифікації.

Структура аморфного стану склоподібних полімерів є однією з найважливіших і найбільш дискусійних проблем фізики полімерів. Вперше було висунуто припущення про існування в полімерах ближнього (локального) порядку, в основу якого були покладені порівняння сегментального об’єму і густини аморфної фази, ефект твердофазної кристалізації. Згідно сучасних уявлень склоподібне тверде тіло розглядається як мікронеоднорідне середовище, що складається з двох динамічних компонент: упорядкованих областей (кластерів), розташованих у невпорядкованому середовищі (рихлоупакованій матриці). При зовнішньому впливі кластери зазнають перебудови, що виражається в дифузійному обміні флуктуаційними дірками – збудженими кінетичними одиницями між цими компонентами: кластерами і рихлоупакованою матрицею.

Згідно кластерної моделі флуктуаційний вільний об’єм концентрується в рихлоупакованій матриці. В термінах теорії вільного об’єму відрив кінетичної одиниці (атома, групи атомів) від кластера означає утворення флуктуаційної мікропорожнини («дірки»), а приєднання кінетичної одиниці до кластера – її замикання. Тому флуктуаційна зміна вільного об’єму з температурою може бути, в принципі, реалізована при сталому об’ємі системи в результаті обміну «дірками» між кластерами і рихлоупакованою матрицею. За такого підходу до механізму народження та міграції флуктуаційних мікропорожнин долається утруднення в поясненні температурної залежності в’язкості при фіксованому об’ємі системи.

Критична частка флуктуаційного вільного об’єму , яка відповідає температурі склування, визначається, наприклад, за даними про в’язкість в області склування. Знаючи , можна розрахувати енергію утворення мінімальної мікропорожнини:

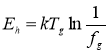.                                                    (1.8)

Енергія утворення дірки кДж/моль близька до енергії міжмолекулярної взаємодії. Утворення дірки в таких системах обумовлене граничною деформацією міжмолекулярних зв'язків між ділянками – ланками макромолекул. Радіус мікропорожнини вільного об’єму в епоксидних полімерах складає в середньому 6,5 Å. За даними позитронної спектроскопії він дещо менший.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ ІІ
ПАРАМЕТРИ ВІЛЬНОГО ОБ’ЄМУ ПВХ-СИСТЕМ

Вільний об’єм металонаповнених композитів на основі ПВХ

 

Введення в об’єм полімера низькомолекулярних домішок здатне суттєво змінити найважливіші експлуатаційні показники матеріалу. Оскільки полімер є складною системою, що складається із сукупності структурно підпорядкованих взаємодіючих підструктур, то зміни, що супроводжують такого роду структурну модифікацію, в тій чи іншій мірі проявляються на всіх морфологічних рівнях композиту.

Це  стосується і параметрів вільного об’єму, оскільки вони пов’язані з характеристиками, що формують комплекс властивостей полімерів.

З метою вияснення такого впливу досліджували температурні та концентраційні залежності величини і відносної частки флуктуаційного вільного об’єму систем на основі полівінілхлориду.

На рис. 2.1 представлені концентраційні залежності величини і відносної частки флуктуаційного вільного об’єму композицій ПВХ+Fe₃O₄ і ПВХ+W.

Їх аналіз показує, що вказані наповнювачі по-різному впливають на параметри вільного об’єму полівінілхлориду. Якщо для систем, модифікованих оксидом заліза спостерігається монотонне збільшення величин V_f і f в усій області концентрацій, то для систем з вольфрамом після досягнення максимуму при об.% наповнювача значення V_f і f починають зменшуватися.

Це може бути пояснене структурними змінами, що відбуваються в композиціях під впливом дрібнодисперсних наповнювачів, насамперед у межових шарах. В області малих концентрацій (від 0 до 0,5 об.%) відбувається інтенсивне формування граничних шарів композицій обох типів, що створює додаткові можливості для збільшення вільного об’єму. В подальшому, однак, структурні зміни в композиціях ПВХ+Fe₃O₄ і ПВХ+W супроводжуються якісно різною поведінкою параметрів флуктуаційного вільного об’єму. Їх зростання у першому випадку свідчить про зменшення коефіцієнту упаковки макромолекул ПВХ в граничних шарах, що зумовлено збільшенням об’ємного вмісту і зменшенням густини і ефективної товщини останніх. Цей процес супроводжується зростанням об’єму флуктуаційних мікропорожнин (рис. 2.2).

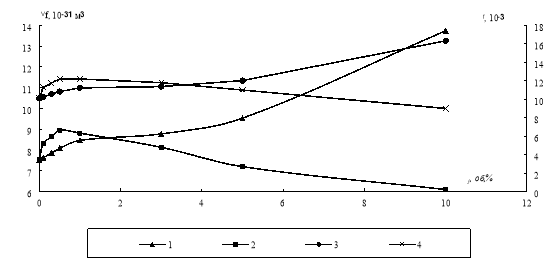
Рис. 2.1. Концентраційна залежність величини флуктуаційного вільного об’єму (1, 2) і його відносної частки (3, 4) композицій ПВХ+Fe₃O₄ (1, 3) і ПВХ+W (2, 4).

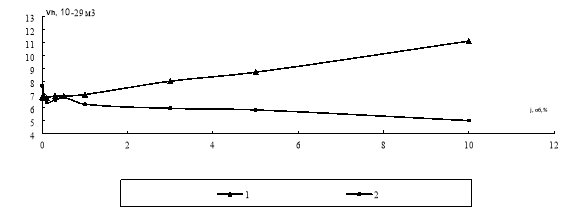
Рис. 2.2. Концентраційні залежності об’єму флуктуаційної «дірки» композицій ПВХ+Fe₃O₄ (1) і ПВХ+W (2).

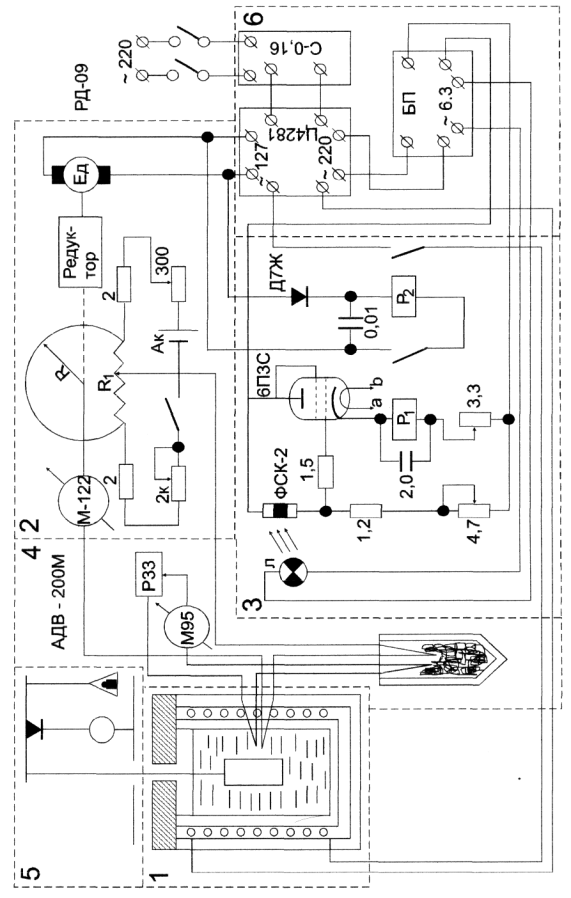
Експериментальні дослідження температурної залежності густини і кое­фіцієнтів об’ємного теплового розширення ПВХ-композицій в широкій об­ла­сті зміни температур проводились за допомогою установки (додаток 1), яка забез­печує лінійну швидкість нагрівання зразка.

Основними конструктивними елементами установки є термоблок 1, дат­чик лінійного нагріву 2, регулятор температури 3, блок вимірювання темпе­рату­ри 4, вимірювальний пристрій 4, стабілізований блок живлення. Принцип роботи ґрунтується на методі гідростатичного зважування.

Густину зразка знаходили за результатами його зважування в повітрі та імерсійній рідині і розраховували за співвідношенням:

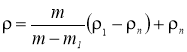,                                      (2.1)

де m, m₁ – маса зразка у повітрі і рідині, ₁, _п – густини рідини і повітря.

Коефіцієнт об’ємного розширення обчислювали за співвідношенням

 

 

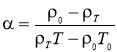,                                            (2.2)

де – відповідно густина і температура досліджуваного тіла на початку ви­мірювань; – аналогічні величини у відповідній точці температурного ін­тервалу.

Як імерсійну рідину використовували силіконове масло ПФМС–4, тем­пера­турна залежність густини якого визначалась за плавленим кварцем. Віднос­на похибка методу складає 0,3%.

Швидкість нагріву зразка контролювалась за допомогою регулятора тем­ператур і становила 2–3 К/хв. Вимірювання проводились спочатку в режимі на­грівання, а потім – в режимі охолодження.

Дослідження механічних динамічних характеристик ПКМ пов’язане з ви­мірюванням швидкостей поширення поздовжньої () та поперечної (_t) уль­тразвукових хвиль та відповідних коефіцієнтів їх затухання (_l, _t) .

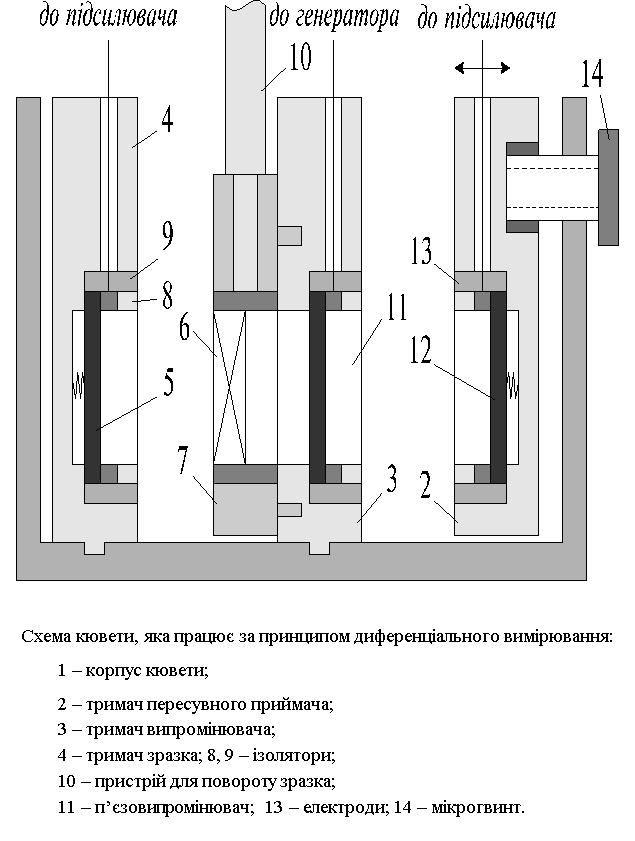
Кювета (додаток 2) містить два п’єзоприймачі, між якими в строго фік­со­ваному положенні знаходиться п’єзовипромінювач ультразвукових коливань. Передаючим середовищем є силіконове масло марки ПФМС–4, яке забез­пе­чує можливість дослідження фізико-механічних властивостей ПВБ- та ПВХ-мате­ріалів в області температур 293  473 К. В кюветі (1), яка зроблена з нержавіючої сталі, кріпляться нерухомо в тримачах (3,9) за допомогою ізоляційних прокладок (7,8) і електродів (11), випромінювач (12) і приймач (5), які при необхідності можна знімати. Дру­гий приймач (13), закріплений в тримачі (2) за допомогою мікрометричного гвинта (14), може здійснювати зворотньопоступальний рух в площині, яка перпендикулярна площині приймача і випромінювача. До тримача випро­мі­нювача (3) спеціальним пристроєм (4), який можна знімати, кріпиться дослі­джуваний зразок (6), при повороті якого навколо осі (10), що перпен­дику­лярна до напрямку поширення ультразвукової хвилі, збуджуються поздовжні та поперечні коливання.

У випадку, коли кут падіння хвилі на зразок зі строго паралельними поверхнями дорівнює нулю, в ньому буде поширюватись тільки поздовжня хвиля. При збільшенні кута повороту зразка досягається критичний кут (кут Брюстера), при якому падаюча поздовжня хвиля повністю відбивається і у зразку поширюється тільки поперечна хвиля. Дана методика дозволяє знайти кут Брюстера в залежності від релаксаційного стану і типу досліджуваного матеріалу з точністю від 0,5 до 1%.

 

2.2. Дослідження впливу силових полів на параметри вільного об’єму ПВХ-композитів

 

Як відомо, прикладання силових полів у процесі формування полімерних композицій здатне суттєво впливати на комплекс їх властивостей. Очевидно, що цей вплив визначається сумарним ефектом дії поля як на полімерну матрицю, так і на наповнювач.

На рис. 2.3, 2.4 представлені порівняльні концентраційні залежності відповідно величини вільного об’єму та його відносної частки для полівінілхлоридних композицій з феримагнітним дисперсним наповнювачем Fe₃O₄, сформованими при дії постійного магнітного поля та за його відсутності.

Рис. 2.3. Концентраційна залежність величини флуктуаційного вільного об’єму композицій ПВХ+Fe₃O₄.

 

Рис. 2.4. Концентраційна залежність частки флуаційного вільного об’єму композицій ПВХ+Fe₃O₄.

 

Як видно з отриманих даних, залежності та для відповідних ПВХ-систем мають подібний характер. Тут чітко прослідковуються області швидкої зміни величин і , які відповідають діапазонам наповнення 0÷1 та 5÷10 об.% Fe₃O₄. При вмісті оксиду заліза 1÷5 об.% зміни параметрів вільного об’єму є незначними. Характерно, що величина вільного об’єму та його відносна частка збільшуються в усій області концентрацій для композицій обох типів. Така їх поведінка може бути пояснена процесами структуроутворення, які відбуваються в граничних шарах. Густина систем ПВХ+Fe₃O₄ по мірі збільшення об’ємного вмісту наповнювача зростає, причому залежності для систем обох типів лежать нижче прямої адитивності, а величина

,

де – густини композицій, сформованих без дії магнітного поля (БП) і за його наявності (МП) для відповідних концентрацій.

Разом з тим у даних системах при збільшенні вмісту наповнювача спостерігається зменшення густини та ефективної товщини граничного шару при загальному збільшенні його об’ємного вмісту. Таким чином, в даному випадку процес структуроутворення характеризується зростання частки зон розрихлення в області граничних шарів, що і призводить до збільшення параметрів вільного об’єму.

Слід відмітити той факт, що в інтервалі концентрацій до 5 об.% параметри вільного об’єму композицій, сформованих під дією МП, більші відповідних величин для систем, які не підлягали силовій дії у процесі формування. При подальшому зростанні вмісту наповнювача спостерігається протилежна тенденція. Характерно, що аналогічна закономірність спостерігається і в концентраційній залежності густини граничного шару. Звідси можна зробити висновок, що дія магнітного поля приводить до впорядкування структури матеріалів у напрямі її компактизації.

Вплив електричного поля, прикладеного в процесі формування структури полімерних систем, на характеристики флуктуаційного вільного об’єму досліджували на прикладі систем ПВХ+W. Концентраційні залежності величин V_f, f а також об’єму «дірок» для вказаних композицій представлені на рис. 2.5, 2.6.

Для металонаповнених ПВХ-систем залежності V_f(ϕ) та f(ϕ) мають подібний характер. У випадку відсутності електричного поля до 0,5 об.% вольфраму спостерігається зростання значень V_f і f. Це можна пояснити структурними змінами, які відбуваються в композиціях під впливом високодисперсного металічного наповнювача. З точки зору трьохкомпонентної моделі наповненого полімера при малих концентраціях наповнювача (до 1 об.%) в системах на основі ПВХ відбувається інтенсивне формування граничного шару, яке супроводжується найбільш інтенсивною зміною його розмірів. при цьому великим значенням ефективної товщини міжфазного шару відповідають низькі значення його густини. В результаті структура полімерної композиції при малому вмісті наповнювача характеризується великим вільним об’ємом. При цьому, як видно з рис. 2.5, в околі концентрації наповнювача 0,5 об.% спостерігається максимум величини об’єму флуктуаційної «дірки». Це свідчить про те, що при малих концентраціях вольфраму зростання величини вільного об’єму визначається збільшенням локальних областей розрихлення у граничних шарах полімерної композиції.

Рис. 2.5. Концентраційні залежності величини флуктуаційного вільного об’єму композицій ПВХ+W.

 

Рис. 2.6. Концентраційні залежності відносної частки флуктуаційного вільного об’єму композицій ПВХ+W.

 

При подальшому збільшенні вмісту наповнювача зростає число макромолекул полімера, що переходять в граничний шар. Цей процес супроводжується зменшенням об’єму (рис. 2.5). Іншими словами, зменшення вільного об’єму металонаповнених ПВХ-композитів при об.% W обумовлене зменшенням як величини флуктуаційних «дірок», так і їх концентрації.

Аналіз концентраційних залежностей параметрів вільного об’єму композицій ПВХ+W свідчить про те, що прикладання в процесі формування структури електричного поля суттєво впливає на ці параметри.

Якщо для «чистого» ПВХ вплив електричного поля є незначним, то по мірі зростання вмісту вольфраму силова дія стає більш суттєвою. До 4 об.% W концентраційні залежності величини і відносної частки флуктуаційного вільного об’єму композицій, сформованих за наявності електричного поля, лежать нижче аналогічних залежностей систем, які не піддавалися силовій дії. При концентраціях наповнювача понад 4 об.% спостерігається протилежна тенденція. Слід відмітити, що для електричне поле практично не змінює величини вільного об’єму. В той же час залежність для композицій, сформованих в ЕП, монотонно зростає (за винятком незначного зменшення при 3 W). Якщо ж взяти до уваги і загальну тенденцію до зменшення об’єму флуктуаційної дірки V_h, то можна зробити висновок, що процеси структурної організації під дією електричного поля в металонаповнених полімерних системах супроводжуються двома конкуруючими факторами: підвищенням концентрації «дірок» і зменшенням їх величини (з домінуванням останнього процесу).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 

 Результати проведених досліджень дають можливість сформулювати наступні загальні висновки стосовно проблемних питань, що розглядаються в роботі:

1. На основі молекулярно-кінетичного підходу до високомолекулярних сполук із застосуванням модельних представлень проведено розрахунки параметрів вільного об’єму композицій на основі полівінілхлориду.
2. Показано, що величина і відносна частка флуктуаційного вільного об’єму композицій залежать від ступеня наповнення і властивостей інгредієнтів, причому ці залежності носять складний характер, що визначається специфікою взаємодій структурних елементів.
3. Досліджено вплив зовнішніх постійних електричного та магнітного полів на поведінку параметрів вільного об’єму ПВХ-систем.
4. Абсолютні значення відносної частки флуктуаційного вільного об’єму можуть характеризувати термодинамічну неврівноваженість структури полімерної системи.

 

ЛІТЕРАТУРА

 

1. Козлов Г.В., Новиков В.У. Кластерная модель аморфного состоянияполимеров // УФН. – 2001. – Т. 171. – № 7. – С. 717– 764.
2. Бордюк М.А Вплив температурного поля і наповнювачів на флуктуаційний вільний об’єм композицій на основі полівінілхлориду // Фізика конденсованих високомолекулярних систем. Наукові записки Рівненського педінституту. – 1997. – Вип. 3. – С. 21–24.
3. Бордюк М.А Флуктуаційний вільний об’єм і внутрішній тиск полівінілхлоридних композицій // Фізика конденсованих високомолекулярних систем. Наукові записки Рівненського педінституту. – 1998. – Вип. 4. – С. 3–5.
4. Колупаев Б.С., Липатов Ю.С. // Высокомолекулярныесоединения. – А. – 1986. – Т. 28. – № 8. – С. 1706–1711.
5. Сідлецький В.О. Взаємозв’язок фізико-механічних і теплофізичних властивостей гетерогенних систем на основі лінійних полімерів: Дис. ... канд. фіз-мат. наук: 01.04.19. – Рівне, 1998. – 145 с.
6. Липатов Ю.С., Привалко В.П. О связисвободногообъема с молекулярными параметрами линейныхполимеров // Высокомолек. соединения. А. – 1973. – Т. 15. – С. 1517–1522.
7. Иванищук С.Н., Бордюк Н.А., Липатов Ю.С., Колупаев Б.С. // Высокомолекулярныесоединения. – А. – 1990. – Т. 32. – № 6. – С. 1224–1231.
8. Физико-химиямногокомпонентныхполимерных систем. Т. 2. Полимерныесмеси и сплавы. / Подобщей ред. Ю.С. Липатова. – К.: Наукова думка, 1986. – 384 с.
9. Бордюк М.А., Колупаєв Б.С., Іваніщук С.М., Ліпатов Ю.С., Нікітчук В.І. прояви гармонійних та ангармонійних ефектів у пластифікованих полімер-полімерних системах // Фізика конденсованих високомолекулярних систем. Наукові записки РДПІ. – Рівне, 1998. – Вип. 5. – С. 12–17.
10. Демчук В.Б., Сідлецький В.О. Дослідження впливу зовнішнього магнітного поля на характер структурної взаємодії в гетерогенних полімерних системах // Фізика конденсованих високомолекулярних систем. Наукові записки Рівненського державного гуманітарного університету. – 2002. – Вип. 9. – С. 47–49.

 

11. Гудь. В.М. Застосування фрактального та мультифрактального підходів до вивчення конформаційних, механічних та теплофізичних властивостей полімерних систем. Магістерська робота. – Рівне: РДГУ, 2005. – 95 с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТКИ

Додаток 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2