Розробка конспекту уроку на тему "Вправи на всі дії з натуральними числами" для учнів 5 класу
Тема уроку: «Вправи на всі дії з натуральними числами»
Мета уроку: узагальнити та систематизувати знання учнів про натуральні числа; сформувати правило порядку виконання дій у виразах; розвивати уяву та логічне мислення при розв’язуванні задач; вдосконалювати вміння учнів виконувати вправи на всі дії з натуральними числами, використовувати властивості арифметичних дій під час розв’язування вправ різних рівнів складності; виховувати розуміння математики в житті та повсякденному житті; сприяти формуванню здорового моральному клімату в класі.
Тип уроку: систематизація умінь та знань.
Обладнання: конспект уроку, картки з завданнями.
Хід уроку
І. Організаційний момент
Привітання з учнями. Оголошення результатів контрольної роботи та аналіз контрольної роботи.
ІІ. Повідомлення теми та мети уроку
— Ви, діти, вже навчилися виконувати різні дії над виразами та задачами. Так ось сьогодні ми будемо ваші навички та знання перевіряти за допомогою різних цікавих вправ. І так тема уроку…(оголошення теми і мети уроку)
ІІІ. Актуалізація опорних знань
— Спершу ніж перейти до виконання вправ, треба нам з вами згадати, який правильний порядок дій повинен бути у нас з вами в різних математичних ситуаціях. А які це ситуації, ми з вами зараз дізнаємося.
У вас у кожного лежить листок з завданням «Знайди пару». Зверніть увагу на те, що є чотири стовпця, перші два і останній заповненні, а третій ні. Так ось, вам потрібно відповідно до перших двох стовпців розставити відповідні числа напроти останнього стовпця, потрібна нумерація у першому стовпчику. Зараз по команді ви почнете виконувати це завдання в парах, зі своїм сусідом по парті, на це вам дається 2 хвилини. Раз, два, почали. (виконання вправи)
|
Знайди пару |
|||
|
Нумерація |
Початок твердження |
Вставити відповідний номер |
Продовження твердження |
|
1 |
У виразах із дужками спочатку обчислюються |
|
можна помножити на це число кожний доданок і ці добутки додати =a∙c+b∙c. |
|
2 |
Щоб помножити суму на число (a+b)∙c= |
|
рівнянням. |
|
3 |
Нам відомо п’ять |
|
арифметичних дій: додавання, віднімання, множення, ділення і піднесення до степеня. |
|
4 |
Розв’язати рівняння означає |
|
значення виразів у дужках. |
|
5 |
Значення невідомого, при якому рівняння перетворюється на правильну числову рівність, називається |
|
розв’язком або коренем рівняння. |
|
6 |
У виразах без дужок спочатку виконуються |
|
знайти всі його корені або показати, що їх немає. |
|
7 |
Щоб помножити різницю на число (a-b)∙c= |
|
піднесення до степеня, потім по порядку зліва направо множення і ділення, а потім додавання і віднімання. |
|
8 |
Рівність, що містить невідоме, називається |
|
можна зменшуване і від’ємник помножити на це число і від першого добутку відняти другий =a∙c-b∙c. |
— А тепер по черзі хтось з пари оголошує по одному твердженню з місця.
IV. Розв’язування вправ та задач. Робота за підручником
— Тепер попрацюємо з підручником. Спочатку усні вправи, для цього відкрийте ваш підручник на сторінці 93 вправа № 543.
— Молодці. Тепер зверніть увагу на дошку, і виконаємо такі приклади теж усно, але щось з ними не так, можете мені сказати,що саме? (відповіді учнів) Так, справді вони кругові, але ж це для нас не проблема, тоді гайда їх розв’язувати.(Кругові приклади – додатки до уроку).
— А тепер давайте попрацюємо письмово: приклади № 544 виконуємо 1 і 4, і до дошки підуть одразу два учні, останні розв’язують з місця і порівнюють результати. До дошки йдуть ______________________________________


— Добре, бачу що ви пам’ятаєте, як виконувати приклади різними арифметичними діями і дужками, тому переходимо до виразів, вправа № 548 (вираз 2).

— Ускладнюємо наш урок задачами № 550, 554, 557. Ті, хто можуть розв’язати без допомоги, розв’язуйте самостійно і звіряємо з дошкою.

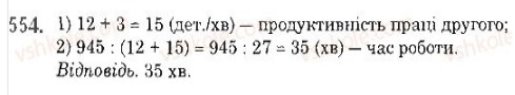

— Ми розв’язували приклади, вирази, задачі, але якийсь вид математичних виразів ми ще не розв’язували, який?(відповідь учнів) Правильно — це рівняння, тому відкриваємо сторінку 95 підручника вправа № 570.

V. Підсумок уроку
Рефлексія: — Наш урок майже добіг кінця,тому пропоную методом «Мікрофона» висловитися одним реченням про сьогоднішню нашу роботу.
VI. Домашнє завдання
1. Прочитати § 16, розглянути правила виконання дій.
2. Виконати вправи: №545, № 551, № 558.
Додаток 1
|
Знайди пару |
|||
|
Нумерація |
Початок твердження |
Вставити відповідний номер |
Продовження твердження |
|
1 |
У виразах із дужками спочатку обчислюються |
|
можна помножити на це число кожний доданок і ці добутки додати =a∙c+b∙c. |
|
2 |
Щоб помножити суму на число (a+b)∙c= |
|
рівнянням. |
|
3 |
Нам відомо п’ять |
|
розв’язком або коренем рівняння. |
|
4 |
Розв’язати рівняння означає |
|
значення виразів у дужках. |
|
5 |
Значення невідомого, при якому рівняння перетворюється на правильну числову рівність, називається |
|
арифметичних дій: додавання, віднімання, множення, ділення і піднесення до степеня. |
|
6 |
У виразах без дужок спочатку виконуються |
|
знайти всі його корені або показати, що їх немає. |
|
7 |
Щоб помножити різницю на число (a-b)∙c= |
|
піднесення до степеня, потім по порядку зліва направо множення і ділення, а потім додавання і віднімання. |
|
8 |
Рівність, що містить невідоме, називається |
|
можна зменшуване і від’ємник помножити на це число і від першого добутку відняти другий =a∙c-b∙c. |
Додаток 2
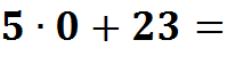
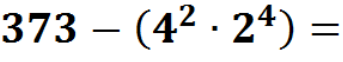
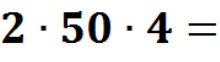

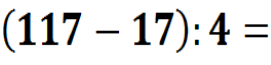
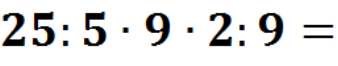
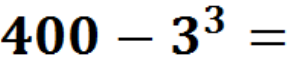
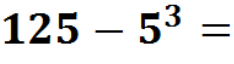
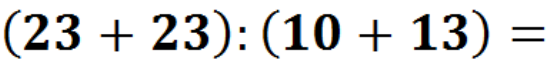
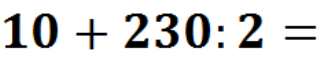


про публікацію авторської розробки
Додати розробку
