Розробка методичного прийому для організації самостійної роботи на уроках алгебри в 9-11 класах «Тридцять варіантів за три хвилини»

Скадовська спеціалізована загальноосвітня школа І-ІІІ ступенів «Академія творчості»

 

 

 

 

 

 

 

          Розробка методичного прийому для організації          самостійної   роботи   на  уроках  алгебри в  9-11 класах

 

«Тридцять варіантів за три хвилини»

 

 

                                     вчителя математики

                   спеціаліста вищої категорії

                                      вчителя методиста

                 Гавриш Світлани Петрівни

 

 

 

 

                                           Методична розробка

                             «Тридцять варіантів за три хвилини»

Приблизно стільки часу знадобиться для того, щоб забезпечити кожного учня класу окремим завданням на різнорівневій самостійній роботі, не використовуючи при цьому роздатковий матеріал.  

Суть цього прийому продемонструю на прикладі організації самостійної роботи з теми «Розв'язування нерівностей методом інтервалів»

На дошці записуються нерівності, які треба розв'язати під час самостійної роботи.

1) 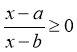;            2)

3)

Кожному учню повідомляється тризначний номер варіанту abc. Отримавши його, учень виконує підстановку в умову вправ, записаних на дошці, значення а, b, с   які відповідають цьому варіанту.

Наприклад, учень, який отримав варіант № 247, повинен в умову кожної вправи замість а підставити 2, замість в - 4, замість с - 7 і розв'язати такі нерівності:

         1) 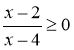            2)

         3)

Називаючи тільки такі номери аbс, у яких a<b<c, можна отримати однакові за структурою відповіді до кожної вправи. Відповіді залежать тільки від порядку розміщення на числовій прямій натуральних значень а, b, с.  Тому при умові, що а<b<с,  вони будуть мати наступний вигляд:

1)

2)

3)

Доцільно розділити клас на групи і, в залежності від знань і умінь кожної, запропонувати відповідний варіант роботи. В даному випадку для найбільш підготовлених учнів можна записати на дошці такі нерівності:

1) ;

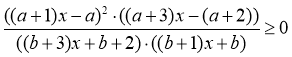2) ;

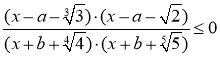3)

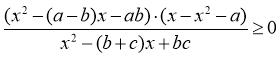
Відповіді: (при а, b, с - натуральних і а<b<с)

1)

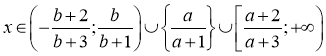
2)

3)

За допомогою такого способу можна проводити самостійні роботи по багатьом розділам курсу алгебри і початків аналізу, Однак в деяких ситуаціях зручніше користуватися таблицями. Наприклад, при проведені самостійної роботи в 10 класі з теми «Розв'язування тригонометричних рівнянь» на дошці заздалегідь записані три варіанти самостійної роботи.  Припустимо такі:

Варіант 1.    1)

                      2)

Варіант 2.    1)

                      2)

Варіант 3.

                1)

               2)

Невідомі значення констант і найменування функцій учні дізнаються із розміщених на дошці таблиць.

Таблиця 1

	а2	а3	а4	а5	а6	а7	а8	a9	a10	a11
	-1				0				1

 

Таблиця 2

(x)	(x)	(x)	(x)
sin x	cos x	tg x	сtg x

 

Якщо учень отримав на самостійній роботі  варіант 2 з індексами і=2, j=3, к=4, l=5, то він повинен розв'язати наступні рівняння:

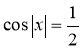
     1)                  2)

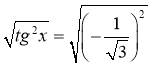
Застосування таких прийомів організації самостійних, робіт особливо ефективне на початковому етапі вивчення будь-якої теми, коли для подальшого більш глибокого опрацювання матеріалу треба бути впевненим в тому, що кожен учень оволодів необхідними для цього знаннями і успішно засвоїв алгоритми виконання найпростіших вправ.

Підготовка таких самостійних робіт не потребує великих затрат часу, дозволяє зосередити основну увагу на допомозі в подоланні певних труднощів кожною групою учнів, швидко проводити корекцію індивідуальних завдань.

Малі затрати часу при організації роботи та індивідуальність отриманих завдань дозволяють частіше проводити письмові індивідуальні опитування, роблять обернений зв'язок учнів з учителем більш стійким та інформативним, що допомагає знаходити і виправляти відхилення від бажаних результатів навчання.

Такі прийоми застосовуються при складанні навчальних і контролюючих програм для комп'ютерних класів.