Розробка "Олімпіадні завдання 8 клас"
Обласна олімпіада з математики (8 клас)
-
Розв’язати в натуральних числах рівняння:
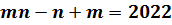
Розв’язання:
![]()
![]()
![]()
Розкладемо на прості множники 2021=43![]() 47 , маємо варіанти:
47 , маємо варіанти:
-
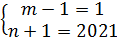 ;
; 
-
 ;
; 
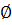
-
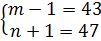 ;
; 
-
 ;
; 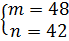
Відповідь (m;n): (2;2019) , (44;46) , (48;42)
2. Порівняйте числа ![]() і
і ![]()
Розв’язання:
Ι Спосіб. Так як ліва і права частини додатні , то піднесемо їх до квадрату. ![]() і
і ![]()
![]() і
і ![]()
![]() і 8024 (віднімемо число 4012)
і 8024 (віднімемо число 4012)
![]() і 4012 (поділимо на 2)
і 4012 (поділимо на 2)
![]() і 2006 (знову піднесемо до квадрату)
і 2006 (знову піднесемо до квадрату)
![]() і
і ![]()
4024035 < 4024036
Значить: ![]() <
< ![]()
ΙΙ Спосіб. Помножимо чисельник і знаменник в лівій і правій частинах на одне і теж число.
![]()
![]()
![]()
![]()
2 2·![]()
1 < ![]()
Порівняємо ![]() ;
; ![]() >
> ![]() , бо 2007 більше ніж 2005 , тоді число
, бо 2007 більше ніж 2005 , тоді число ![]() >1.
>1.
3. Песик Гав може з’їсти батон докторської ковбаси за 1 хвилину, а батон любительської ковбаси за 2 хвилини. Кицька Няв може з’їсти батон докторської ковбаси за 2 хвилини, а батон любительської ковбаси за 3 хвилини. Кожен батон ковбаси вони можуть їсти одночасно з протилежних боків. За який найменший час вони разом можуть з’їсти два батони ковбаси, один з яких – докторська, а другий – любительська?
Розв’язання:
Їдять батони одночасно без перерви. Нехай довжина докторської ковбаси =S, а любительської = L. Тоді знайдемо швидкість поїдання ковбаси Гавом (![]() ) і Нявом (
) і Нявом (![]() ).
). ![]()
![]()
Нехай Гав з’їв частину ![]() докторської і частину
докторської і частину ![]() любительської ковбаси, тоді Няв відповідно з’їв
любительської ковбаси, тоді Няв відповідно з’їв ![]() і
і ![]() . За умовою час з’їдання ковбас рівний. Тоді
. За умовою час з’їдання ковбас рівний. Тоді  - час поїдання ковбаси Гавом, і
- час поїдання ковбаси Гавом, і  -
-
час поїдання ковбаси кицькою Няв. Порівняємо ці величини і врахуємо, що час повинен бути найменшим. Позначимо ![]() , а
, а ![]() , зрозуміло, що ці дві невідомі величини належать проміжку
, зрозуміло, що ці дві невідомі величини належать проміжку ![]() . Отже маємо:
. Отже маємо:
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() . Час поїдання ковбаси у персонажів рівний і повинен бути найменшим, тобто
. Час поїдання ковбаси у персонажів рівний і повинен бути найменшим, тобто ![]() (це час поїдання
(це час поїдання
ковбаси Гавом) і цей час повинен бути найменшим, отже
![]() - найменше, тоді
- найменше, тоді ![]() ,
, ![]() , значить
, значить ![]() . Відповідь:
. Відповідь:![]() хв.
хв.
4. Ціле число а має властивість: число 3а можна подати у вигляді ![]() , де
, де ![]() і
і ![]() цілі числа. Доведіть, що і число а можна подати у такому самому вигляді.
цілі числа. Доведіть, що і число а можна подати у такому самому вигляді.
Розв’язання:
![]() , ліва частина ділиться на 3, отже і права теж ділиться на 3.
, ліва частина ділиться на 3, отже і права теж ділиться на 3.
Так як ![]() ділиться на 3, то і
ділиться на 3, то і ![]() теж ділиться на 3, а отже і х ділиться на 3, тоді
теж ділиться на 3, а отже і х ділиться на 3, тоді ![]() . Маємо
. Маємо ![]() ;
; ![]() ;
; ![]() . Число а можна подати у такому самому вигляді як і 3а.
. Число а можна подати у такому самому вигляді як і 3а.
5. Обчислити суму ![]() , якщо відомо, що
, якщо відомо, що ![]() .
.
Розв’язання:
![]() =
= ![]() =
= ![]() =
=![]() =1.
=1.
Відповідь:1.
6. Розв’яжіть систему рівнянь 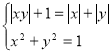
Розв’язання:
1) Нехай ![]() , тоді
, тоді 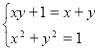 ;
;  ;
; 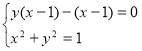 ;
; 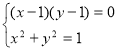 ;
; ![]() або
або ![]() .
.
2) нехай ![]() , тоді
, тоді  ;
;  ;
; 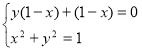 ;
;
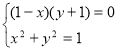 ;
; ![]() або
або ![]() Обидва розв’язки не задовольняють.
Обидва розв’язки не задовольняють.
3) нехай ![]() , тоді
, тоді  ;
; 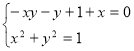 ;
;  ;
;
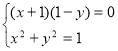 ;
; ![]() або
або ![]() Обидва розв’язки не задовольняють.
Обидва розв’язки не задовольняють.
4) Нехай ![]() ,
,  ;
; 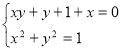 ;
; 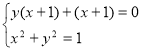 ;
;

![]() або
або ![]()
![]()
![]()
Відповідь: (1;0) ; (-1;0) ; (0;1) ; (0;-1).


про публікацію авторської розробки
Додати розробку
