Розробка уроку алгебри для учнів 11 класу на тему "Теорія ймовірностей. Випадкові події"

Алгебра

11 клас

Тема: Теорія ймовірностей. Випадкові події

Мета:

• навчальна:

•              систематизувати та поглибити знання учнів про основні поняття теорії ймовірностей, отримані в 6 та 9 класах;

• розвиваюча:

•              розвивати увагу, мислення, культуру математичного мовлення;
•              вміння працювати самостійно, аналізувати ситуацію,
  розвивати загально навчальні навички ;
•              сприяти розвитку комунікативної, інформаційної, соціальної компетентностей, а також самоосвіти і саморозвитку, продуктивної творчої діяльності;

• виховні:

•              виховувати уважність, кмітливість, самостійність

Тип уроку: комбінований

Обладнання: ПК, проектор, МД, презентація MS PowerPoint, опорний конспект

Попередня підготовка:

Завдання для:

• дослідників: І учень проводить дослід щодо появи «герба» чи «числа» при підкиданні монети; ІІ учень готує  інформацію про результати аналогічних дослідів в історії математики;
• статистиків: два учні пропонують бажаючим (учням інших класів, вчителям) прийняти участь у наступному екстерименті.

Кожен пише на аркуші паперу будь-які чотири слова. Після цього підраховує, скільки букв у кожному з написаних слів, і записує числа проти відповідного слова. Після цього кількість парних чисел записується в рамочку.

Статистики підраховують кількість аркушів з числом 0,1,2,3,4. Результати доповнюють на уроці та оформлюють у вигляді таблиці.

• «фокусника-іллюзіониста»: підготуватися до «передбачення» можливого розподілу результатів експерименту.

1. Всі чотири слова можуть мати парне число букв в 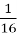частині всіх аркушів.
2. Три слова можуть мати парне число букв в 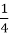частині всіх аркушів.
3. Два слова можуть мати парне число букв в 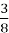частині всіх аркушів.
4. Одне слово може мати парне число букв в 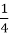частині всіх аркушів.
5. Жодного слова з парним числом букв може не бути  в 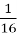частині всіх аркушів.

Хід уроку

Девіз:

Мати можливість вибирати – це свобода.

Усвідомлений та обґрунтований вибір – це успіх та свобода.

1. Організаційна частина
2. Повідомлення теми,  мотивація навчальної діяльності:

Зараз ми з вами проведемо лотерею. Подивіться уважно на свої робочі місця. На парті у кожного з вас знаходиться картка з номером. Хто наймолодший учень вашого класу? Витягни з мішечка картку з номером. Номер №_

У кого такий номер? Сьогодні тобі пощастило. Ти отримаєш приз.

Чи сподівались ви, що сьогодняшній урок почнеться саме так?

Подія, яка відбулась зараз, була для вас неочікуваною?

У житті з нами відбуваються різні події: приємні і неприємні, очікувані і неочікувані, випадкові.

Характерною особливістю математики, яку ви до сих пір вивчали в школи, є визначеність невідомих, що знаходилися під час розв’язування різноманітних задач. Наприклад, 2*8=18, а об’єм куба з ребром 3см дорівнює 27см³.

Але в житті доводиться мати справу з подіями реального світу, що залежать від обставин, які або невідомі, або не піддаються обліку.

Події такого характеру називають випадковими. Теорія ймовірностей займається вивченням випадкових подій.

3. Систематизація та поглиблення знань, формування вмінь

У природі немає жодного фізичного явища, в якому б не мали місце елементи випадковості. Але в масових випадкових подіях існують закономірності, які піддаються обліку.

Разом з масовими випадковими подіями існують і одиничні випадкові події, наприклад падіння Тунгуського метеорита.

Теорія ймовірності вивчає лише масові випадкові події.

Розглянемо приклади, які підтверджують існування закономірностей в масових випадкових подіях.

Приклад 1. Вивчення закономірностей появи «герба» чи «числа» при підкиданні монети.

Виступ дослідників із результатами досліду та інформацією про результати аналогічних дослідів в історії математики

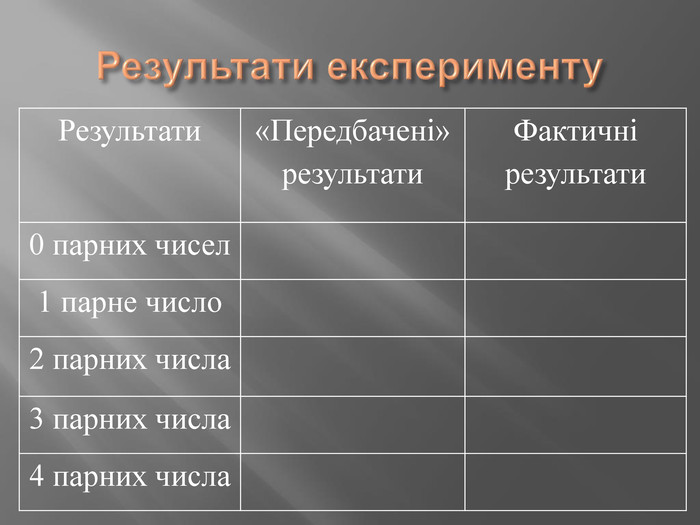
Приклад 2. Кожен учень класу пише на аркуші паперу будь-які чотири слова. Після цього підраховує, скільки букв у кожному з написаних слів, і записує числа проти відповідного слова. Після цього кількість парних чисел записується в рамочку. Дослідимо закономірності появи у рамочці чисел 0,1,2,3,4.

Фокусник-іллюзіонист: за загальним числом учасників «передбачає» результати

Статистик: підраховує кількість аркушів з числом 0,1,2,3,4. (результат - таблиця)

Результати	«Передбачені» результати	Фактичні результати
0 парних чисел
1 парне число
2 парних числа
3 парних числа
4 парних числа

 Результати досліду

• Як бачимо, ще до проведення досліду виявилося можливим теоретичними міркуваннями передбачити його результати з невеликою похибкою. Уміння передбачити хід досліду, і якому присутні елементи випадковості, дає можливість впливати на його результати. Прикладом такого передбачення може бути історія азартних ігор, які були вже поширені вже в XVII ст. Вважають, що саме з однієї з них  - гри в кості – розпочалася наука про випадкове.

Історична довідка:

Задачі, які можуть бути віднесені до теорії ймовірностей, ставилися ще у глибоку давнину. Вони розв’язувалися на примітивному рівні, адже спеціальних методів у той час ще не було. Йшло накопичення матеріалу.

Цей період кінчається в XVI ст. роботами Кардано, Пачолі, Тарталья й ін. Ці вчені під час дослідження азартних ігор виявили деякі властивості випадкових подій.

Д. Кардано (1501–1576 р.) у своїй роботі «Книга про гру в кості» впритул підійшов до визначення поняття ймовірності через відношення рівноможливих подій.

У роботах Л. Пачоли, Н. Тарталья робиться спроба виділити нове поняття ймовірності – відношення шансів – при рішенні ряду специфічних задач, насамперед комбінаторних.

Досліджуючи прогнозування виграшу в азартних іграх, Блез Паскаль і П'єр Ферма відкрили перші ймовірнісні закономірності, що виникають при киданні костей .

Вважають, що вперше Паскаль зайнявся теорією ймовірностей під впливом питань,поставлених перед ним одним з придворних французького двору Шевальє де Мере (1607-1648), що був азартним гравцем.

Справжню наукову основу теорії ймовірностей заклав великий математик Якоб Бернуллі (1654-1705).

Сучасний вигляд теорія ймовірностей отримала завдяки аксіоматизації, запропонованої Андрієм Миколайовичем Колмогоровим (1903-1987). У результаті теорія ймовірностей придбала строгий математичний вигляд і остаточно стала сприйматися як один з розділів математики.

Українська математична наука подарувала світові плеяду видатних фахівців у галузі теорії ймовірностей. Імена Й.І.Гіхмана, Б.В.Гнеденка, А.В.Скорохода, М.Й.Ядренка відомі математикам у всьому світі.

Сучасне природознавство широко користується теорією ймовірностей як теоретичною основою для обробки результатів спостережень у фізиці, механіці, астрономії, біології. Теорія ймовірностей знаходить застосування в економіці, статистиці, військовій справі. Теорію ймовірностей використовується навіть у гуманітарних науках, зокрема в історичних дослідженнях, в археології для розшифровування написів мовами давно зниклих народів, у шифруванні та дешифруванні, у вивченні закономірностей літературної мови письменників та поетів.

Всі події можна розділити на вірогідні, неможливі та випадкові.

Вірогідна подія – це та подія, яка обов’язково відбудеться за будь-якого наслідку досліду.

Неможлива подія – це подія, яка ніколи не відбудеться в заданому досліді.

Випадкова подія – це та подія в заданому досліді, яка може відбутися або не відбутися. (опорний конспект)

Завдання 1:

Які з наступних подій — випадкові, вірогідні, неможливі:

а) черепаха навчиться говорити;

б) вода, що в каструлі, яка стоїть на гарячій плиті, закипить;

в) твій день народження — 2 лютого;

г) день народження твого товариша — 20 березня;

д) твій тато, взявши участь у лотереї, виграє;

є) ти не виграєш, беручи участь у безпрограшній лотереї;

ж) ти програєш партію в шахи;

з) на наступному тижні погода буде дощовою;

и) ти натиснув на кнопку дверного дзвінка, а звук не пролунав;

к) після четверга буде п'ятниця;

л) після п'ятниці буде неділя.

Дві події А і В називаються несумісними,якщо поява однієї із них виключає появу іншої в даному досліді, в іншому разі події сумісні.

Дві події А і В називаються рівноможливими, якщо при виконанні досліду однаково можливі появи подій А і В.

Повною групою подій називається множина таких подій, що в результаті випробування повинна відбутися хоча б одна з них.

Сукупність несумісних рівноможливих подій, які утворюють повну групу, називають простором або множиною елементарних подій, події при цьому називають елементарними. (опорний конспект)

Завдання 2. Складіть простір елементарних подій за одноразового підкидання двох монет.

Завдання 3. В одній скриньці – біла, синя і чорна кульки, а в іншій – біла і синя кульки. Із кожної скриньки навмання беруть по одній кульці. Складіть простір елементарних подій.

4. Підсумок уроку:

У повсякденному житті кожній людині доводиться мати справу з різними проявами випадковостей, адже навколишній світ на­повнений подіями, багато з яких мають по декілька можливих наслідків.

Людина змушена приймати безліч рішень. Зрозуміло, що обґрунтований і прогнозований вибір є кращим, ніж вибір навмання, оскільки передбачити наслідки певних дій — це можливість прийняття оптимального рішення, уникнення незапланованих витрат, досягнення бажаного результату.

Про випадкові події навіть складають вірши.

Александр Александрович Блок

Жизнь - без начала и конца.
Нас всех подстерегает случай.
Над нами - сумрак неминучий,
Иль ясность божьего лица.

Рефлексія

Cьогодні я довідався про…

• було цікаво...
• я зрозумів, що...
• тепер я можу...
• мене здивувало...

5. Домашнє завдання:

1. опрацювати опорний конспект;
2. Складіть простір елементарних подій:

• при киданні грального кубика;
• при двох пострілах по мішені;
• у скриньці є біла, жовта, синя і чорна кульки. Беруть дві з них.