Розробка уроку геометрії "Синус, косинус, тангенс гострого кута прямокутного трикутника"

Урок №37

Тема: Синус, косинус, тангенс гострого кута прямокутного трикутника

 

Мета:

Формавання предметних компетентностей:

• сформувати поняття синуса, косинуса, тангенса гострого кута прямокутного трикутника;
• сформквати вміння застосовувати ці поняття до розв’язування задач.

Формування ключових компетентностей:

• формувати вміння доречно та коректно вживати в мовленні математичну термінрологію;
• сприяти усвідомленню важливості вивчення іноземних мов для розуміння математичних термінів та позначень;
• сприяти самовихованню творчої активності, зацікавленості в пізнанні нового.

 

Тип уроку: засвоєння ногвих знань та вмінь

 

Обладнання та наочність: презентація, роздатковий матеріал.

 

Хід уроку:

 

І. Організаційний етап

 

ІІ. Перевірка домашнього завдання

 

ІІІ. Мотивація

 

Подивіться на картинки і подумайте, що спільне їх об’єднує?

( кардиограма, маятник, риба, дах кінотеатру ....)

Іх об’єднує розділ математики, який має назву «Тригонометрія». Більш  детальніше про це поговоримо наприкінці уроку.

 

А зараз дізнаємося, що це за наука – тригонометрія.

Тригонометрія у перекладі з грецької означає «вимірювання трикурників» Тригонометрія (від грец. trigwnon - трикутник  и  metrew - виміряю)

Тригонометрія виникла із практичних потреб людини.

 

Історики вважають, що тригонометрію створили стародавні астрономи.

За допомогою співвідношень між кутами та сторонами у прямокутному трикутнику вони вимірювали відстань між планетами та зірками.

 

Трохи пізніше її почали використовувати в мореплавстві й архітектурі.

Давні люди за допомогою зірок визначали місце знаходження кораблів у морі.

 

Обчислювали висоту дерева, порівнюючи довжину його тіні з довжиною тіні від шеста, висота якого була відома.

 

За допомогою співвідношень між кутами та сторонами прямокутного трикутника люди вимірювали висоту споруд.

 

З часом сфера застосування тригонометрії постійно розширювалась, в теперішній час її використовують майже всі природничі науки, техніка і низка інших галузей діяльності людини.

 

Сьогодні на уроці ми познайомимося із її геометричними аспектами.

 

Тож запишемо тему уроку: Синус, косинус, тангенс гострого кута прямокутного трикутника.

 

ІV. Актуалізація опорних знань.

 

1. Який трикутник називають прямокутним?
2. Як називаються сторони у прямокутному трикутнику?
3. Що таке катети?
4. Що таке гіпотенуза?
5. Порівняйте їх.
6. Сформулюйте теорему Піфагора.

Робота з малюнками.

1. Назвіть катет, протилежний (прилеглий)до певного кута.
2. Запишіть відношення протилежного катета до гіпотенузи.
3. Запишіть відношення прилеглого катета до гіпотенузи.

 

V.Засвоєння нових знань.

 

Розглянемо прямокутний трикутник АВС. ( кут С = 90⁰)

 

Запишіть відношення протилежного катета до гіпотенузи та допишіть перед ним слово Sin А .

 

Sin А=ВС/АВ

 

А налогічно із косинусом та тангенсом.

 

Сформулюємо правила колективно.

 

 

 

 

 

Означення.

1. Синусом гострого кута прямокутного трикутника називають відношення протилежного катета до гіпотенузи.

 

Sin А=ВС/АВ

 

Історична довідка.

 

Індійськіські математики слово синус записали як «джива».

Арабські математики переводити з індійської мови не захотіли і записав його по буквам «д-ж-и-в-а». Потім подумали: «Що тут написано? «Джиба»? Мабуть «Джайб»?» «Джайб» - це пазуха.

Європейські математики слово пазуха перевели на латинь як синус (впадина, кривизна».

Помилку помітили лине в 19 сторіччі, але міняти нічого не стали. Адже це нікому не заважало.

 

Означення.

2. Косинусом гострого кута прямокутного трикутника називають відношення протилежного катета до гіпотенузи.

 

Cos А = АС/АВ

 

Довідка. Косинус – від латинського «компліментарі синус» - додатковий синус.

 

Означення.

3. Тангенсом гострого кута прямокутного трикутника називають відношення протилежного катета до прилеглого.

 

Tg А = ВС/АС

 

Тангенс – у перекладі з латинської «дотичний»

 

Означення.

Котангенсом гострого кута прямокутного трикутника називають відношення прилеглого катета до протилежного

 

Запишіть дані співвідношення для гострого кута В.

 

VI. Застосування отриманих знань.

Завдання (усно)

Розглянемо прямокутні трикутники.

Визначте синус, косинус, тангенс для гострих кутів даних прямокутних трикутників.

 

Задачі на  побудову гострого кута прямокутного трикутника за його синусом, совинусом та тангенсом.

 

Відеоурок.

Практичне завдання. Побудуйте кута синус якого 3/5,  та кут тангенс якого 5/4.

Фіскультхвилинка

 

Розмірковуємо!

1. Чи правильна нерівність sinα > 1? Відповідь пояснити.

2. Чи правильна нерівність cosα > 1? Відповідь пояснити.

3. Чи правильна нерівність tgα > 1? Відповідь пояснити.

Висновок

Значення sinα , cosα  не може бути більше одиниці, тому, що катет завжди менший від гіпотенузи.

Значення tgα , сtgα може бути більше одиниці і менше одиниці, тому, що катети можуть бути і менше і більше один одного.

 

Розв'язування письмових задач.

 

Задача 1.. Знайдіть синус, косинус, тангенс найменшого кута єгипетського трикутника.

 

 

Задача 2.

 

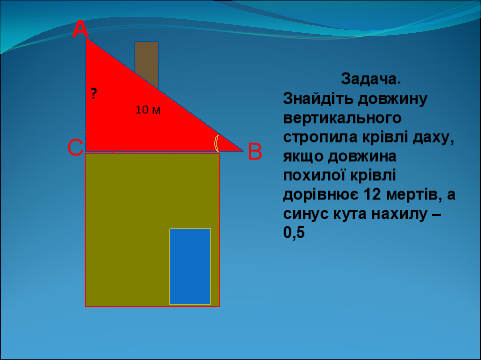
Задача 3. (№ 668)

Катети прямокутного трикутника допівнюють 8см і 15 см. Обчисліть синус, косинус і тангенс найменшого кута трикутника.

Задача 4. У прямокутному трикутнику АВС ( кут С = 90⁰) катет а=5 см, гіпотенуза с = 13 см. Знайдіть синус, косинус, тангенс кута В.

 

 Задача 5. У прямокутному трикутнику гіпотенуза дорівнює 13 см, а косинус одного з гострих кутів дорівнює — 5/13. Знайдіть катети трикутника.

 

Підсумок уроку. Рефлексія.

 

Повернемося до того, з чого ми розпочали свій урок.

Як же пов'язані зображення?

 

Домашнє завдання

Опрацювати параграф 19.1

Розв'язати

№665 (середній рівень)

№ 667 (достатній рівень)

№676 (високий рівень)