​Розробка уроку математики в 10 класі.

Розробка уроку математики в 10 класі.

 

Тема: Нестандартні способи розв’язання ірраціональних рівнянь.

Мета: Систематизувати знання учнів про ірраціональні рівняння,

           познайомити з новими способами їх розв’язання , розвивати

           культуру математичного мислення, виховувати інтерес до

           інтелектуальної праці.

Тип:  Урок-семінар.

Обладнання: Схеми, опорні конспекти.

 

Епіграф: Знання лише тоді є знаннями, коли вони здобуті зусиллями

                своєї думки, а не пам’яттю.

                                                                                  Л. Толстой.

 

Зміст уроку.

І. Актуалізація опорних знань.

  1.Перевірка виконання учнями домашнього завдання (усно).

  2.Запитання до класу (фронтальне опитування):

     1.Які рівняння називаються ірраціональними?

     2.Які з наведених рівнянь не є ірраціональними?

        а) 2х+х²+ 12=0;            б)  + х=0 ;

        в) х³+ - -11=0;         г) 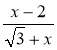   -х⁴=0.

    3.Що таке ОДЗ ірраціонального рівняння?

    4.Яка дія є обов’язковою під час розв’язання ірраціонального

       рівняння?

    5.Знайти ОДЗ рівнянь:

      а) =1   ( ) ;           б)   + 3=0   () ;

      в) + =0  () ;  г)   5- =0  ( (5; ) ).

   6.Які способи розв’язання ірраціональних рівнянь ви знаєте?

   7.Яким способом можна розв’язати  наведені рівняння?

      а) -  =1 ;                  б) +   =0 ;

      в) -3=4 .

   8.Чому рівняння = - 5, не має розв’язків?

   9.Які перетворення ірраціональних рівнянь можуть призвести до

      появи сторонніх коренів?

   10.Чи обов’язково вказувати ОДЗ при розв’язанні ірраціональних

        рівнянь, якщо ні, то як виключають сторонні розв’язки?

 

ІІ. Ознайомлення учнів з іншими способами розв’язування ірраціональних рівнянь, які не розглядаються в шкільному курсі алгебри. Виступи експертів.

 

 1 експерт. Спосіб зведення ірраціонального рівняння до системи

    раціональних рівнянь. Розглядаємо на прикладах, з поясненням.

 Приклад 1. -=0 , нехай =а , а =в, тоді х+1=а³, і

  х-3=в², звідси складемо систему раціональних рівнянь:

     

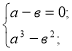
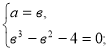
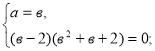
  з системи маємо рівняння в²+в+2=0 коренів не має, а в=2, а=2,

  =2, х+1=8, х=7.

  Перевірка показує , що корінь х=7 задовольняє умову.

  Відповідь: 7.

 

 Алгоритм : 1.Введення нової змінної.

                     2.Складаємо систему раціональних рівнянь з новими

                        змінними.

                     3.Розвязуємо її.

                     4.Знайдене значення однієї змінної підставляємо в

                        вираз яким її позначено.

                     5.Розвязуємо утворене рівняння.

 

 Приклад 2.   + = 11,  нехай  =а, =в, тоді 

     х+7=а², х-4=в², маємо:

              

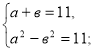
    звідси 2а=12,  а=6,  тоді =6, х+7=36 , х=29.

    Перевірка:  +  = 11.

    Відповідь: 29.

 

2 експерт. Спосіб виділення повного квадрата. Використовують в таких ірраціональних рівняннях, в яких підкореневий вираз можна подати у вигляді повного квадрата. Розглянемо на прикладах.

 

 Приклад 1.  - =1 ,   ОДЗ: х 2,

    -   = 1,

       -   = 1,        +1 0,          

     Розглянемо при яких х   -1 =0,  =1,  х-2=1,  х=3, звідси:

    а) х 3  :     +1- +1=0,   2 1 , розв’язків немає.

    б) 2х3  :   +1+ -1= 1,   2=1,  =0,5,  х-2=0,25,

                       х=2,25.

    Перевірка:

    Відповідь: 2,25

 

   Приклад 2.    + =3  ,    ОДЗ: х 1,

    + =3,     +=3,

       Розглянемо -1=0,   х-1=1,  х=2,

       а) при   1х<2  :  (+1) – (  -1)=3,   23 ,

       б) при х2  :  + -1=3,  2=3,  =1,5 , 

                               х-1=2,25 , х=3,25

  Перевірка:

  Відповідь:  3,25.

 

Зробимо невеличку перерву з користю, отримавши додаткову інформацію. Виступ доповідача з історичною довідкою.

 

 Поняття степеня виникло в давнину у зв’язку з необхідністю обчислення площі квадрату та об’єму куба (звідси й пішли назви «квадрат» і «куб» ). Збереглися таблиці квадратів і кубів, складені за 1700 років до нашої ери у древньому Вавілоні.

 Сучасні назви степенів запропоновані голландським вченим Симоном  Стевіном (1548-1620). Він перший почав використовувати дробові показники степеня для позначення коренів. У наш час для добування кореня вживають для позначення: знак радикала і дробові показники. Причому позначення за допомогою радикалів є давньою традицією.

 Наближені значення квадратних коренів з цілих чисел уміли обчислювати ще в древньому Вавилоні близько 4 тисяч років тому.

 З степенями і коренями працював відомий іранський математик і астроном ал-Каші ( ХV).

 Назва «радикал» походить від латинських слів radix-корінь та radikalis – корінний.

  Починаючи з ХІІІ століття європейські математики позначали корінь словом, або скорочено r . У 1525 році у книзі чеського математика Христофора Рудольфа з’явилось позначення для квадратного кореня, для кубічного кореня він користувався знаком ▼▼▼.

У 1626 році голландський математик Альберт Жірар ввів позначення , , …, але тоді писали не , а а+в , сучасне позначення кореня вперше з’явилося  в книзі французького вченого Рене Декарта (1596-1650рр.) «Геометрія».

      Степені з від’ємним показником ввів шотландський математик Вільямс Уолес (1768-1843рр.).

      Дробові показники степеня і найпростіші дії над ними описані в працях французького математика Нікола Ореми (1323-1382рр.). Дробові відношення в степенях Орема називав ірраціональними .

      Подальшу розробку алгоритмів і правил виконання операцій над степенями з дробовими показниками здійснив французький математик Ніколя Шюке (1445-1500рр.).

      П’єр Ферма (1601-1665рр.) в середині   ХVІІ ст. запропонував загальний метод розв’язування ірраціональних  рівнянь, зводячи їх до системи цілих алгебраїчних рівнянь.

 

 

3. Експерт. Застосування властивостей функції. Дослідження ОДЗ дає іноді змогу швидко знайти корінь .

Приклад 1.

ОДЗ :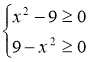            

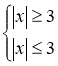
Перевірка :    x₁=     

                       x₂= 3         

Відповідь : - 3 ; 3 .

Приклад 2 :

ОДЗ :

           Нехай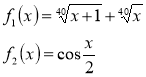 

Знайдемо Є цих функцій

         

, якщо х=0 і cos=1, при х=0 х=0 – розв’язок .

Відповідь: х = 0.

 

4.Експерт: Штучні способи розв’язання .

1.Приклад: у² – 2у

Перейдемо до виду а²+в²=0

у² – 2у

така рівність можлива , якщо у-=0  і  -3=0,

звідси у=    і  х=9.

Перевірка:

Відповідь: ( 9 ; ).

 

Приклад 2.  -=2 , помножимо ліву і праву частину

  рівняння на спряжений вираз :

 ( -)(+)=2(+),

 8=2(+),  звідси

 -=2,

    +=4,   2=6 , х²-х+9=9,         х₁=0   х₂=1.

Перевірка:

Відповідь: 0;1.

 

ІІІ. Розв’язування вправ на закріплення. Декільком учням, за бажанням, пропонуються індивідуальні картки, з збірника Сканаві:

  1.  +=1,               х Є .

  2.    +=7,                 х₁=1, х₂= - .

  3.   - =1,                                   х₁=30, х₂= - 61.

 

 Для колективного розв’язування пропонується приклад:

 

   1 спосіб: стандартне піднесення до степеня.

 

   2 спосіб: зведення до системи раціональних рівнянь.

 

Нехай =а,  =в,    складемо систему:

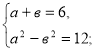
      а=4,  =4,  15-х=16,  х= - 1.

 

Перевірка:

Відповідь: - 1.

 

3 спосіб: множення обох частин рівняння на спряжений вираз.

 

 (+)(-)=6(-),

 12=6(-),   звідси маємо:

  + =6,

-   =2,  звідси  2=8,    15-х=16,   х= - 1.

 

Перевірка:

 Відповідь:  - 1.

 

ІV. Підведення підсумків:

   1.Схема різних способів розв’язання ірраціональних рівнянь.

   2.Домашнє завдання, виконати на вибір 3 завдання ( будь-яким

      способом:

        а) + =3,

        б)  + =2,

        в)  + +   =2,

        г) cosx=,

        д) +=1.

    3.Оцінювання виступаючих, і учнів які працювали біля дошки.