Розробка уроку на тему: "Чотирикутники - зліва, чотирикутники - справа " (8 клас)

Чотирикутники – зліва, чотирикутники – справа.

Урок-семінар з геометрії у 8 класі.

Тема уроку. Чотирикутники.

Мета уроку. Систематизувати й узагальнити знання, вміння і навички учнів про чотирикутники, їх властивості; формувати здатність самостійно аналізувати ситуацію, уміння використовувати набуті знання, розвивати процеси мислення (аналіз, синтез, аналогію, узагальнення); виховувати розуміння учнями важливості геометрії в щоденному житті, мовну культуру учнів та формувати в них різні групи компетенцій:                                                                                                                                                          а) уміння вчитися – індивідуальний досвід участі в роботі на уроці. Бажання організувати свою працю для досягнення успішного результату, творчий підхід до вирішення проблеми;                            б) загальнокультурні (комунікаційні) – опанувати засоби культурного спілкування в ході обговорення питань уроку, розвивати вміння вести групову бесіду;                                                                                    в) соціально-трудові – усвідомлення власного внеску в спільну роботу, готовність робити вибір, уміння відстоювати свою точку зору, прояву ініціативи ;                                                                                    г) інформаційні – уміння використовувати різноманітну інформацію, аналізувати, систематизувати та узагальнювати її, розширення кругозору.

Тип уроку: узагальнення та систематизації знань, умінь і навичок.

Обладнання: таблиця «Чотирикутники», карточки із завданнями, шарнірна модель чотирикутника, креслярські інструменти, набори геометричних фігур, репродукції картин, вишиті рушники, писанки, кольорова крейда.

Попередня робота.                        Приступаючи до вивчення теми «Чотирикутники», я попередила учнів про проведення уроку-семінару і повідомила перелік запитань та завдань, які треба підготувати всім.                                          1. Повторити за підручником і знати означення та властивості вивчених чотирикутників.                            2.Підготувати з клаптиків матерії (паперу) моделі ромба, паралелограма, квадрата і прямокутника.                                                                                                                                                                                      3. Ознайомитися із запропонованою літературою  і написати звіт про чотирикутники:                            - історична довідка;                                                                                                                                                          - показати практичне застосування;                                                                                                                              - значення «чотирикутних» символів у вишивці та писанкарстві;                                                                      - чотирикутники і живопис.

Підручник. Бурда М. І. Геометрія: підруч. для 8 кл. загальноосвіт. навч. закл./ М. І. Бурда, Н. А. Тарасенкова. – К.: УОВЦ «Оріон», 2016.

Девіз уроку: «Ти можеш, він може, я можу !» 

На дошці прикріплені аркуші з написом  «Цей урок навчить мене»:                  ■ дізнатися про застосування чотирикутників у різних сферах життя;                                                        ■ використовувати набуті знання;                                                                                                                              ■ відтворювати, систематизувати та узагальнювати знання про чотирикутники;                                          ■ робити логічні висновки;                                                                                                                                            ■ розв’язувати задачі: геометричні, практичні, пошукові;                                                                                    ■ обмінюватися думками;                                                                                                                                            ■ працювати в парах та групах.                                                                                                                              ■ аналізувати, порівнювати, доводити, висловлювати оцінні судження.

    Хід уроку

І. Організаційно – психологічна частина.       Сьогодні на уроці ми працюватимемо разом і я розраховую на вашу старанну працю на уроці та змістовні відповіді. Кожному з вас хочу побажати, щоб на цьому уроці ви були:                                                        «У» - усміхненими,                                                                                                                                                          «С»- спокійними,                                                                                                                                                          «П» - прогресивними,                                                                                                                                                          «І» - ініціативними,                                                                                                                                                          «Х» - хоробрими.                                                                                                                                            Генрі Форд говорив: «Збиратися разом – це початок,                                                                                                                                            Триматися разом – це прогрес,                                                                                                                              Працювати разом – це успіх».                                                                                                  Іншими словами, я бажаю вам УСПІХУ!

ІІ. Підготовка до свідомої навчальної діяльності: повідомлення теми уроку, визначення мети та мотивація навчання.

Досягти успіху можна тільки тоді, коли є певна мета.  Тому ознайомимося з темою уроку та сформулюємо мету нашого уроку. (Діти висловлюють свої думки).                                                                                    Ми завершили вивчення теми «Чотирикутники». Сьогодні ми маємо узагальнити , систематизувати вивчене, вчитися використовувати здобуті знання та вміння в незвичайних і несподіваних ситуаціях, перевірити теоретичний матеріал і застосувати його до практичних вправ.              Різні властивості чотирикутників досліджували не тільки любителі геометрії, а й найвідоміші вчені всіх епох: Евклід. Ньютон, Ейлер, Гаусс, Лангранж та інші. Виявлені та досліджені ними властивості чотирикутників – справжні перлини людського мислення. Багато з них доступні для розуміння вам, учням, ми їх вже вивчили. Геометрія чотирикутника дає чудовий матеріал для досліджень, у них кожен може знайти цікаві і доступні теми для самостійних пошуків.                                          На нашому уроці присутня експертна група, до складу якої входять дизайнер, історик, художник, біолог, мистецтвознавець, етнограф, конструктор, архітектор.                                                                      Члени цієї групи більш досконало вивчили чотирикутники, встановили нові факти, написали звіти про своє дослідження. І сьогодні нам їх мають повідомити. Але це трохи пізніше.                            А зараз прошу підготувати зошити для роботи. Нагадую, що ділові папери (а для учня зошит є таким) треба вести старанно, охайно та уважно.                                                                                                  Записуємо дату та тему уроку.

ІІІ. Відтворення та корекція опорних знань.

 Знання, що будуть потрібні протягом уроку для виконання різних завдань і задач, повторимо.                                                                                                                                                                                      1. Колективна пошукова робота.                                                                                                                              Розглянути таблицю і виконати завдання (рис. 1).                                                                                                  а) Назвати зображені фігури.                                                                                                                                            б) Записати умови, які використовуються для означення зображених чотирикутників.                            Відповідь:                                                                                                                                                                        1) АВ∥СД, ВС ∥АД.                                                                                                                                                          2) АВ∥СД, ВС∥АД, А=⦟В=90°.                                                                                                                              3)АВ∥СД, АВ∥ВС, ⦟А=⦟В=90°, АВ=ВС=СД=АД.                                                                                                  4) АВ∥СД, АД∥СД, АВ=ВСД=ДА.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      Рис.1.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                            2. Чи є дана фігура чотирикутником (так чи ні)?

                                                                                                                                                                                                                                                                                                                                                                                                                     1                                    2                                      3                                                                      4                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                    3. Гра «Художник - геометр». (Колективна робота).                                                                                                  Всі ви, мабуть, із задоволенням відвідували уроки образотворчого мистецтва. А зараз ви побуваєте у ролі художників-геометрів. На дошці зображена таблиця, яка потребує ваших знань геометрії і творчих здібностей. Треба впізнати про яку геометричну фігуру йдеться, з’єднати стрілками вислови із назвою фігури та її зображенням. Кожен учень робить одне з’єднання.              

                           4. Усе, що знаю про неї – розкажу. (Інтерактивна вправа «Мікрофон»).                                                        Вам потрібно розповісти про геометричну фігуру трапецію: зображення, означення, властивості, цікаві факти. (Під час розповіді можна використовувати таблицю «Чотирикутники»).                            Зразок відповіді про трапецію.                                                                                                                              1.Означення трапеції.                                                                                                                                                          2. Трапеції бувають: рівнобічні, різнобічні, прямокутні.                                                                                    3. У прямокутної трапеції два кути прямі.                                                                                                                4. У рівнобічної трапеції бічні сторони рівні. Кути при основі рівні, діагоналі рівні.                                          5. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.                                                                      6. Слово «трапеція» - походить від грецького слова «трапедзіон». Воно колись означало столик. Термін трапеція спочатку застосовувався в розумінні будь-якого чотирикутника і лише у ХVІІІ ст.. набув сучасного змісту. До речі, цей термін і слово «трапеза», яке є застарілим українським словом, мають той самий корінь та спільне походження. Це пов’язано з тим, що в давні часи столи мали профіль рівнобічної трапеції. Інколи такі столи можна побачити й зараз.                            

5. Індивідуальна перевірка знань.         Учні заповнюють узагальнюючу таблицю з теми «Чотирикутники».

Узагальнення і систематизація знань.      Відмітити знаком «+» властивості, характерні для даних фігур.             

6. Підкресліть зайве слово:                        а) у ромба, квадрата, прямокутника, рівнобічної трапеції діагоналі рівні;                                                        б) у ромба, прямокутника, квадрата сторони рівні;                                                                                    в) у ромба,паралелограма, квадрата діагоналі перетинаються під прямим кутом.             

7. Які із зображених чотирикутників на рис. трапеції? Які з них прямокутні, а  які рівнобічні трапеції?                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   ІV. Використання  набутих знань і навичок під час розв’язування задач.

1. Розв’язування геометричних задач.       Розв’язування задач з підручника, розміщених на стор. 66.                                                                      № 1-4.
2.      Розв’язування практичних задач.         Французький математик Рене Декарт (1596-1650)говорив: «… у математичних науках є дуже вдалі винаходи. Здатні принести велику користь, задовольняючи любов до знань, полегшуючи всі ремесла і скорочуючи працю людини».                                                                                                  Отже, ви зараз розв’яжете практичні задачі, використавши знання по темі «Чотирикутники».                                                                                                                                                                        а ) Навести приклади використання властивостей чотирикутників на практиці.                                          Очікувані відповіді.                                                                                                                                                          ■ Є предмети і деталі, що містять моделі паралелограмів   (шарнірна модель, дротяна сітка, віконна рама,…), трапеції (мостова ферма, пасова передача, кронштейн, стіл,…).                                          ■ Вивчені властивості та ознаки паралелограма мають численні практичні застосування: у конструкції відкидних драбин. Які застосовуються у пасажирських залізничних вагонах; у столярній та будівельній справі (двері, перила на східцях), дія креслярських приладів (креслярські лінійки. кульмани).                                                                                                                                                                                      ■ «Нежорсткість» чотирикутника. Уявіть модель чотирикутника, зроблену із шарнірно сполучених планок. Ми можемо змінювати величини кутів чотирикутника, а довжини сторін залишаються без змін. А це свідчить, що існує безліч таких чотирикутників із заданими довжинами сторін. З фізичної точки зору це означає нежорсткість шарнірного чотирикутника, тобто можливість різних його  трансформацій без зміни довжини сторін.                                                                                     Цей факт широко використовується у техніці для створення шарнірних механізмів. Слід нагадати, що на відміну від чотирикутника, трикутник є жорсткою фігурою.                                                                      ■ Найпоширенішим видом чотирикутника є прямокутник. Ще давні єгиптяни надавали своїм земельним ділянкам прямокутної форми. Прямокутну форму мають плани і більшість складових архітектурних споруд я давнини, так і сучасності, зокрема наша школа. Прямокутник є визначальним структурним елементом одного з найпоширеніших у застосуваннях геометричного тіла – прямокутного паралелепіпеда. Прямокутні форми – найпоширеніші при упорядкуванні природних ландшафтів.                                                                                                                                                          ■ Прямокутник називається « золотим», якщо відношення його сторін 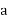і в рівне 1,62, тобто  =1,62. Ще стародавні греки вважали, що прямокутники, довжини сторін яких утворюють відношення золотого перерізу, найприємніші для ока. Тому такі форми є найбільш поширеними – від книжкових обкладинок до письмових столів, від вікон до фасадів будинків, від кредиток до гральних карт тощо.                                                                                                                                                                        Проведемо експеримент. Із даних прямокутників виберіть той, що вам найбільше сподобався. (Серед запропонованих прямокутників один має відношення сторін рівне золотому перерізу 1,62. Учні вибирають і вчитель повідомляє їм про результат вибору).                                                        ■ Перпендикулярність діагоналей ромба застосовується у  чотириланкових шарнірних механізмах для реалізації прямолінійного поступального руху. Одним із найпоширеніших прикладів такого застосування є домкрат. Іншим прикладом є механізм так званого відцентрового регулятора, який відіграв виняткову роль в епоху парових машин. Його сконструював видатний англійський винахідник (у тому числі парової машини) Джеймс  Уатт  (1736-1819) для регулювання подачі пари у паровій машині. Фактично та сама геометрична ідея, але уже з поєднанням декількох ромбів, втілюється в оригінальній конструкції утримувачів, наприклад, для машин та дзеркал, якщо ці предмети час від часу потрібно зміщувати у певному напрямку.                                                        б) Пропоную практичні задачі для усного розв’язання.                                                                                    Із фанери випиляли квадрат. Як перевірити, що відрізаний чотирикутник є справді квадратом?                                                                                                                                                                                      Вказівка. Повернути чотирикутник на 90° і встановити в розріз, що утворився у фанері.                            в) Майстер-паркетник хоче бути упевненим в тому, що чотирикутники, які він випиляв, - це квадрати.                                                                                                                                                                                      Чи достатньо для цього:                                                                                                                                            - рівності чотирьох сторін; (ні, чотирикутник може бути ромбом);                                                                      - рівності двох діагоналей; (ні, чотирикутник може бути прямокутником);                                                        - рівності чотирьох сторін та рівності двох діагоналей (так).                                                                                    3. Розв’язування пошукових задач.                                                                                                                              ( Робота у парах).                                                                                                                                                          а) Як із прямокутного куска тканини вирізати квадратну хустинку, користуючись лише ножицями?

                                                                                                                                                                                                                                                                                                                                                                                                                                                                 б) Складіть трапецію із квадрата і прямокутного  трикутника.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

 (Робота у групах).

в) Відновіть паралелограм, якщо на рисунку збереглися сторона АВ і точка перетину діагоналей.(Хід  побудови учні обговорюють у групах, а потім представник групи, яка найшвидше впоралася із завданням, демонструє правильну відповідь на дошці).                                                                      г) Ділова гра «Настилання паркетної підлоги».                                                                                                  Завдання. Виконати настилання паркетної підлоги в залі, який має форму прямокутника. Паркетні плитки мають форму прямокутних трапецій, паралелограмів, рівнобедрених трапецій. Після настилання підлоги не повинно лишитися зайвих плиток і проміжків між ними. (Для економії часу на уроці це завдання можна дати як домашнє випереджувальне завдання , а на уроці обговорити результат).                                                                                                                                                          Розміри плиток:                                                                                                                                                                         паралелограм: висота-20мм, сторона, на яку опущена висота,-35мм;                                                        прямокутна трапеція: висота-20мм, більша основа-35мм;                                                                                    рівнобедрена трапеція: висота-20мм, меша основа-20мм, більша основа-65мм.              4. Геометричний тренінг.                                                                                                                                            а) Трапеція – священна фігура піфагорійців. У кожному домі обов’язково було що-небудь «трапеційне», яке захищало членів родини від усіх бід і негараздів. У нас є «священна» картина тих часів. Покажіть, де на ній зображено трапеції і порахуйте скільки їх.                            Відповідь: 12 трапецій.                                                                                                                                             б) Скільки чотирикутників на рисунку? (8 чотирикутників).                                                                                                               

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             V. Чотирикутники – зліва, чотирикутники – справа.

1. «Квадратні» дива природи.                      Біолог. Невідомий досі вид дерев із стовбурами, що мають не круглий. А квадратний переріз, доглядають ботаніки в провінції Чжецзян у Китаї. Тут на площі близько 50 квадратних метрів, росте 120 таких дерев заввишки 3-5 метрів. Дерево з чотирикутним стовбуром – це ж готова шпала, що не потребує обробки!               В Японії «квадратні кавуни» вивів селекціонер Томоюкі Оно, не використовуючи при цьому ніяких хімікатів. Такого результату він досяг, вирощуючи кавуни у спеціальних горщиках. Вони зберегли смак, але набули нових переваг: зручно ділити на дольки, легко відділяти шкірку, викладати при транспортуванні. Вирощують «квадратні » помідори в Ізраїлі.                                                        На замовлення авіакомпанії генетики США вивели сорт кукурудзи з «квадратними» зернами. Під час «повітряних» обідів у польоті вона не скочується з тарілок.                                                        2.Чотирикутники і мистецтво.                                                                                                                              Художник. В живописі велику роль відіграє формат картини і вибирають його художники дуже ретельно. Найчастіше вони надають перевагу прямокутному (вертикальному або горизонтальному) формату, колу (тондо). У прямокутниках компонують зображення в тій чи іншій геометричній формі, іноді розгортають дію по діагоналі. Розглянемо репродукції деяких творів живопису. (Приклади прямокутного (горизонтального та вертикального) формату). Формат картини пов'язаний із стилем епохи, із особливостями техніки живопису, композиції, інтер’єру для  якого призначена картина.                                                                                                                                                          Мистецтвознавець. А зараз ми відвідаємо музей однієї картини – всесвітньо відомої і багатьма оспіваної, майже легендарної… А в тім, кожен з вас може при бажанні виконати її копію. Що ж це за картина?                                                                                                                                                                        (Відкривається дошка і з’являється чорний квадрат на білому).                                                                      Це картина «Чорний квадрат», яку створив художник Казимир Малевич (1878-1935) і цією роботою заснував школу авангардного мистецтва.                                                                                                                Дивна річ – найпростіші зображення можуть створити настрій. Придивіться. Комусь квадрат бачиться страшною діркою, а комусь – бездонною криницею, в яку хочеться впасти – так вона тремтить і вабить. Квадрат, як показує Малевич, володіє всіма якостями образу – як квітка чи акорд.                                                                                                                                                                                                    Картина «чорний квадрат» Малевича, дитинство та юнацькі роки якого пройшли на Україні, стала початком створеного ним напрямку – супрематизму.                                                                                                  Суперматизм – вид абстрактного мистецтва ХХ ст..: комбінування зафарбованих найпростіших геометричних фігур (квадрата, полос, трикутника тощо).  Суперматизм значно вплинув на розвиток декоративно-оздоблювального мистецтва та стиль меблів. Посуду, одягу, зачісок і навіть на оформлення друкованих видань та виготовлення різнокольорової тари, що має чотирикутні форми.                                                                                                                                                                         «Чорних квадратів» Малевича (як і виконав сам автор) офіційно відомо щонайменше п’ять.              3. Квітнуть наші вишиванки, ніби райдуги співанки.                                                                                                  Дизайнер. Вишивка – один з давніх і найбільш розповсюджених видів мистецтва. Вона виникла давно і передавалася від покоління до покоління.                                                                                                   Ще у глибоку давнину люди навчилися створювати нескладні малюнки з умовних знаків-символів, де кожна лінія чи фігура мали певне значення. Так , сонце зображали у вигляді ромба або квадрата.                                                                                                                                                                                      Ромб з подовженими сторонами означає будівлю, а квадрат розділений на чотири частини з крапкою у кожній символізував поле чи садибу.                                                                                                                А зараз поглянемо на розмаїття барв, що оселилися сьогодні в нашому класі. На нашій виставці представлені рушники, що збереглися у ваших родинах. У вишивці майстрині відтворили свої заповітні мрії про майбутнє.                                                                                                                                            Розгляньте у вибраному рушнику геометричні узори і поясніть їх символічне значення.                            4. Знаки писанок логічні, кольорові символічні.                                                                                                  Етнограф. Писанка – по-мистецькому розписані великодні яйця. Погляньте,які писанки різні за орнаментом. Ці орнаменти – це не просто малюнки, а таємничі знаки.                                                                                     Знаки долю прихиляють,                                                                                                                                            Лихо відвертають.                                                                                                                              Досить популярними є геометричні символи, яйце ділиться простими лініями на трикутники, квадрати, ромби, пояски.   «Ромб» є символ родючості. «Квадрат», поділений на частини з крапками був символом засіяного лану.                                                                                                                5. Про походження цифр.                                                                                                                                            Історик. Чимало людей намагалися пояснити форму арабських цифр. Цікавило це питання й Олександра Сергійовича Пушкіна. Він знайшов своєрідну відповідь на нього: сучасні цифри складено з прямокутника з двома діагоналями.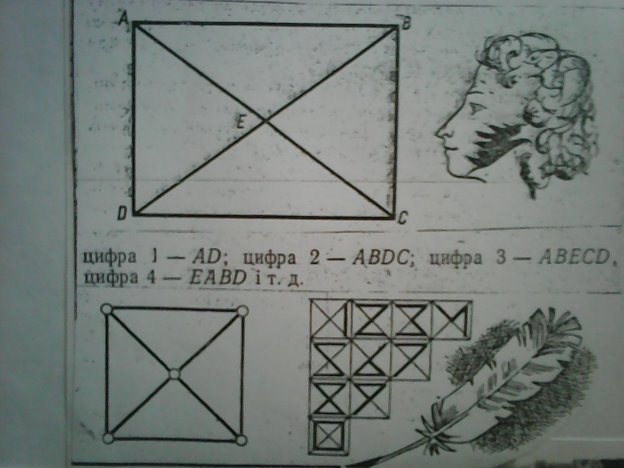                                                                                                 

VІ. Підведення підсумків уроку.                     1. Пояснити діаграму на стор. 33 підручника.                                                                                                  2. Інтерактивна вправа «Мікрофон».                                                                                                                              Запитання.                                                                                                                                                                        а) Чи потрібно вивчати властивості чотирикутників?                                                                                                  б) Чи потрібно цю тему включати до шкільної програми?                                                                                    3. Осмислення результатів уроку (рефлексія).                                                                                                   - Що ми робили на уроці?                                                                                                                                            - Чому ми цим займалися?                                                                                                                                            - Чи вдалося нам досягти мети уроку?                                                                                                                - Що сподобалос я і що не сподобалося на уроці?                                                                                                  - З ким приємно було працювати?                                                                                                                              - Які ваші пропозиції?                                                                                                                                                          4. Виставлення оцінок.                                                                                                                                            Учитель оцінює роботу учнів на уроці.                                                                                                                На високому рівні виявили свої творчі здібності, уміють розв’язувати задачі високого рівня такі учні…                                                                                                                                                                                      На достатньому рівні вміють узагальнювати і систематизувати навчальну інформацію, формулювати і застосовувати основні властивості чотирикутників…                                                                                    Учні, які знають властивості чотирикутників, але не завжди їх вміють застосувати, заслуговують на найвищу оцінку середнього рівня. Це такі учні…

VІІ. Повідомлення домашнього завдання.                   Повторити $ 1-5, розв’язати задачу № 254, 256.                                                                                                  Пошукове завдання. Знайти відношення сторін предметів прямокутної форми та порівняти з числом 1,62. Зробити висновки.                                                                                                                                            Вчитель.  Мудрець сказав: «Дві людини, які обмінялися золотими монетами , не стали багатшими. Але якщо вони обмінялися думками, то кожний з них став вдвоє розумнішим. Адже обидва стали тепер  розумнішими».                                                                                                                                            Ця притча проста,  але зміст її глибокий. Обмінюючись думками, ідеями, досвідом, знаннями, люди нічого не втрачають. А багато чого набувають – нових знань.                                                        Ось і ви сьогодні дізналися багато нового про чотирикутники. Я сподіваюсь, що кожен із вас щоденно наполегливо буде підніматися по крутих схилах науки геометрії впевнено крокуючи до нових знань.                                                                                                                                                                                      Бажаю вам успіхів у освоєнні «геометричного океану знань».                                                                      Урок закінчено, до зустрічі на наступному уроці!

Використана література.                      1. Тадеєв В. О. Геометрія. Вимірювання многокутників: Базовй курс. Підр. для 8 кл. загальноосв. Навч. закл. – Тернопіль: Навчальна книга – Богдан, 2008.                                                                      2. Гін В. І. Прийоми педагогічної техніки. – Х.: Веста: Вид. «Ранок», 2007.                                                        3. Підручна Марія. Позакласна робота з математики. 8-9 класи. /М. Підручна, Г. Янченко. – Тернопіль: Підручники і посібники, 2000.                                                                                                                              4. Сухарева Л. С. Дидактичні ігри на уроках математики. 7-9 класи. – Х.: Основа, 2006.                            5. Далингер В. А. Методика реализации внутр. Предметних связей при обучении математики. Кн. Для уч. – М.: Просвещение, 1991

.  

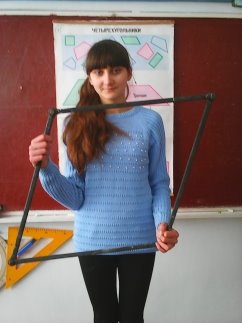
Демонстрація нежорсткості чотирикутника за допомогою шарнірної моделі.