Урок : "Розв’язування прямокутних трикутників. Прикладні задачі"

Тема уроку: Прикладні задачі. Розв’язування прямокутних трикутників

Мета уроку: Показати застосування розв’язування трикутників до розв’язування прикладних задач (визначення відстані до недоступної точки, висоти предмету тощо). Здійснювати міжкурсові та міжпредметні зв’язки. Розвивати логічне мислення, вміння застосовувати теоретичний матеріал до розв’язування вправ. Виховувати самостійність, інтерес до предмету. Розширювати кругозір учнів.

Обладнання: таблиці Брадіса, ілюстрації, довідник „Планіметрія”, портрети Архімеда, Фалеса, Г. Галілея, енциклопедії, ілюстрації.

Тип уроку: урок набуття вмінь і навиків.

Форма проведення: урок- подорож.

                                            Хід уроку

І. Актуалізація опорних знань учнів.

Повторити основні види розв’язування трикутників по довіднику „ Планіметрія ” .

ІІ. Мотивація пізнавальної діяльності учнів.

Розв’язування трикутників знаходить широке застосування при розв’язуванні великого класу задач практичного характеру. Розв’язування трикутників необхідне і геодезисту , і картографу, і навіть футболісту.

ІІІ. Повідомлення теми та мети уроку.

Девіз уроку: „ Приклади іноді корисніші від правил ” (І.Ньютон)

ІV. Розв’язування вправ.

До нашого часу дійшли легенди, про те що Архімед вмів швидко і вправно та безпомилково знаходити відстань до недоступної точки. (портрет вченого).

Задача. Щоб виміряти відстань від точки А на березі моря до точки В в морі діють наступним чином. Відклали на березі моря відстань АС=1200 м і визначили кути

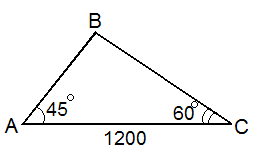
Розв’язання.

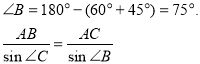
м.

Задача. Місто Александрія - столиця держави Птолемеїв. Тут на острові Фарос, було побудовано маяк. Відкрите вогнище з дров, що запалювали вночі на найвищій терасі маяка, було видно на відстані 50-60 кілометрів. Простояв маяк 1500 років. Найвищу круглу терасу маяка, відкриту з усіх боків, де вночі запалювали вогнище оточувала пірамідальна вежа, увінчана бронзовою статуєю покровителя морів Посейдона, заввишки 8 метрів.

 Знайти висоту Алексанрійського маяка, якщо з однієї точки маяк видно під кутом , а коли віддалитися від маяка ще на 500 метрів, то його видно під кутом .

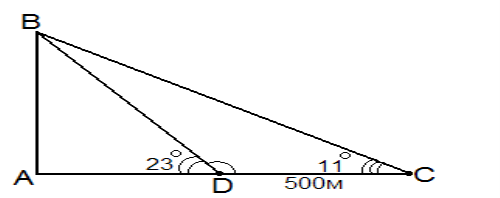
                                    Розв’язання

1.

2.

3.м.

Задача. (ілюстрація Пізанської вежі та портрет Г. Галілея)

Пізанська вежа. На цій вежі італійський фізик, механік, астроном, математик Галілео Галілей проводив досліди і визначив прискорення вільного падіння. А ще вона відома тим, що з кожним роком все більше нахиляється до землі.

Кожен предмет має центр мас і нахилившись він упаде, коли перпендикуляр, проведений з центра мас до площини основи предмета, вийде за межі основи. Давайте з’ясуємо, при якому куті нахилу вежі вона мала б упасти, якщо діаметр основи 18,8 м, а відстань від центра мас вежі до центра її основи 16,4 м.

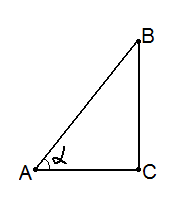
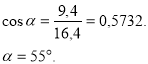
(При цьому слід враховувати фундамент вежі, закопаний в землю. Ось чому, щоб зберегти унікальну пам’ятку історії і науки вчені проводять роботи по зміцненню фундаменту). Цікаво, що висота Пізанської вежі 67,15 м, тоді як висота дзвіниці Києво-Печерської лаври 96,52 м. Вона теж відхилена від вертикалі (ілюстрація).

Задача. В Африці серед Лівійської пустелі, на скелястому плоскогір’ї, що відокремлює долину Нілу від мертвої пустелі, височать піраміди, вишикувавшись в ряд майже на 100 км від Каїра до Фаюма. До наших часів збереглось близько 70 пірамід. Найвідоміші з них – Хеопса і Хефрена. Найбільша з них – велика піраміда Хеопса, збудована в 28 столітті до нашої ери. Висота її 147 м, площа основи 54000м. Згідно з легендами, піраміда служила фараонам тією драбиною, якою вони сходили в небо.

(Ілюстрація піраміди)

Піраміди - одне із семи чудес світу. Кожний , хто приїздить подивитися на них, мріє піднятися на вершину.(Як потрібно підніматися, гранню чи ребром?) За скільки часу турист підніметься на вершину піраміди Хеопса, якщо він рухатиметься зі швидкістю 0,5км/год.

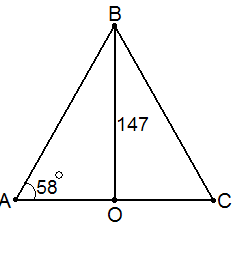
1)м

2)0,5 км/год=м/хв.

Давньогрецький математик Фалес вмів визначати висоту піраміди за тінню. Чим в свій час здивував єгипетського фараона Амазіса.

На Полтавщині ми маємо прототипи єгипетських пірамід. Вони менших розмірів, але науковці говорять про цілющі їх властивості. Це піраміда - усипальниця Закревських в селі Березова Рудка Пирятинського району( як поховання зруйнована), піраміда в селі Комендантівка Кобеляцького район та сучасна піраміда в селі Кіндрівка Кременчуцького району.

ІV. Підсумок уроку. Цінування та оцінювання відповідей учнів

Метод «Чотири ЩО?»

1. Що ви дізналися, навчилися на уроці?
2. Що сподобалося найбільше?
3. Що було найскладнішим?
4. Що треба ще вивчити?

V. Домашнє завдання.1.Диференційована домашня самостійна робота

Творче.Скласти прикладну задачу