Розробка уроку на тему "Пряма і правильна призми. Площі бічної і повної поверхні призми"

ПЛАН УРОКУ

Тема уроку. Пряма і правильна призми. Площі бічної і повної поверхні призми.

Мета уроку:   формування понять пряма, похила і правильна призми; вивчення теореми про бічну поверхню прямої призми.

Формування компетентностей:

предметна (математична) компетентність: сформувати поняття многогран­ника, вершин, ребер, граней многогранника, призми та її елементів (основ, бічних граней, бічних ребер, висоти, діагоналі), прямої та похи­лої призми, правильної призми; домогтися засвоєння властивостей призми та пря­мої призми; сформувати вміння розв'язувати задачі, що передбачають застосуван­ня цих понять;

ключові компетентності:

спілкування державною мовою — уміння розуміти, пояснювати й перетворюва­ти тексти математичних задач (усно й письмово), грамотно висловлюватися рід­ною мовою;

інформаційно-цифрова компетентність — уміння доводити істинність твер­джень;                           

уміння вчитися впродовж життя — уміння визначати мету навчальної діяльнос­ті, відбирати й застосовувати потрібні знання та способи діяльності для досяг­нення цієї мети;

соціальна та громадянська компетентність — уміння аргументувати та захи­щати свою позицію;

Тип уроку:удосконалення  знань і вмінь.

Основні терміни і поняття: багатогранник, призма, пряма і правильна призми.

Наочність: макети багатогранників, моделі прямої, похилої та правильної призм,  картки-завдання, електрона презентація, опорний конспект, схема «Види призм», підручник Мерзляк А . Математика 11 клас, рівень стандарту.

Технічні засоби навчання: мультимедійна система, комп'ютер.

 Хід уроку

І. Організаційний етап

ІІ. Актуалізація опорних знань та вмінь

     Фронтальне опитування

1. Многогранник та його елементи (вершини,ребра, грани)

2. Опуклі многокутники. Приклади опуклих многокутників.

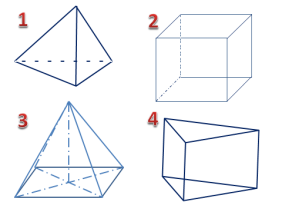3. Яку найменшу кількість граней має многогранник?

4. З-поміж многогранників (зображених на дошці) вкажіть номер того, у якого:

А)чотири вершини;

Б)шість граней;

В)один чотиригранний кут;

Г)дев'ять ребер.

IIІ. Сприйняття та усвідомлення нового матеріалу

1. Призми та її елементи(основи, бічні грані, бічні ребра, висота, діагональ)

 Термін "призма" грецького походження і буквально означає "відпиляне" тіло.

 Многогранник, у якого дві грані – рівні n - кутники, а решта n граней – паралелограми, називається n-кутною призмою.

 Призма - це багатогранник, який складається з двох плоских багатокутників, які лежать у різних площинах та суміщаються паралельним  перенесенням і всіх відрізків, що сполучають відповідні точки цих багатокутників.

 Призма називається трикутною, якщо її основа трикутник; чотирикутною, якщо її основа чотирикутник і т.д. , n – кутною, якщо в основі n – кутник.

 Кожна призма має бічну і повну поверхні (розглядаємо на моделі призми).

 Бічна поверхня складається з паралелограмів (прямокутників), дві сторони яких є відповідними сторонами основ, а дві інші - сусідніми бічними ребрами призми.

 Повна поверхня, або просто поверхня призми складається з двох основ і бічної поверхні.

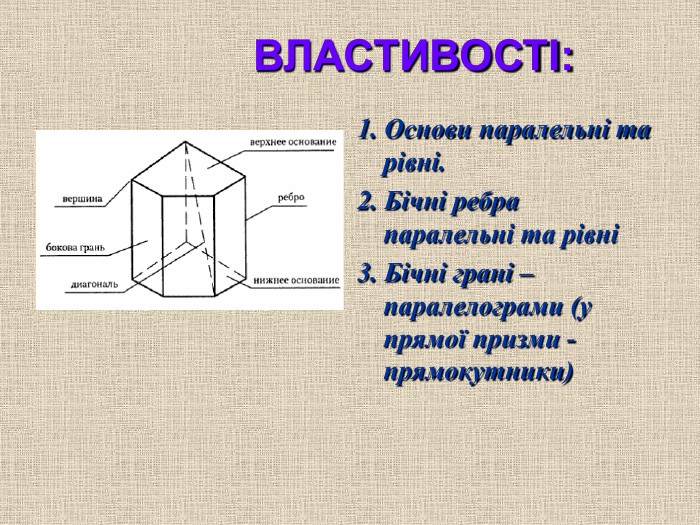
 У всіх елементів призми є свої назви.

Основні терміни й поняття

Висота призми — це перпендикуляр, проведений із будь-якої точки однієї основи на площину іншої основи.

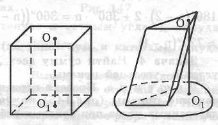
     Ребра призми – це сторони бічних граней і основ. Бічними ребрами називаються ребра, які не належать основами.

Вершини призми – це кінці ребер.

Діагональ призми — відрізок, який сполучає дві вершини, що не на­лежать одній грані.

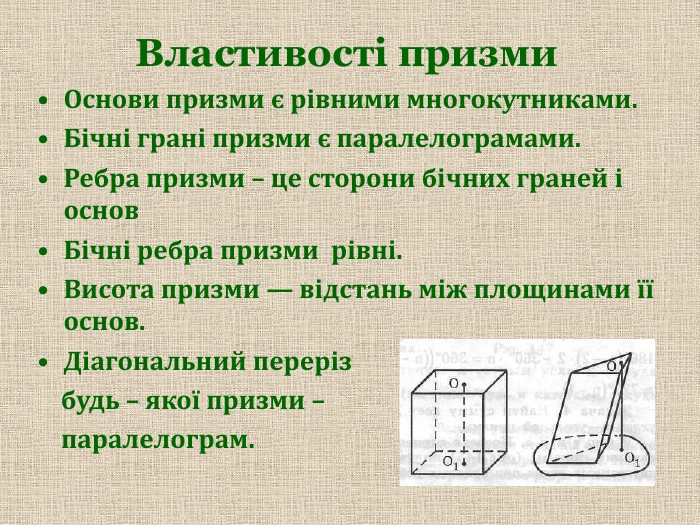
Діагональний переріз призми — переріз призми площиною, яка прохо­дить через бічне ребро й діагональ основи. Діагональний переріз будь – якої призми – паралелограм.

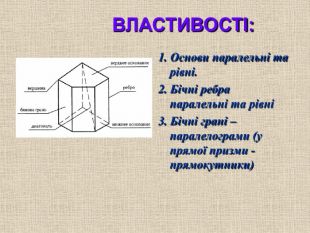
Властивості:

1. Основи призми паралельні і рівні;

2. Бічні ребра паралельні і рівні;

3. Бічні грані - паралелограми

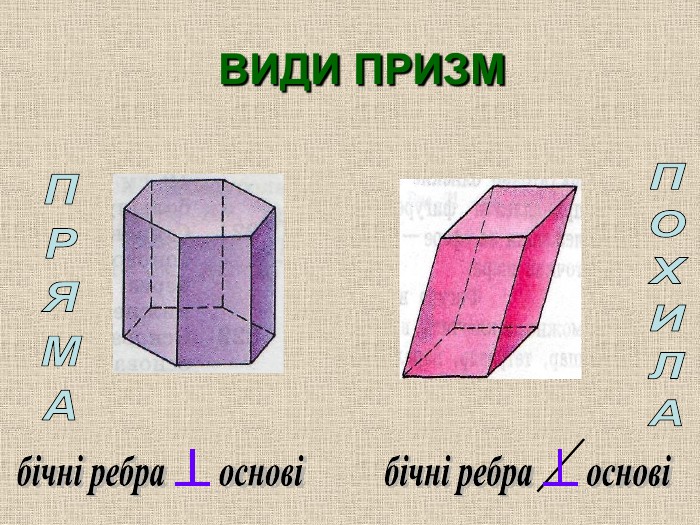
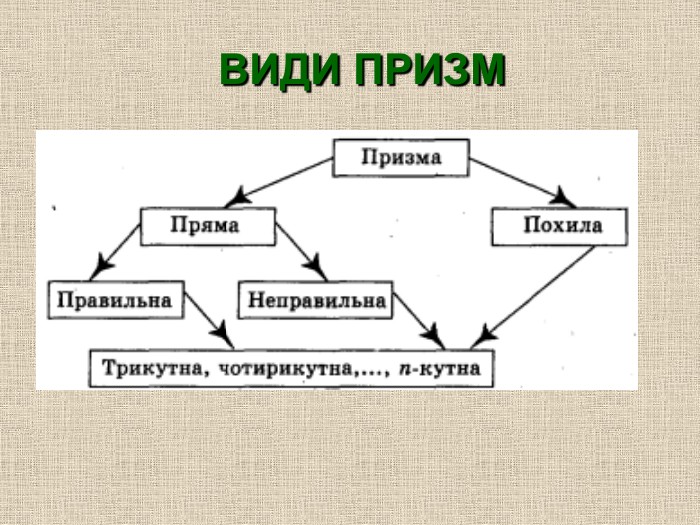
2. Види призм. Пряма. Похилі.

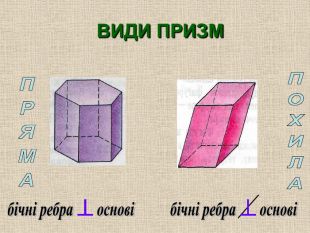
 За видом призми можна поділити на слідуючи групи:  прямі і похилі

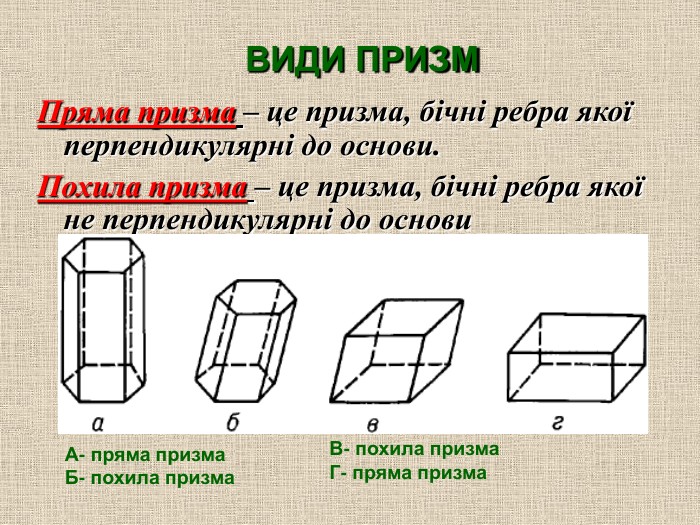
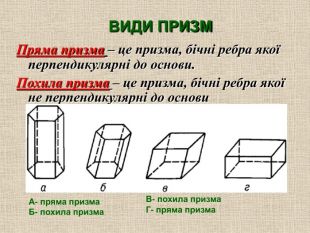
Пряма призма – призма у якої бічні ребра перпендикулярні основам.

  Призма, яка не є прямою, називається похилою.

 Бічні грані похилої призми – паралелограми.

 Демонструються моделі прямих і похилих призм.

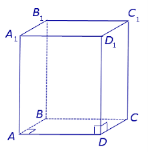
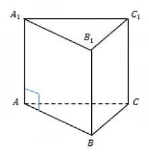
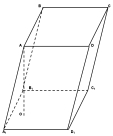
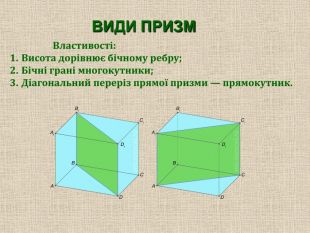
Пряма чотирикутна призма      Пряма трикутна  призма          Похила призма

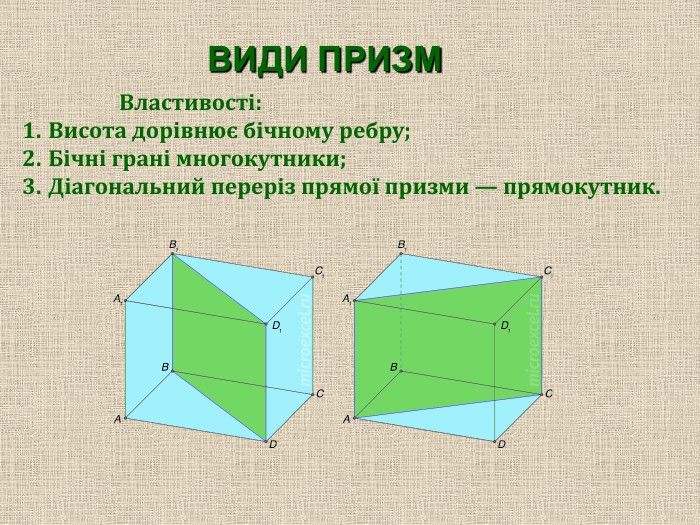
 Бічні ребра прямої призми є її висотами. Бічні грані прямої приз­ми — прямокутники. Бічні грані похилої призми — паралелограми.                           

Діагональний переріз прямої призми — прямокутник.

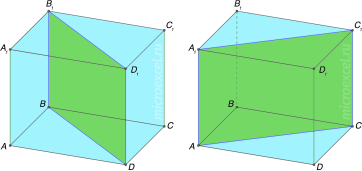
 Властивості:

1. Висота дорівнює бічному ребру;

2. Бічні грані многокутники – Якщо пряма АА₁ перпендикулярна площині основі, то вона перпендикулярна будь – якій прямій, яка лежить в цій основі. АА₁АВ; АА₁AD, тоді звичайно це будуть прямокутники.

 Цю властивість ми будемо застосовувати при розв’язуванні задач.

3. Правильна призма

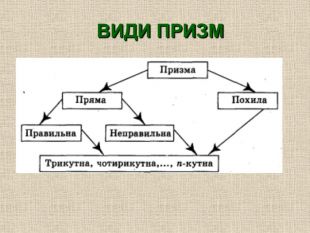
Прямі призми в свою чергу поділяють на правильні і неправильні.

Правильна призма – в основі лежить правильний многокутник.

Всі бічні грані – рівні прямокутники.

Демонструються моделі правильних призм.

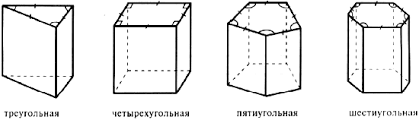
 Тобто, якщо вона правильна, то вона по – перше, пряма, по друге, в основі лежить правильний многокутник: квадрат або рівносторонній трикутник. Всі бічні грані правильні многокутники.

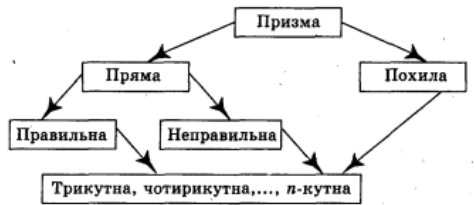
Площа бічної поверхні

Бічна поверхня – складається з бічних граней, тобто, щоб знайти площу бічної по верхні  треба знайти площу кожного з цих прямокутників, а потім додати ці плошці. Але на практиці рахувати площу кожного з прямокутників не потрібно. Чому?

Якщо обраховувати полощу прямокутника  АА₁DD₁, то необхідно сторону AD помножити на висоту  АА₁. Площа прямокутника DD₁СС₁ дорівнює DС ∙D₁С₁; площа ВВ₁СС₁ дорівнює ВС∙ СС₁; площа АА₁ВВ₁ дорівнює АВ ∙ АА₁. Де АА₁= ВВ₁ = СС₁ = DD₁ – висота H. Можна записати S_б = AD ∙ H + AB ∙H + BC ∙ H + CD ∙ H = H(AD + AB + BC + CD).

 Ми бачимо, що AD + AB + BC + CD – це периметр основи нашого многокутника. Отже не потрібно для знаходження площі бічної поверхні рахувати площу кожної грані окремо. Можна використати формулу 

S_б = Р_осн ∙ H. Повна поверхня складається з бічної поверхні та двох площ основи, які теж рівні. S_п = S_б + 2S_осн.

Запам’ятайте !

S_б = Р_осн ∙ H        S_п = S_б + 2S_осн

H – висота призми

Р_осн – периметр основи

S_б – площа бічної основи

Площею бічної поверхні (бічною поверхнею) призми називаєть­ся сума площ бічних граней. Повна поверхня призми дорівнює сумі бічної поверхні і площ основ: S_пр = S_біч + 2S_осн

Розв’язування задач.

Задача 1

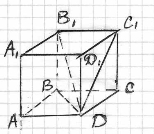
 В основі прямої призми лежить квадрат. Діагональ призми 13 см, висота 5 см. Знайти довжину діагоналі бічної грані. 

Дано:                                                                            

АВСDА₁В₁С₁D₁ – пряма призма

АВСD – квадрат

В₁D – діагональ призми; В₁D = 13см

 АА₁ – висота; АА₁ = 5 см

Знайти: DС₁ – ?

Розв’язання: З ВВ₁D (90^о) за теоремою

Піфагора В₁D² = ВВ+ ВD²

ВD² = В₁D² – ВВ ВD² = 13² – 5² = 169 – 25 = 144; ВD = = 12 (см). Тепер знайдемо сторону основи. В основі лежить квадрат.

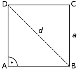
 Треба запам’ятати, що діагональ квадрата d = a - корисний факт. Хто не знає, тоді знаходить за теоремою Піфагора: d² = а² + а²; d² =2а²; d = ; d = a.

З цієї формули знайдемо сторону квадрата: а = ВС =. В нашому випадку

d = ВD = 12 см.  а = ВС = . Звільнюємося від ірраціональності в знаменнику 

ВС = = = = 6(см).

 З СС₁D (90^о) за теоремою Піфагора: С₁D² = DС² + СС; С₁D² = (6)² + 5² =

= 36∙2 + 25 = 72 + 25 = 97. С₁D = (см).

Задача 2

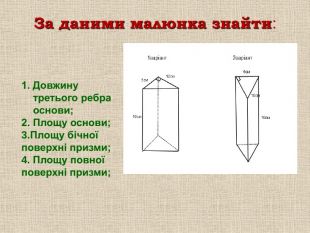
За даними малюнка знайти: 1. Довжину третього ребра основи;

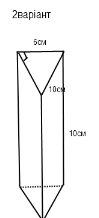
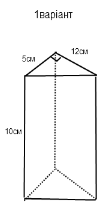2. Площу основи;

3.Площу бічної поверхні призми;

4. Площу повної поверхні призми;

Розв’язання:

В.1. В основі призми лежить прямокутний трикутник. Площа прямокутного трикутник обчислюється за формулою:

1. S_осн = а ∙b =∙5∙12= 30 (cм). 

2. S_біч = Р_осн ∙ H; Р_осн = а + b +с; с –?

 За теоремою Піфагора з знаходимо гіпотенузу с. с² = а²  + b ² = 5² + 12² = 25 + 144 = 169; с = 13 (cм). 

Р_осн = 5 + 12 +13 = 30 см.   S_біч = 30 ∙ 10 = 300 (см²).

3. S_пов. = S_біч  +2 S_осн = 300 + 2∙30 = 360(см²).

В.2. В основі призми лежить прямокутний трикутник. Площа прямокутного трикутник обчислюється за формулою:

1. S_осн = а ∙b; b – ? За теоремою Піфагора з знаходимо катет b.

b ² = с²  -  а ² = 100 – 36 = 64; b  = 8 (cм).  S_осн = ∙6∙8 = 24 (cм). 

2. S_біч = Р_осн ∙ H; Р_осн = а + b +с = 6 + 8 + 10 =24(cм). S_біч = 24 ∙ 10 = 240(см²).

3. S_пов. = 240 +2 ∙24 =240 +48 = 288 (см²).

Задача 3

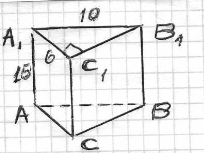
Основа прямокутної призми прямокутний трикутник з катетом 6 см і гіпотенузою 10 см. Висота дорівнює 15 см. Знайдіть площу  поверхні призми.

Дано:

АВ СA₁B₁С₁ – призма

А₁B₁ = 10 см; А₁С₁ = 6см; АА₁ = H = 15 см

Знайти: S_пов. – ?

Розв’язування: S_пов. = S_біч  +2 S_осн

S_біч = Р_осн ∙ H; Р_осн = А₁С₁ + B₁C₁ + A₁B₁

S_осн = А₁С₁ ∙ B₁C₁. 

 За теоремою Піфагора з А₁B₁С₁(С = 90^о)

(B₁C₁)² = (А₁B₁)²  - (А₁С₁)² = 10² - 6² = 100 – 36 = 64; B₁C₁ = = 8(см)

Р_осн = 6 + 8 + 10 = 24(см); S_біч = 24∙15 = 360(см²)

S_осн = 6∙8 = 24(см²); 2S_осн = 2∙24 = 48(см²).

S_пов. =  360  +48 = 408(см²).

IV. Підведення підсумку уроку

Запитання до класу

1) Дайте означення прямої (похилої) призми.

2). Дайте означення правильної призми.

3) Перелічіть властивості прямої призми.

4) Перелічіть властивості правильної призми.

5) Що таке бічна поверхня призми (повна поверхня призми)?

6) Чому дорівнює бічна поверхня прямої призми?

7) Дано пряму шестикутну призму . Укажіть, які із наведе­них тверджень правильні, а які — неправильні:

а) всі бічні грані призми — рівні прямокутники;

б) всі бічні грані — прямокутники;

в) висота призми дорівнює бічному ребру;

г) всі діагональні перерізи рівні.

На цьому і на наступних уроках можна використовувати довідкову схему «Правильні многокутники».

V. Рефлексія

Продовжить фразу:

- Мені було цікаво...

- Ми сьогодні розібралися...

-Я сьогодні зрозумів, що...

- Мені було важко...

- Завтра я хочу на уроці     

VІ. Домашнє завдання: вивчити зміст понять ,розглянутих на уроці:

 Підручник Мерзляк А . Математика 11 клас, рівень стандарту.

           §16, с.99 – 101, вправ 16.7,16.8, 16,10.

 Розв’язки д/з

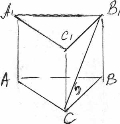
16.7.°  Сторона основи правильної трикутної призми дорівнює 5 см, а  діагональ бічної грані — 13 см. Знайдіть висоту призми.

Дано:

АВСA₁B₁С₁ – призма;

АВС – р/с трикутник;

СB₁ – діагональ; СB₁ = 13 см;

СB – сторона основи; СB = 5 см

Знайти: ВB₁ – ?

Розв’язок: З СВB₁ за теоремою

Піфагора ВB₁ = (СB₁)² – СВ² = 13² – 5² = 169 – 25 = 144; СB₁ = 11 (см)

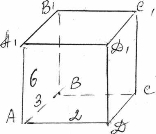
16.8.° Знайдіть площу бічної поверхні прямої призми, висота якої дорівнює 6 см, а основою є паралелограм зі сторонами 2 см і 3 см.

Дано:

АВСDA₁B₁С₁D₁ – призма; АA₁ =  6 см

АD = 2 см; АВ = 3 см

Знайти: S_біч – ?

Розв’язок: Р_осн ∙ H; Р_осн = 2(АВ + АD);

Р_осн = 2(3 + 2) = 10(см); S_біч = 10∙6 = 60(см²)

16.10.° Знайдіть площу повної поверхні правильної чотирикутної

призми, сторона основи якої дорівнює a, а висота дорівнює H.

Дано:

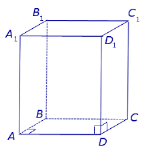АВСDA₁B₁С₁D₁ – призма; АВ = а;

А A₁ = H

Знайти: S_пов.  – ?

Розв’язок: . S_пов. = S_біч  +2S_осн

S_біч  =  Р_осн ∙ H; Р_осн  = 4а; S_біч  =  4а∙ H

S_осн = а²; 2S_осн =2а²

S_пов. = 4а∙ H +2а²