Розробка уроку на тему "Зображення фігур у стереометрії. Розв’язування задач"

Тема уроку.  Зображення фігур у стереометрії. Розв’язування вправ.

Мета уроку: формування вмінь будувати зображення просторових фігур,     розв’язування задач, використовуючи властивості паралельного проектування.

освітня: навчити виконувати наочні зображення за допомогою паралельного проектування; показати широке коло застосування властивостей паралельного проектування у навколишньому світі;

розвивальна: розвивати просторову уяву; логічне та аналітичне мислення;

виховна: виховувати акуратність при виконанні рисунків, розширювати загальний кругозір учнів, виховувати інтерес до вивчення даної теми та самостійність учнів

Методична мета уроку: формування вмінь та навичок будувати зображення просторових фігур при розв’язуванні задач шляхом практичного виконання  паралельного проектування.

Формування компетентностей:

✵ предметна компетентність: сформувати поняття про утворення паралельних проекцій основних фігур; сформувати вміння виконувати зображення просторових фігур на площині;

✵ ключові компетентності:

✵ спілкування державною мовою — доречно та коректно вживати в мовленні математичну термінологію;

✵ математична компетентність — оперувати геометричними ✵ соціальна та громадянська компетентності — висловлювати власну думку, слухати і чути інших;

✵ вміння вчитися впродовж життя.

Наскрізні лінії: підприємливість і фінансова грамотність.

Тип уроку: комбінований

Хід уроку

Епіграф уроку : «Серед рівних розумом за

однакових умов, переважає той,

хто знає геометрію»

Блез Паскаль

 

І. Організаційний етап.

Перевірка готовності здобувачів освіти до заняття.

“Світлофор”  Виявлення емоційного стану учнів перед уроком.

“ Виберіть смайлик, який відповідає вашому настрою на уроці”

 

ІІ. Перевірка домашнього завдання.

На дошці за готовим рисунком відтворюють домашню задачу.

 

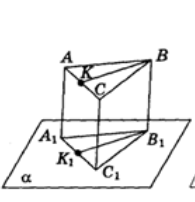
 Трикутник А₁В₁С₁ — паралельна проекція трикутника АВС на пло­щину α. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) якщо трикутник АВС правильний, то трикутник А₁В₁С₁ обов'яз­ково правильний (ні)

б) трикутник АВС не може дорівнювати трикутнику А₁В₁С₁  (ні)

в) якщо ВК — бісектриса трикутника АВС, то B₁K₁ обов'язко­во — бісектриса трикутника А₁В₁С₁ (ні)

г) якщо ВК — медіана трикутника АВС, то В₁К₁ обов'язково — медіана трикутника A₁B₁C₁(так)

 

III. Актуалізація опорних знань та вмінь

Вправа «Мозковий штурм»

1) Чи можуть нерівні відрізки мати рівні паралельні проекції? (так)

2) Чи можуть рівні відрізки мати нерівні паралельні проекції? (так)

3) Чи може довжина паралельної проекції відрізка бути більшою від довжини цього відрізка? (так)

4) Які геометричні фігури можуть бути паралельними проекціями:

а) точки; б) відрізка; в) променя; г) прямої; д) двох паралельних відрізків; е) двох паралельних прямих; ж) двох прямих, що перетинаються; з) двох мимобіжних прямих

5) Проекції прямих а і b на площину паралельні. Як розміщені прямі a і b?      (паралельні)

6) Чи можуть дві прямі, що перетинаються, проектуватися:

а) у дві прямі, що перетинаються;(так)

б) у паралельні прямі;(ні)

 в) у пряму і точку на ній;(так)

 г) у пряму і точку поза нею?(ні)

7) Чи зберігаються відношення відрізків при паралельному проектуванні? (так)

ІV. Закріплення та осмислення знань учнів .

Формування вмінь будувати зображення фігур

Зупинимося на зображенні найбільше вживаних геометричних фі­гур, з комбінацій яких складається, як правило, зображення будь-якої складної просторової фігури.

1.     ЗОБРАЖЕННЯ ТРИКУТНИКА

Будь-який трикутник може бути зображенням трикутника довільної форми, зокрема: правильного, рівнобедреного, прямокутного.

 

Слід зазначити, що медіани і середні лінії трикутника зображають відповідно медіанами і середніми лініями зображення.

 

Задача 1.

На зображенні рівностороннього трикутника побудуйте зображення його центра.

Розв'язання.

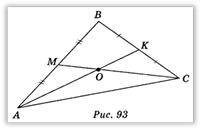
Нехай АВС (рис. 93) — дане зображення рівностороннього трикут­ника. Центр правильного трикутника — точка перетину його медіан. Тому, побудувавши медіани АК і CM на зображенні, які перетнуться в точці О, одержимо: точка О — центр правильного трикутника АВС.

 

2.     ЗОБРАЖЕННЯ ПАРАЛЕЛОГРАМА

Зображенням паралелограма (прямокутни­ка, ромба, квадрата) можна вважати довільний паралелограм, що належить площині проекцій.

Задача 2.

Побудуйте зображення ромба з кутом 120° та зображення висоти ромба, яку проведено з вершини цього кута.

Розв'язання

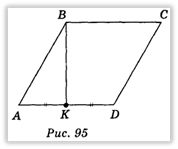Нехай паралелограм ABCD (рис. 95) є зображенням ромба A₁B₁C₁D₁, у якого <B₁ = 120° (рис. 96).

Оскільки ΔА₁В₁D₁ — рівносторонній, то його медіана В₁K₁ є одно­часно і висотою цього трикутника, а отже, і ромба.

Таким чином, побудувавши середину сторони AD і з'єднавши цю точку з вершиною В, одержимо 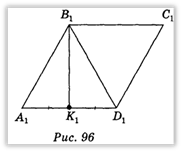ВК — зображення висоти (див. рис. 95).

 

 

 

 

 

 

 

 

 

3.     ЗОБРАЖЕННЯ ТРАПЕЦІЇ

Зображен­ням трапеції є трапеція, у якій відношення довжин основ зображення дорівнює відношенню довжин основ трапеції, яку проектують.

Задача.

Побудуйте зображення рівнобічної трапеції з основами 3 і 9 см та зображення її висоти.

     Розв'язання

Нехай A₁B₁C₁D₁ — рівнобічна трапеція, у якій 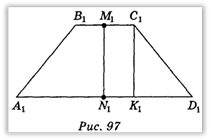А₁D₁ || В₁С₁, A₁D₁ = 9 см, В₁С₁ = 3 см. Слід зазначити, що висота С₁К₁ паралельна осі симетрії М₁N₁ (точки М₁ і N₁ — середини основ трапеції) (рис. 97). Але при паралельному проектуванні зберігаються паралельність прямих і відно­шення довжин паралельних відрізків. Звідси випливає побудова: трапе­ція ABCD, у якій        AD || ВС і AD = 3 ВС , є 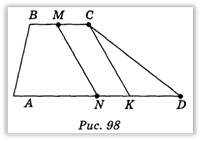зображенням трапеції (рис. 98); побудувавши точки М і N — середини сторін ВС і AD і СК ||  MN, одер­жимо відрізок СК — зображення висоти трапеції.

 

 

 

 

4.     ЗОБРАЖЕННЯ ЧОТИРИКУТНИКА

Зображенням довільного чотирикутника (не паралелограма і не тра­пеції) є довільний чотирикутник.

 

5.     ЗОБРАЖЕННЯ КОЛА

Зображенням кола з центром в точ­ці О₁ є еліпc з центром в точці О, який належить площині проекції α. Кожний 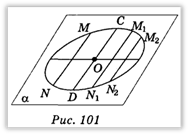діаметр еліпса АВ ділить пополам хорди MN, M₁N₁, M₂N₂ ..., паралельні до спря­женого з ним діаметра CD (рис. 101).

Слід зазначити, що спряженими ді­аметрами еліпса називаються зобра­ження двох перпендикулярних діаме­трів кола, що проектується.

 

 

V. Підведення підсумку уроку.

• На сьогоднішньому занятті я зрозумів /дізнався/розібрався...
• Я хочу похвалити себе за те, що на сьогоднішньому занятті ...
• На занятті мені особливо сподобалося ...
• Знання із сьогоднішнього заняття мені знадобляться ...
• На сьогоднішньому уроці мене здивувало ...

VІI.  Домашнє завдання.

§ 4, п.32. Задача №32.13.  Виконати тести за посиланням.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку.  Зображення фігур у стереометрії. Розв’язування вправ.

Мета уроку: формування вмінь будувати зображення просторових фігур,     розв’язування задач, використовуючи властивості паралельного проектування.

освітня: навчити виконувати наочні зображення за допомогою паралельного проектування; показати широке коло застосування властивостей паралельного проектування у навколишньому світі;

розвивальна: розвивати просторову уяву; логічне та аналітичне мислення;

виховна: виховувати акуратність при виконанні рисунків, розширювати загальний кругозір учнів, виховувати інтерес до вивчення даної теми та самостійність учнів

Методична мета уроку: формування вмінь та навичок будувати зображення просторових фігур при розв’язуванні задач шляхом практичного виконання  паралельного проектування.

Формування компетентностей:

✵ предметна компетентність: сформувати поняття про утворення паралельних проекцій основних фігур; сформувати вміння виконувати зображення просторових фігур на площині;

✵ ключові компетентності:

✵ спілкування державною мовою — доречно та коректно вживати в мовленні математичну термінологію;

✵ математична компетентність — оперувати геометричними ✵ соціальна та громадянська компетентності — висловлювати власну думку, слухати і чути інших;

✵ вміння вчитися впродовж життя.

Наскрізні лінії: підприємливість і фінансова грамотність.

Тип уроку: комбінований

Хід уроку

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

    Розв’язання задачі на дошці за готовим малюнком.

 

     III. Актуалізація опорних знань та вмінь.

         Вправа «Мозковий штурм».

     ІV. Мотивація навчальної діяльності.

     V. Закріплення та систематизація знань здобувачів освіти.

          Розв'язування задач.

VІ. Підведення підсумку уроку.

VІІ.  Домашнє завдання.

§ 4, п.32. Задача №32.13.  Тести  за посиланням.