Розробка уроку "Рівняння та його корені"
Урок № 3.
Мета: домогтися свiдомого сприйняття змiсту поняття «рiвняння»; поглибити, розширити та узагальнити знання учнiв про рiвняння, здобутi в молодших класах.
Тип уроку: узагальнення та систематизація знань.
Хiд уроку
І. Органiзацiйний момент
Інструктаж учителя щодо ходу проведення уроку.
ІІ. Перевiрка домашнього завдання
Перевiрку виконання основної частини домашнього завдання (завдання на вiдтворення можна провести у формi заповнення анкети:
№ прикладу: ... вiдповiдь: ... вид перетворення: ... — зiбрати на перевiрку (оцiнка може бути вербальною) або зiбрати зошити, перевiрити ретельно домашнє завдання i оцiнити як домашню самостiйну роботу.
Завдання № 2 є завданням випереджального характеру, тому на його перевiрку вiдводиться бiльше часу на уроцi.
ІІІ. Робота iз випереджальним домашнiм завданням
На дошцi записане завдання № 2 з домашнього завдання:
Серед математичних записiв один зайвий. Пояснiть, який та чому?
-
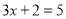 ; 2)
; 2)  ; 3)
; 3) 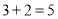 ; 4)
; 4) 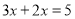 .
.
Кожний з учнiв отримує завдання здiйснити порiвняння за алгоритмом:
- знайдiть вiдмiнностi мiж цими записами;
- знайдiть схожiсть у цих записах;
- сформуйте групи за ознакою схожостi;
- дайте означення утвореним групам.
* Якщо дiти не володiють термiнологiєю, то варто попрацювати над тлумаченням слова «визначити» (додаток): скiльки має лексичних значень; як адаптується на математичному розумiннi; яке смислове порiвняння, не пов’язане з математикою, могли б дати цьому поняттю (наприклад, «означення» — це як портрет поняття, що визначається).
У будь-якому разi пiсля проведеної роботи учнi усвiдомлюють, що рiвнiстю з невiдомим значенням букви називають рiвняння з одним невiдомим (або рiвняння з однiєю змiнною).
Оскiльки з рiвняннями учнi уже зустрiчались у молодших класах, їм знайомi поняття «рiвняння», «корiнь рiвняння», вони взагалi розумiють змiст завдання — розв’язати рiвняння. На уроцi цi вiдомостi систематизуються, узагальнюються та поглиблюються, а саме:
- звертаємо увагу на те, що традицiйно пiсля нестрогого означення рiвняння з однiєю змiнною формулюється означення кореня (розв’язку рiвняння), у зв’язку з чим:
- звертаємо увагу учнiв на той факт, що рiвняння з однiєю змiнною може мати один або кiлька, або безлiч коренiв, а може й не мати їх взагалi, а тому:
- завдання щодо розв’язування рiвняння вважатиметься вiдтепер виконаним, якщо знайдено всi коренi або доведено, що їх взагалi не iснує.
Зауважимо, що сприйняття учнями 2-ї частини теоретичного матерiалу є найбiльш проблемним, тому бажано в ходi пояснення спиратись на конкретнi текстовi задачi. Наприклад:
Задача 1. Якщо невідоме число збільшити у 3 рази, дістанемо 18. Знайдіть невідоме число.
Розв’язання. Нехай ![]() - невідоме;
- невідоме; ![]() - рівняння; 6 – корінь, єдиний.
- рівняння; 6 – корінь, єдиний.
Задача 2. Добуток трьох послідовних цілих чисел дорівнює 0. Знайдіть ці числа.
Розв’язання. Нехай ![]() - менше число, тоді
- менше число, тоді ![]() та
та ![]() наступні цілі числа, добуток яких
наступні цілі числа, добуток яких ![]() дорівнює 0. Маємо рівняння:
дорівнює 0. Маємо рівняння: ![]() його розв’язки знаходимо з умов:
його розв’язки знаходимо з умов:
![]() або
або ![]() ; або
; або ![]() ,
,
![]()
![]() .
.
Отже, або ![]() ,
, ![]() ;
; ![]() , тобто числа 0; 1; 2;
, тобто числа 0; 1; 2;
або ![]() ,
, ![]() ;
; ![]() , тобто числа -1; 0; 1;
, тобто числа -1; 0; 1;
або ![]() ,
, ![]() ;
; ![]() , тобто числа -2; -1; 0.
, тобто числа -2; -1; 0.
Задача має три розв’язки!!!
Задача 3. На одному шальку терезів поклали п’ять однакових гир, а на другому спочатку дві, а потім ще три таких самих гир, після чого терези врівноважилися. Яка маса гирі?
Розв’язання. Нехай маса однієї гирі ![]() кг, тоді маса двох -
кг, тоді маса двох - ![]() кг, трьох -
кг, трьох - ![]() кг, п’яти -
кг, п’яти - ![]() кг. Складемо рівняння:
кг. Складемо рівняння: ![]() .
.
Знаходимо, що ![]() , тобто
, тобто ![]() може бути будь-яким додатним числом (бо за змістом задачі
може бути будь-яким додатним числом (бо за змістом задачі ![]() - маса – не може бути ані 0, ані від’ємним числом).
- маса – не може бути ані 0, ані від’ємним числом).
Отже, задача має безліч розв’язків.
Задача 4. Невідоме число збільшили на 3 і дістали те ж саме силос. Яке число задумали?
Розв’язання. Нехай ![]() - невідоме число. За умовою задачі
- невідоме число. За умовою задачі ![]() , але такого числа, щоб було менше за самого себе, не існує, тобто рівняння не має коренів.
, але такого числа, щоб було менше за самого себе, не існує, тобто рівняння не має коренів.
V. Закрiплення знань. Засвоєння вмiнь
Важливим видом завдань, якi повиннi навчитися розв’язувати учнi, є такi:
а) перевiрка, чи є число коренем рiвняння;
б) складання рiвнянь iз заданими коренями;
в) розв’язування рiвнянь, що мають кiлька коренiв (за властивiстю 0 при множеннi), та рiвнянь, що мають безлiч коренiв або не мають коренiв.
-
Чи є числа 2; -1; 0; 1; 2 коренем рівняння
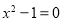 ?
?
- Скільки коренів мають рівняння?
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
-
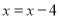 ; 2)
; 2) 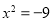 ; 3)
; 3) 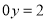 ; 4)
; 4) 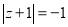 .
.
-
Розв’яжіть рівняння:
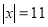 ;
; 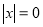 ;
; 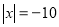 .
.
-
Чи є число 3 коренем рівняння?
-
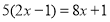 ; 2)
; 2) 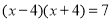 ; 3
; 3 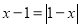 .
.
-
- Які з чисел -2; -1; 0; 2; 3 є коренями рівняння?
1) ![]() ; 2)
; 2) ![]() .
.
1) кожне з чисел 7; –3 та 0 є коренем рiвняння; ![]()
2) коренем рівняння ![]() y є будь-яке число;
y є будь-яке число;
3) рiвняння ![]() не має коренiв.
не має коренiв.
4. Складiть яке-небудь рiвняння, коренем якого є число: 1) 8; 2) –12.
5*. При яких значеннях коефiцiєнта ![]() рiвняння
рiвняння ![]() має єдиний корiнь? Чи iснує таке значення
має єдиний корiнь? Чи iснує таке значення ![]() , при якому це рiвняння не матиме коренiв; буде мати безлiч коренiв?
, при якому це рiвняння не матиме коренiв; буде мати безлiч коренiв?
6*. При яких значеннях коефiцiєнта ![]() рiвняння
рiвняння ![]() має корiнь, що дорiвнює: –5; 1; 20?
має корiнь, що дорiвнює: –5; 1; 20?
Учень 7 класу Петрик Тяпляпкін, розв’язавши завдання «Чи є число 2 коренем рівняння ![]() ?» і отримавши ствердну відповідь, зробив висновок, що він розв’язав це рівняння. Чи правильний висновок зробив Петрик? Чому?
?» і отримавши ствердну відповідь, зробив висновок, що він розв’язав це рівняння. Чи правильний висновок зробив Петрик? Чому?
VII. Домашнє завдання
№ 1. Чи є коренем рівняння ![]() числа: 1) 2; 2) 0; 3) –1; 4) 4; 5) 3?
числа: 1) 2; 2) 0; 3) –1; 4) 4; 5) 3?
№ 2. Запишіть рівняння, що має:
1) єдиний корінь — число 4;
2) два корені 4 та –4.
№ 3. При яких значеннях ![]() коренем рівняння
коренем рівняння ![]() є число 1?
є число 1?
№ 4. Випереджальне домашнє завдання
Розгляньте розв’язання рівняння:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Використовуючи текст підручника, поясніть, на підставі яких властивостей (тверджень) виконано кожний крок у розв’язанні цього рівняння.
Додаток
Визначати за тлумачним словником:
1) з точністю з’ясувати, встановити;
2) розкрити словами зміст будь-чого;
3) назначити з будь-якою метою;
4) намітити для виконання.
Визначати завдання на майбутнє.
Определять (рос.)


про публікацію авторської розробки
Додати розробку
