Розробка відкритого уроку з математики для 5 класу на тему "Додавання і віднімання десяткових дробів"

Тема: Додавання і віднімання десяткових дробів

Мета:

Навчальна: встановити загальні правила додавання і віднімання десяткових дробів, формувати вміння застосовувати ці знання на практиці. Продовжити роботу по формуванню стійкого інтересу до математики; активізувати пізнавальну діяльність учнів;

Розвивальна: розвивати творчі здібності учнів (уяву, спостережливість, пам’ять, мислення);

Виховна: створити умови для відносин співпраці між учнями; формувати відчуття відповідальності за доручену роботу, уміння слухати і чути; прищеплювати навички роботи з додатковими джерелами інформації.

Тип уроку:  засвоєння нових знань, формування вмінь і навичок.

Обладнання та наочність: дошка, комп’ютер, навчальна комп’ютерна презентація, картки з рефлексією, картки з відповідями, картки із завданнями, картки  з кросвордом, картки емоційного стану.

 

Хід  уроку

Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати.

Д. Пойа

Мозок, добре впорядкований, вартий більше, ніж добре наповнений.

М. Монтель

І.Організаційний момент.

Учитель  пропонує сісти . Черговий учень доповідає хто відсутній на уроці, а потім  просить всіх підняти з парт рефлексію готовності до уроку.

 

 

 

 

 

 

 

ІІ. Актуалізація опорних знань

Учитель.

Отже, всі готові до уроку, можемо починати. Давайте  з вами повторимо. Увага на екран:

• Чи однакові десяткові дроби 2,3000; 2,300; 2,30 і 2,3?
• Як записати будь-яке натуральне число десятковим дробом?
• Чи можна записати число півтора?
• Як називаються закони додавання: a+b = b+a , a + (b+c) = (a+b) + c ?

 

ІІІ. Ознайомлення з темою і метою уроку

Учитель.

 На сьогоднішньому уроці  нас чекають цікаві завдання. Хочу зауважити, що в роботі нам допоможе вислів  давньогрецького філософа і вченого Аристотеля «Розум полягає не лише в знаннях, але й у вмінні застосовувати ці знання» і відомого математика Дьордь. Пойа: «Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати»

Дорогі діти! У казковій країні Знань є міста з дивними назвами: Українська мова, Історія, Образотворче мистецтво та інші малі та великі міста. Серед них і місто Математика. Тут ви буваєте часто. У цьому місті є широкі просторі вулиці з незвичними назвами, казкові будинки, храми,  величезні загадкові замки. Наприклад, найвеличніший стародавній храм, у якому ви часто буваєте, називається Таблиця множення.

У місті Математика є дуже довга вулиця – вулиця Натуральних чисел. Недавно ви потрапили на нову вулицю – вулицю Дробових чисел. На цій вулиці мешкають Звичайні дроби. Це дуже дивні чоловіки двох видів: в одних голова більша за тулуб, в інших – навпаки. А серед них є диваки, які можуть перевтілюватись, їх називають Десяткові дроби. Ви подружилися з ними і тепер разом сміливо заходите у кожний будинок вулиці Дробових чисел. Сьогодні завітаєте до будинку під вивіскою “Додавання та віднімання десяткових дробів”. 

 

ІІІ. Мотивація навчальної діяльності       

Давайте трішки «пірнемо в минуле», і послухаємо історію виникнення дробів, а допоможуть нам «Мандрівники в минуле»

Іще в Давньому Єгипті люди використовували дроби. Спочатку всі дроби, які використовували єгиптяни, мали в чисельнику одиницю. Окремі дроби мали спеціальні назви. Наприклад: половина, третина, четвертина, десятина.

У стародавній Русі дроби називали «частками», а згодом «ламаними числами».

Десяткові дроби, як і звичайні, виникли з потреб практики. Ще в ІІ столітті до нашої ери в деяких країнах застосовувалась десяткова система мір довжини. Десяткова лічба поширилась на міри ваги й об’єму. Тому постало питання про спрощення дій з дробами.

Першим ввів поняття десяткового дробу і визначив правила дій з десятковими дробами видатний математик  Ал-Каші в своїй праці «Ключ до арифметики». (1427 р.)

Але в Європі відкриття ал-Каші стали відомими лише через 300 років. Нічого не знаючи про відкриття ал-Каші, десяткові дроби удруге відкрив, приблизно через 150 років після нього, математик Симон Стевін.

Відокремлювати цілу частину десяткового дробу від дробової частини пропонували по різному. Ал-Каші пропонував писати цілу і дробову частини різними чорнилами. Пізніше ставили між цілою і дробовою частинами вертикальну риску. Стевін запропонував писати кружечки,наприклад 35,9 – 35_о9.

Прийняту  в наш час кому, запропонував в 17 столітті німецький математик і астроном Йоган Кеплер (1571 —1630).

 

Ігрова ситуація

Уявіть ситуацію: два учні діляться  шоколадкою. Одну шоколадку поділили на десять частин. Один учень взяв 3 частинки, а інший 4 частинки. Скільки частинок вони з’їли разом? 

Скільки залишилося?  

На скільки більше один з’їв за іншого? 

А тепер якщо це перетворити у десяткові дроби:

0,3+0,4=0,7

1-0,7=0,3

0,4-0,3=0,1

Проблема: Скільки буде, якщо 0,4+0,03? Як  це зробити?

Учитель.

Отже, ми розпочнемо міркувати, як це зробити.

 

IV.  Пояснення нового матеріалу.

Учитель.

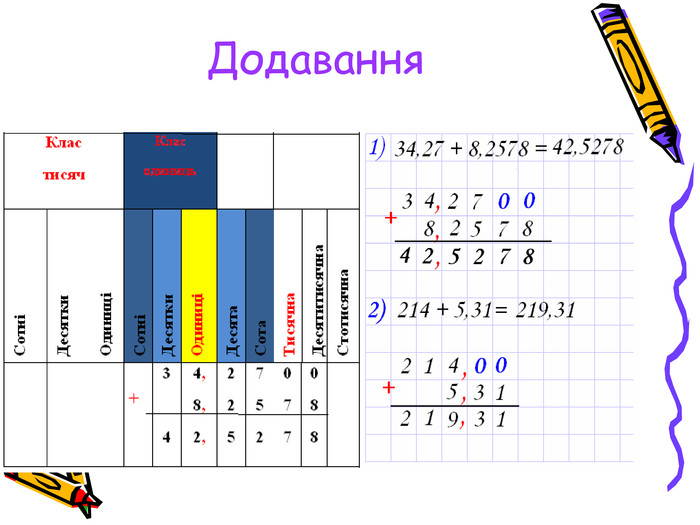
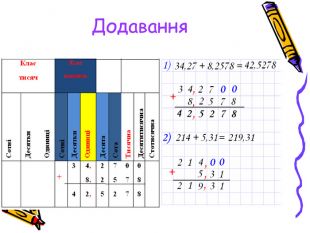
Отже, додавання десяткових дробів можна звести до додавання натуральних чисел.

0,78+0,21=0,99

0,3+0,4=0,7

Якщо треба додати дроби з різною кількістю цифр після коми, то спочатку треба зрівняти цю кількість цифр, приписавши праворуч до одного з чисел стільки нулів, скільки потрібно. Наприклад:

0,4+0,03=0,40+0,03=0,43

7,6+11,35=7,60+11,35=18,95

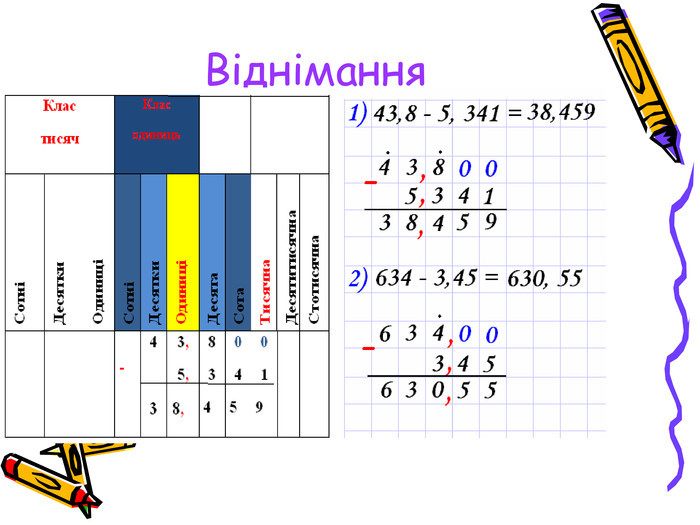
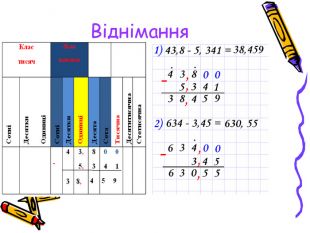
Зрозуміло, що «у стовпчик» можна додавати і віднімати десяткові дроби так як натуральні числа. При цьому треба пам’ятати, що кому треба ставити під комою.

Алгоритми додавання і віднімання десяткових дробів

1.                Зрівняй кількість цифр після коми в обох числах.
2.                Запиши у стовпчик, щоб кома знаходилась під комою; додавай і віднімай як натуральні числа.
3.                Постав кому в сумі чи різниці під комою в даних числах.

V.  Застосування знань. Формування вмінь

 Завдання 1.

 Вправа «Виправ помилку» (По черзі учні виходять до дошки виправляють, а потім звіряємося)

1. 52 + 18 = 7;                 
2.  736 – 336 = 4;
3. 3 + 108 = 408;
4. 74 – 24 = 5;
5. 73 + 27 = 10;
6. 57 – 4 = 17;

Відповіді:

•  52 + 18 = 7;       (5,2 + 1,8 = 7)
• 736 – 336 = 4;   (7,36 – 3,36 = 4)
• 3 + 108 = 408;     (3 + 1,08 = 4,08)
• 74 – 24 = 5;       (7,4 – 2,4 = 5)
• 73 + 27 = 10;    (7,3 +2,7 = 10)
• 57 – 4 = 17;       (5,7 – 4 = 1,7)

 Фізкультхвилинка

 Встаньте, діти, посміхніться,

Землі нашій уклоніться

За щасливий день вчорашній.

Всі до сонця потягніться,

Вліво, вправо нахиліться,

Веретенцем покрутіться.

Раз присядьте, два присядьте

І за парти тихо сядьте.

Завдання 2. 

Математичне лото

Обчисліть, використовуючи прийоми швидкого обчислення:

1. 0,8-0,1; 4) 9,43- 5,43; 7)13,5-13;
2. 12,7-0,7; 5) 43,8- 3,8;  8) 6,05-3,05;
3. 3,48-3,44; 6) 8- 0,5;  9) 36-0,6

 

Учні виконують завдання, а потім вибирають правильні відповіді з карток прикріплених на дошці зі списку, де є правильні і неправильні відповіді. Учень, який знайшов правильну відповідь виходить до дошки і прикріплює картку до квадрату з таким же числом, як і номер завдання. Якщо всі завдання виконані правильно, то на зворотній стороні отримаємо  картинку.

1 0,7	4 4	7 0,5
2 12	5 40	8 3
3 0,04	6 7,5	9 35,4

 

                                    

Учитель. Перед вами зображення дерева, яке цікаве тим, що воно, являється найвищим у світі.Завдання 3.

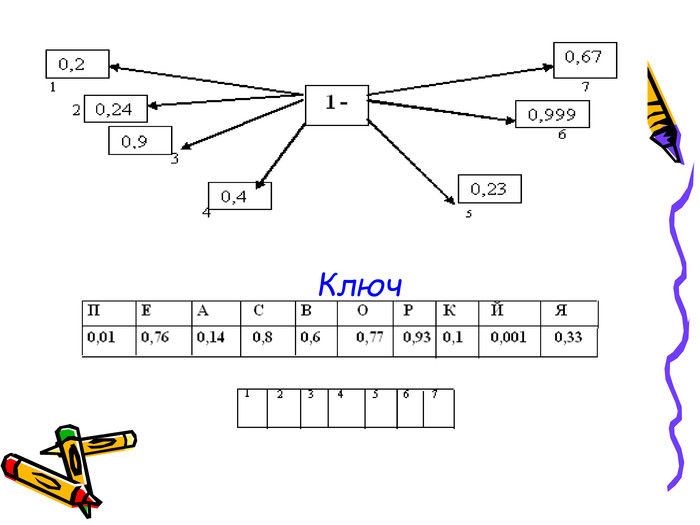
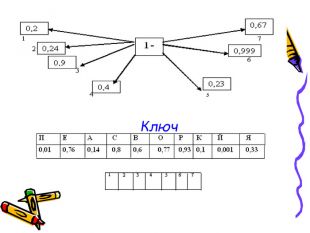
Розгадай слово

Визначте назву найвищого дерева у світі, виконавши завдання за схемою. (Виконання вправи відбувається у невеликих групах)

 

 

 

1  7

    2 

   6

 3 

 

                                 4               5

Ключ

П	Е	А	С	В	О	Р	К	Й	Я
0,01	0,76	0,14	0,8	0,6	0,77	0,93	0,1	0,001	0,33

 

1

2

3

4

5

6

7

Відповідь: Секвойя

Учитель. Це незвичайне дерево, відноситься до родини кипарисових, а росте  до шести тисяч років. Але мабуть у вас виникає цікавість,  а якої, ж висоти виростає це дерево? Давайте дізнаємося, розгадавши наступне завдання

Завдання 4.

Розв’яжіть рівняння

(x-51,2)+25,3=84,1

Відповідь. 110м.

Учитель.

Розв’яжіть кроссворд і дізнайтесь, на узбережжі якого океану росте секвойя (учні розв’язують у групах).

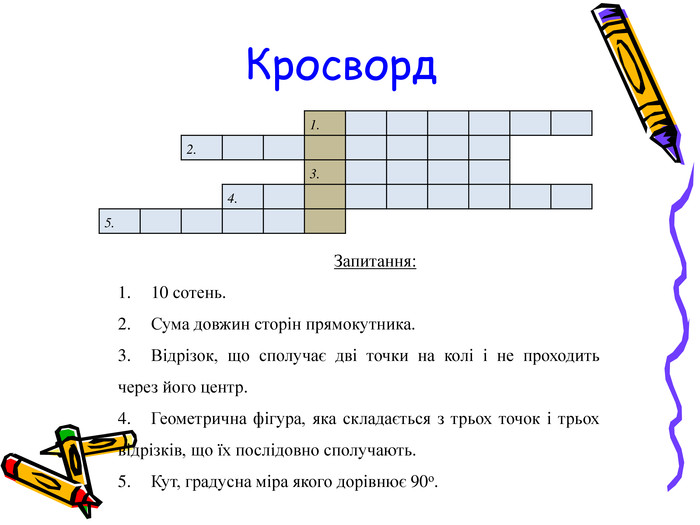
Завдання 5. Розв’яжіть кросворд

					1.
		2.
					3.
			4.
5.

 

Запитання:

1.                10 сотень.
2.                Сума довжин сторін прямокутника.
3.                Відрізок, що сполучає дві точки на колі і не проходить через його центр.
4.                Геометрична фігура, яка складається з трьох точок і трьох відрізків, що їх послідовно сполучають.
5.                Кут, градусна міра якого дорівнює 90^о.

Відповідь. Тихий.

Учитель.

 Окрім того, що це дерево  найвище в світі, воно має ще одну цікаву характеристику: спили величезних стовбурів гігантського дерева секвої досягають 12 метрів у поперечнику. У тунель, зроблений в такому дереві, вільно в'їжджає екіпаж, а на пні можуть танцювати шістнадцять пар і поміщається оркестр (фото на слайдах).

 

6.  Закріплення матеріалу

 

•                  Що ми робили на уроці?
•                  Про що дізналися?
•                  Як додавати десяткові дроби?
•                  Сформулюйте  алгоритм додавання десяткових дробів.

 

7. Підбиття підсумків уроку.

 

Наприкінці уроку учні заповнюють картки емоційного стану – картки настрою. Для діагностики використовують картки, в яких учні відмічають своє самопочуття, вказують своє ставлення до уроку, вписуючи те, що сподобалося (не сподобалось) на уроці.

 Виставлення оцінок.

VIII. Домашнє завдання (згідно з підручником)

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

 

1. Істер О.С.  Математика (підручник 5 клас). – К. : Генеза, 2013.

 

2. Мерзляк А. Г., Полонський В. Б., Якір М. С.  Математика (підручник 5 клас). – К. : Гімназія, 2013.

 

3. Апостолова Г. В., Бакал О. П. Логічними стежинками математики (5-9 класи). – К. : Генеза, 2013.

 

4. Істер О. С., Баришнікова О. І., Карликова О. А. Навчально-методичний посібник «Математика. Книжка для вчителя». – К. : Генеза, 2013.

Інтернет-ресурси

5. HTTP: //uk.wikipedia.org