Розв’язування ірраціональних рівнянь та їх систем.

Тема: Розв’язування ірраціональних рівнянь та їх систем.

Навчальна мета: узагальнити знання студентів з теми, вдосконалити вміння розв’язувати ірраціональні рівняння та їх системи.

Розвиваюча мета: розвивати логічне мислення студентів, увагу, пам'ять, мову, навички колективної та самостійної роботи.

Виховна мета: виховувати доброзичливість, старанність, дисциплінованість, відповідальність, культуру математичних записів, інтерес до математики.

Очікувані результати: Після заняття студенти зможуть:

• Удосконалити свої вміння і навички розв’язування ірраціональні рівняння та їх системи;
• Набути навичок творчого мислення;
• Розвинути вміння робити вибір, приймати рішення, брати на себе відповідальність і безконфліктно спілкуватися в колективі.

Тип заняття: практичне заняття.

Форма навчання: індивідуально – групова.

Обладнання: мультимедійне обладнання, презентація вчителя, лист для оцінювання, роздатковий матеріал.

Епіграф: «Для того щоб удосконалити розум, треба більше розмірковувати, ніж заучувати» (Рене Декарт — французький філософ і математик.)

Література:

1. Нелін Є.П. Алгебра і початки аналізу: підруч. для 10 кл. загальноосвіт. навчальн. закладів: академ. рівень – Х.: Гімназія, 2010. – 416 с.

2. Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002.

3. Збірник завдань для державної підсумкової атестації з математики., 11 клас: У 2 кн. Кн..2/ М.І. Бурда, О.Я. Біляніна та ін., - Х.: Гімназія, 2008.

4. Тиждень математики в школі. 5-11 класи/ Т.Л.Корнієнко, В.І.Фіготіна. – 3-тє вид. – Х.:Веста, 2010.

План заняття:

№п/п	Назва етапу заняття	Час	Метод проведення
1.	Організаційний момент. Створення емоційного настрою.	3 хв.	«Обмін думками»
2.	Перевірка домашнього завдання.	5 хв.	Самоперевірка за зразком
3.	Актуалізація опорних знань.	5 хв.	«Інтелектуальна розминка»
4.	Закріплення та відпрацювання умінь і навичок.	45хв. 15хв.	1. «Коло ідей» 2. Тестування з подальшою взаємоперевіркою
5.	Домашнє завдання.	2 хв.	Звернення до групи
6.	Підсумок заняття. Виставлення оцінок.	5 хв.	Рефлексивна бесіда

 

ХІД ЗАНЯТТЯ:

I. Організаційний момент. Створення емоційного настрою.

Привітання, перевірка присутніх, перевірка готовності групи до заняття. Обговорення епіграфу до заняття.

Технологія особистісно орієнтованого навчання «Обмін думками»

 – Зверніть увагу на епіграф заняття. Як ви розумієте ці слова?

Оголошення теми та визначення очікуваних результатів заняття.

Студенти поділені на чотири групи, в кожній групі обрано голову групи, яка буде організовувати роботу всієї групи, оцінювати кожного члена групи.

Роботу на занятті оцінюється за допомогою листа оцінювання. Кожен етап заняття оцінюється певною кількістю балів.

ІІ. Перевірка домашнього завдання.

Самоперевірка за зразком (розв’язання вправ роздається кожному студентові).

– Оскільки ми з вами працюємо на довірі, то я пропоную кожному з вас самостійно перевірити домашнє завдання за зразком і виставити відповідні бали. Голова групи виставляє відповідні бали в лист оцінювання кожному студентові.

Правильне виконане завдання –  0,5 бали

Неправильно виконане завдання – 0 балів.

Максимальна кількість балів за даний етап – 2 бали.

Розв’язати рівняння:

а)

Розв’язання:;

;

;

;

;

;

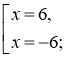
Відповідь: .

б) ;

Розв’язання: ;

;

;

;

;

Так як ;

, тоді , .

Перевірка: , ;

;

, ;

, отже – сторонній корінь

Відповідь: 3.

в);

Розв’язання: ;

Оскільки , а то рівність неможлива при жодних дійсних значеннях змінної .

Відповідь: коренів немає.

г) Розв’язати рівняння:;

Розв’язання: ;

  Нехай , , тоді ;

  Маємо ;

Так як ;

, тоді , .

Обернена заміна:  і ;

,  

,  

Відповідь: .

ІІІ. Актуалізація опорних знань.

«Інтелектуальна розминка»

Кожній групі, по черзі, ставиться 2 запитання, якщо група відповідає правильно на обидва запитання, то кожен член групи отримує по 1 балу, на одне запитання – 0,5 бали, жодної правильної відповіді – нуль балів.

1. Рівність, яка містить невідомі числа, позначені буквами називається ….(рівнянням).

2. Значення змінної, при якому рівняння перетворюється на вірну числову рівність  називається ….( коренем рівняння).

3. Розв’язати рівняння означає …….(знайти усі його корені або довести,  що їх немає).

4. Ірраціональним рівнянням називається…..(рівняння, що містить змінну під знаком кореня. ).

5. Розв’язування ірраціональних рівнянь ґрунтується на зведенні заданого рівняння …. (за допомогою деяких перетворень до раціонального).

6. Основними методами розв’язування ірраціональних рівнянь є … (піднесення обох частин рівняння до одного і того  самого степеня; заміна змінної; використання властивостей функцій).

7. При піднесені обох частин рівняння до непарного степеня завжди отримуємо …. (рівняння, рівносильне даному).

8. При піднесені обох частин рівняння до парного степеня можуть з’явитися … (сторонні корені), які відсіюються … (перевіркою)?

ІV. Закріплення та відпрацювання умінь і навичок.

1. «Коло ідей»

Ми згадали теорію, тож  переходимо до практики.

Пам’ятаєте легенду про те, як великий Архімед біг по вулиці і кричав «Еврика!». Його тоді так захопила нова ідея, що він і не помітив, що вискочивши з ванни, забув одягтися. Справді, коли нас осяває якась ідея, особливо, якщо це розв’язання якоїсь проблеми, що давно не дає спокою, ми відчуваємо почуття радості, піднесення, гордості.

Звичайно, ідеї, які нехай сьогодні осяють вас, не можна назвати великими, але пам’ятайте – велике починається з малого.

Працюємо під девізом:

Думаємо колективно,

Працюємо оперативно,

Сперечаємося доказово –

Це для всіх обов’язково.

Технологія особистісно розвивального навчання «Коло ідей»

Групи отримують однакове завдання (висвічується на слайді). Спочатку протягом 1 хвилини студенти обговорюють завдання, потім група, яка перша знайшла шлях розв’язання вигукує «Ідея!» і пропонує свій спосіб розв’язування завдання. Ідея обговорюється, коментується і, можливо, доповнюється. Завдання розв’язується на дошці. Після розв’язання чотирьох завдань, голова групи оцінює активність роботи кожного студента в групі. Відповідно від їх активності, виставляє кожному членові групи від нуля до чотирьох балів.

Зразки завдань:

1. Розв’яжіть рівняння ;

Розв’язання: ;

;

;

;

;

.

Відповідь: .

2. Розв’яжіть рівняння ;

Розв’язання: Ізолюємо один корінь і піднесемо обидві частини рівняння до квадрата – таким чином ми позбудемося одного кореня.

;

;

;

;

Знову ізолюємо корінь і знову піднесемо обидві частини рівняння до квадрата – внаслідок одержимо квадратне рівняння.

;

;

;

;

;

;

, .

Оскільки при піднесенні до квадрата можна одержати сторонні корені, то в кінці виконуємо перевірку отриманих коренів.

Перевірка: , ;

; отже – корінь даного рівняння

  , ;

    ; отже – сторонній корінь.

Відповідь: .

3. Розв’яжіть рівняння ;

Розв’язання: ;

  Нехай , , тоді ;

  Маємо ;

Так як ;

, тоді , –  не задовольняє умову заміни

.

Обернена заміна: ;

,

.

Відповідь: .

4. Розв’яжіть систему рівнянь:

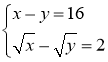
Розв’язання.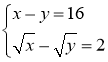

Введемо нові змінні і тоді система прийме вигляд:

,  

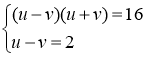
Підставимо у перше рівняння системи , матимемо систему рівнянь рівносильну заданій:              .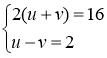

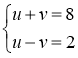Розв’яжемо систему рівнянь способом додавання:

  

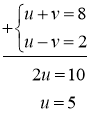
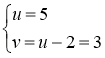
Повертаючись до початкових невідомих, матимемо:

,   

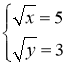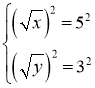
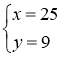
Відповідь:.

2) Тестування з подальшою взаємоперевіркою

Виконання тестових завдань студентами 5 хвилин. Потім один студент записує відповіді на дошці. Всі інші обмінюються варіантами і виконують взаємоперевірку оцінюючи кожне правильно виконане завдання по 1 балу.

Максимальна кількість балів – 5

Варіант 1

1.  Вказати рівняння, яке не має коренів:

А	Б	В	Г	Д

2. Скільки коренів має рівняння ?

А	Б	В	Г	Д
Жодного	Тільки один	Тільки два	Безліч	Визначити неможливо

3. Розв’яжіть рівняння: .

А	Б	В	Г	Д
				інша відповідь

4. Розв’яжіть рівняння: .

А	Б	В	Г	Д
				інша відповідь

 5. Установіть відповідність між поданими рівняннями та їх розв’язками:

 1) ;   А) ;

 2) ;  Б) ;

 3) ;  В) ;

 4) ;   Г) ;

      Д) .

Варіант 2

1.  Вказати рівняння, яке не має коренів:

А	Б	В	Г	Д

2. Скільки коренів має рівняння ?

А	Б	В	Г	Д
Жодного;	Тільки один	Тільки два	Безліч	Визначити неможливо

3. Розв’яжіть рівняння:   

А	Б	В	Г	Д
				інша відповідь

4. Розв’яжіть рівняння:

А	Б	В	Г	Д
				інша відповідь

5. Установіть відповідність між поданими рівняннями та їх розв’язками:

 1) ;   А) ;

 2) ;  Б) ;

 3) ;  В) ;

 4) ;  Г) ;

      Д) .

Відповіді до тесту:

Варіант – І        Варіант – ІІ

1. Б        1. Г

2. А        2. А

3. В        3. А

4. А        4. Б

5. 1. В       5. 1.Д

    2. Д           2. Б

    3. Г           3. В

    4. А           4. А

V. Домашнє завдання.

• Підготувати картку завдань на застосування трьох способів розв’язування ірраціональних рівнянь, та розв’язати їх в зошиті.

Додатково на високий рівень:

• Розв’язати рівняння: .
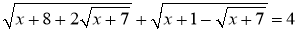• Розв’язати систему рівнянь:

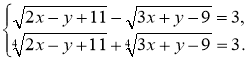
VІ. Підбиття підсумків. Виставлення оцінок.

Голови груп заповнюють листи оцінювання. Оголошуються оцінки.

Рефлексивна бесіда

Студенти обирають ті твердження, які хотіли б продовжити

На занятті я:

• Дізнався/дізналася ....
• Повторив/повторила ....
• Навчився/навчилася ....
• Зробив/зробила успіхи ....
• Труднощі відчував/відчувала у ....
• Мене захопило ....
• Бажаю продовжити …