Розв’язування лінійних нерівностей та систем лінійних нерівностей з однією змінною

Тема: Розв’язування лінійних нерівностей та систем лінійних нерівностей з однією змінною

Мета:

 навчальна: розширити, узагальнити і систематизувати знання про лінійні нерівності і системи лінійних нерівностей; повторити алгоритм розв’язування нерівностей,  закріпити властивості, які використовуються при розв’язуванні нерівностей з однією змінною, а також вдосконалювати знання з розв’язування нерівностей, та  з  графічного зображення множин розв’язків та запису відповідних проміжків, поглибити розуміння в учнів, що в житті людини зустрічається багато нерівностей;

розвивальна: розвивати пам'ять, навички самостійної роботи та

самоаналізу, математичну мову, інтерес до предмета, критичне мислення та впевненість у собі для висловлення власної думки;

 виховна: виховувати наполегливість і відповідальність, допитливість, уважність, натхнення; виховувати свідоме ставлення до навчання та  пізнавальну активність учнів, почуття особистої відповідальності кожного учня  при роботі в колективі, а також ліпити  творчу, всебічно розвинену особистість.

Тип уроку: узагальнення і систематизація знань, умінь та навичок

Обладнання: конспект уроку, підручник, сервіс для відеоконференції Zoom, сканер QR-коду, презентація до уроку, підручник.

Підручник: Істер О.С. Алгебра: підруч. для 9-го кл. загальноовіт.закл./ О.С.Істер. – Київ: Генеза, 2017. – 264с.

Структура уроку:

1. Ознайомлення  з темою, цілями та завданнями уроку.
2. Мотивація учіння.
3. Відтворення здобутих знань.
4. Узагальнення та систематизація знань із встановленням внутрішньо-системних та зовнішньо-системних зв'язків.
5. Підведення підсумків уроку.
6. Повідомлення та пояснення домашнього завдання.

Хід уроку

І. Організаційний етап.

 Добрий день, шановні колеги. Я рада всіх Вас вітати на уроці. Розгорніть Ваші зошити, запишіть сьогоднішню дату та тему.

Дев’ятнадцяте листопада

Класна робота

Розв’язування лінійних нерівностей та систем лінійних нерівностей з однією змінною

Працюючи на уроці, ми будемо поглиблювати  знання, а їх раціональне використання допоможуть успішно написати контрольну роботу.

  На уроці ми використаємо спосіб оцінювання –  самооцінювання, тому сконцентруйтесь і нехай Вам щастить протягом уроку від до . Щоб скачати картку самооцінювання перейдіть за посиланням: https://drive.google.com/file/d/1e2_WiryBszGIAlfNzmq2_6jb6xkH4MKW/view?usp=sharing

Картка самооцінювання

з алгебри

учня (учениці) 9 класу

________________________________

Вид роботи на уроці	Максимальна кількість балів	Кількість балів
Графічний диктант «Так – ні»	2
Тест «Властивості числових нерівностей»	5
Вправа  «Пазли»	2
Задача прикладного характеру	1
Робота з підручником	2
Додаткове завдання	1
Сума балів	12 + 1

 

ІІ. Мотивація учіння

В історії багато прикладів нерівності різних груп людей у своїх правах. Серед таких – бідний – багатий, расова нерівність, гендерна нерівність, нерівність у правах, нерівність у можливостях відносно здорових людей та людей із обмеженими властивостями, фізіологічні відмінності людей (вищий – нижчий, товстий – худий, сильний – слабкий). Ми не можемо змінити світ, зробивши його рівним у можливостях для всіх, але ми можемо бути справедливими та толерантними по відношенню один до одного. Ми повинні з повагою ставитися до людської гідності та прав людини, ми маємо бути відкритими для інших культур, переконань, світогляду.

Наші предки, піднявшись на дві ноги, невтомно передавали  свої знання дітям, для того, щоб вони дійшли до нас. І частину цих знань ми спробуємо відтворити, узагальнити, систематизувати сьогодні на уроці.

Перевіримо теоретичне домашнє завдання за допомогою графічного диктанту «Так – ні». Якщо Ваша відповідь «Так» записуємо цифру «1», якщо ж «Ні», то цифру «0». Кожна правильна відповідь оцінюється у 0,25 бала.

Графічний диктант «Так – ні»

1. Чи є розв’язком нерівності 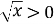будь-яке додатне число?
2. Чи правильно, якщо нерівності  мають різні розв’язки, то їх називають рівносильними?
3. Чи є нерівність 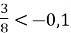– правильною числовою нерівністю?
4. Чи правильно, що при множенні та діленні обох частин нерівності на одне і те саме додатне число, отримаємо нерівність, рівносильну даній?
5. Ч є розв’язком нерівності 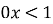проміжок ; .
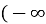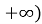6. Чи правильно, що об’єднання числових проміжків – це множина, яка складається з усіх чисел, які належать хоча б одному із цих проміжків?
7. Чи існує ціле число, яке належить проміжку ?
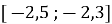8. Чи є нерівність 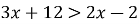строгою?

Ключ до графічного диктанту «Так – ні»

 Виконавши самоперевірку, запишіть кількість балів у картку самооцінювання.

ІІІ. Відтворення здобутих знань

1. Інтерактивна вправа. Тест «Властивості числових нерівностей»

А зараз перевіримо Ваші знання на практиці: проведемо огляд теоретичних вправ на повторення основних властивостей числових нерівностей. Для цього відкриваємо тест за посиланням join.naurok.ua, вводимо код доступу: 6343336  або скануємо додатком для QR-коду (QR-код за посиланням: https://drive.google.com/file/d/1GqkB9yhnthZMmxkmIJ9juqbV6RnXayHj/view?usp=sharing) , який встановлений на Ваш смартфон і вибираємо правильну, на вашу думку, відповідь.

 Кількість балів, отриманих при тестуванні поділіть на 2 та запишіть у картку самооцінювання.

Інтерактивна вправа. Тест «Властивості числових нерівностей»

1. Якщо а – в= 0, то

а) а > в

б) а < в

в) а = в

2. Якщо а – в > 0, то

а) а > в

б) а < в

в) а = в

3. Якщо а – в < 0, то

а) а > в

б) а < в

в) а = в

4. Якщо а > в і с > 0, то

а) ас > вс

б) ас < вс

в) ас = вс

5. Якщо а > в і с < 0, то

а) ас > вс

б) ас < вс

в) ас = вс

6. Якщо а > в, то

а) в > а

б) в < а

в) в = а

7. Якщо а > в і в > с, то

а) а > с

б) а < с

в) а = с

8. Якщо а > в і с будь-яке число, то

а) а + с < в+с

б) а + с > в+с

в) а + с = в+с

9. Якщо а < в і с будь-яке число, то

а) а - с < в - с

б) а - с > в - с

в) а - с = в – с 

10. Якщо а < в і с будь-яке число, то

а) а + с < в+с

б) а + с > в+с

в) а + с = в+с

 

 Ключ до тесту: 1.в;  2.а;  3.б;  4.а;  5.б;  6.б;  7.а;  8.б;  9.а;  10.а.

2. Огляд практичних вправ

Пригадавши властивості числових нерівностей перейдемо до виконання практичних вправ –  виконання інтерактивної вправи «Пазли» з використанням інтернет-сервісу  LerningApps. Перейдіть за посиланням або скористайтеся смартфоном для сканування QR-коду (QR-код за посиланням:  https://drive.google.com/file/d/1NatAdMKZwYacr8S_NB3xfRE_VnXOLlzv/view?usp=sharing

Запишіть у зошиті розв’язання нерівностей. Учень який найшвидше виконав завдання отримує 2 бали. Учні, які частково виконали завдання 1 бал. Учні, які не виконали завдання 0 балів. Для виконання завдання у Вас 5 хвилин.

https://learningapps.org/watch?v=pnxgoov8k20

 

 

Попрацювавши – відпочинемо з користю, погравши у нейропсихологічну гру «Майстерні руки».

IV. Узагальнення та систематизація знань із встановленням внутрішньо-системних та зовнішньо-системних зв'язків

Пригадавши теоретичний матеріал із даної теми, запишемо письмові завдання. Першим нашим номером буде задача прикладного характеру. Один учень за бажанням, включивши демонстрацію свого екрану, виконає задачу письмово на дошці. Правильність виконання даної задачі оцінюється 1 балом.

Прийом «Математична скринька»

Завдання № 1. Задача прикладного змісту

У фермерському господарстві є два яблуневих сади. У першому саду з 90 яблунь зібрали менше 2700 кг яблук. У другому саду з 70 яблунь зібрали більше 1750 кг яблук. Знайти скільки кілограм яблук можливо зібрати з однієї яблуні?

Розв’язання:

Нехай х кг яблук можливо зібрати з однієї яблуні, тоді у першому саду зібрали 90х кг яблук, у другому - 70х кг.  За умовою задачі складаємо і розв’язуємо систему рівнянь:

Отже, з кожної яблуні було зірвано від 25 до 30 кілограм.

Відповідь. .

 Запишемо наступний номер із підручника. Розгортаємо підручник, записуємо № 251(1). Виконуємо завдання самостійно із наступною самоперевіркою. Правильність виконання оцінюється 2 балами.

Завдання № 2. Знайдіть область визначення функції:

№ 251(1)

Розв’язання:

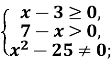
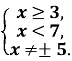
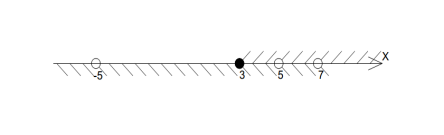
Область визначення функції: .

Завдання № 3. Додаткове завдання.

Пропоную Вам написати незвичну самостійну роботу.

Самостійна робота

1. Замість числа 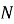впишіть натуральне число із проміжку 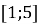та розв’яжіть нерівність.

2. До участі у конкурсі на кращий соціальний плакат «Моє бачення Європи» запрошують молодь. За умовами конкурсу вік учасників 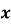становить від 15 до 35 років. Запишіть систему нерівностей для визначення .

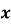Через декілька хвилини учні закінчують розв’язання даної самостійної роботи та перевіряють отриманий результат з екраном. За правильну відповідь учні отримують 1 додатковий бал.

Ключ до самостійної роботи:

1. Відповідь:

Число 1: [1; + ∞);

Число 2: [0,5; + ∞);

Число 3: [; + ∞);

Число 4: [0,4; + ∞);

Число 5: [; + ∞).

2.

V. Підведення підсумків уроку

 Практичне завдання: Намалюйте квітку з п’яти пелюсток і представте її, зазначивши власні потреби як особисті (розмір пелюстки вказує на важливість потреби).

 Підрахуйте кількість балів отриманих протягом уроку та запишіть у картку самооцінювання. Свої результати відправте у приватні повідомлення чи на електронну пошту IRKA2012ukr.net

 На завершення уроку пропоную використати Ваш смартфон для демонстрації самооцінки. Зробіть селфі та покажіть таку емоцію, яка б відображала Ваше почуття на уроці, чи все Ви зрозуміли. Селфі відправте у вайбер-групу та поясніть його одним реченням.

VІ. Повідомлення та пояснення домашнього завдання

Повторити: § 1 – 7.

Письмово:  робота з підручника: Істер О.С. Алгебра: підруч.для 9-го кл. загальноовіт.закл./ О.С.Істер. – Київ: Генеза, 2017. – 264с.

Середній рівень: № 195(1,3), 197;

Достатній рівень: № 207(1,3), 246(1);

Високий рівень: № 250(1), 252.

Додаткове завдання:

Скласти та розв’язати прикладну задачу, яка розв’язується за допомогою лінійної нерівності чи системи лінійної нерівності з однією змінною.

Творче завдання – створити презентацію на тему: «Нерівності навколо нас».   

Завершити наш урок хочу словами Софії Ковалевської: «Серед усіх наук, які відкривають шлях до пізнання законів природи, найвеличнішою є математика». І хочу, щоб Ви пам’ятали, що  не кожна нерівність зі змінною може стати правильною числовою рівністю.

Дякую за урок