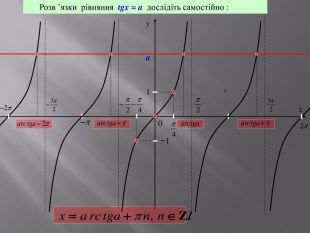
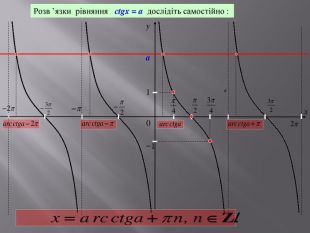
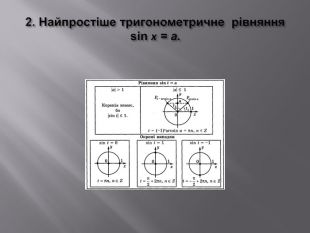
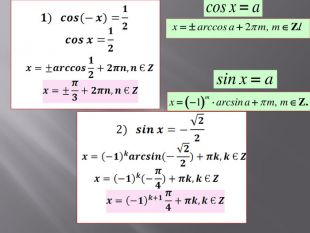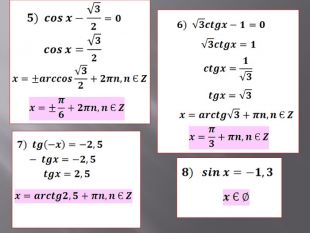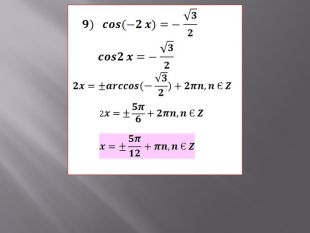Розв’язування найпростіших тригонометричних рівнянь.
Про матеріал
Засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a.,sin t=a, tg t=a, ctg t=a. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



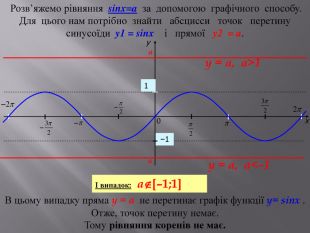
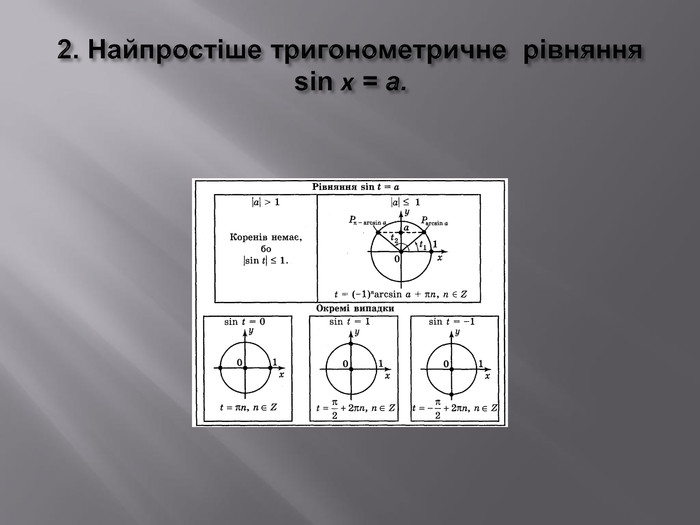
![Розв’яжемо рівняння sinx=a за допомогою графічного способу. Для цього нам потрібно знайти абсцисси точок перетину синусоїди y1 = sinx і прямої y2 = a. В цьому випадку пряма y = a не перетинає графік функції y= sinx . Отже, точок перетину немає. Тому рівняння коренів не має. I випадок: a[–1;1]xy10−1y = a, a>1y = a, a<–1aa Розв’яжемо рівняння sinx=a за допомогою графічного способу. Для цього нам потрібно знайти абсцисси точок перетину синусоїди y1 = sinx і прямої y2 = a. В цьому випадку пряма y = a не перетинає графік функції y= sinx . Отже, точок перетину немає. Тому рівняння коренів не має. I випадок: a[–1;1]xy10−1y = a, a>1y = a, a<–1aa](/uploads/files/27857/159502/172115_images/3.jpg)
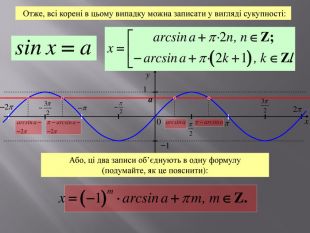
![xy10−1 Очевидно, що в цьому випадку точок перетину безліч, причому їх абсцисси визначаються наступним чином:a1) Розглянемо точку, абсциса якої належить проміжку 2) Абсциса цієї точки – це число(кут), синус якого дорівнює a, тобто значення цього числа дорівнює arcsina. . 3) Абсциса другої точки належить відрізку [–; ] і дорівнює (–arcsina). Щоб це пояснити достатньо пригадати, що sinx = sin(–x).4) Всі інші абсцисси точок перетину отримуємо враховуючи періодичність функції y = sinx (Т=2n, де nZ). Завдання: назвіть абсциси двох наступних точок перетину справа. II випадок: a[–1;1]Відповідь: (arcsina+2π) і (3π – arcsina). xy10−1 Очевидно, що в цьому випадку точок перетину безліч, причому їх абсцисси визначаються наступним чином:a1) Розглянемо точку, абсциса якої належить проміжку 2) Абсциса цієї точки – це число(кут), синус якого дорівнює a, тобто значення цього числа дорівнює arcsina. . 3) Абсциса другої точки належить відрізку [–; ] і дорівнює (–arcsina). Щоб це пояснити достатньо пригадати, що sinx = sin(–x).4) Всі інші абсцисси точок перетину отримуємо враховуючи періодичність функції y = sinx (Т=2n, де nZ). Завдання: назвіть абсциси двох наступних точок перетину справа. II випадок: a[–1;1]Відповідь: (arcsina+2π) і (3π – arcsina).](/uploads/files/27857/159502/172115_images/4.jpg)
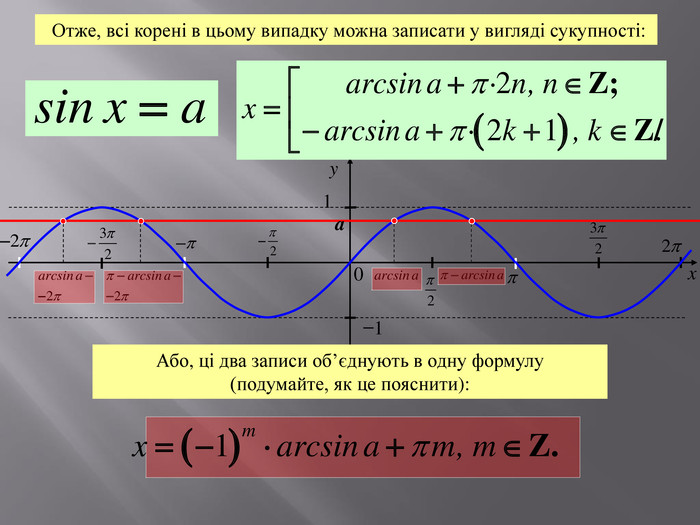
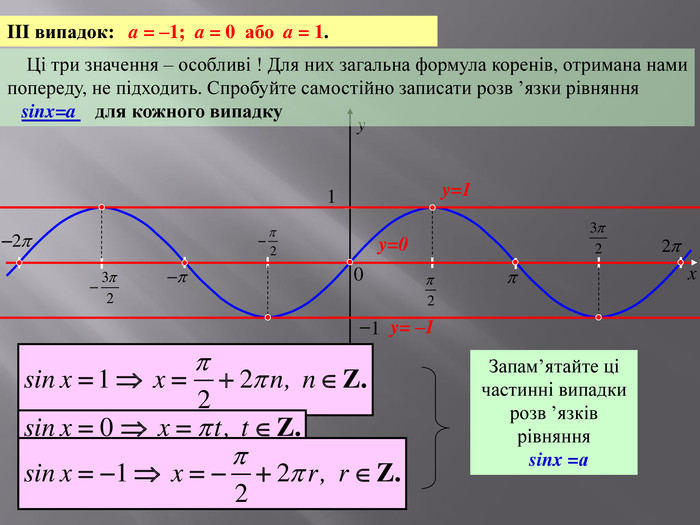
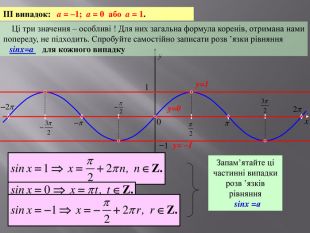
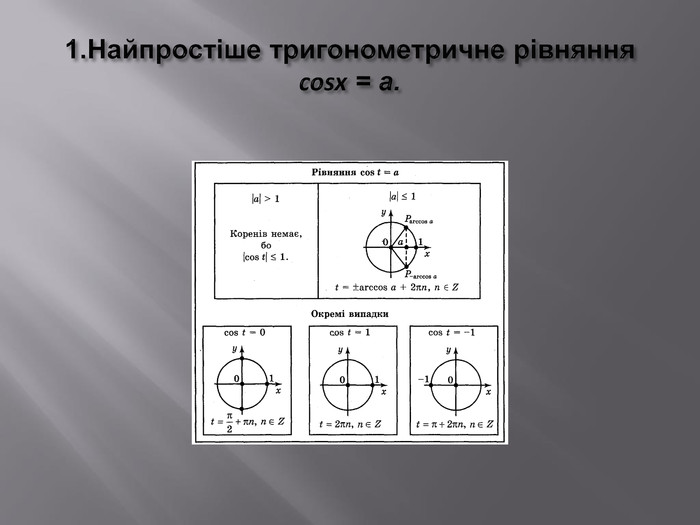
![xy10−1 Розв’яжемо рівняння cosx=a теж за допомогою графічного способу. Для цього нам потрібно знайти абсцисси точок перетину косинусоїди y = cosx та прямої y = a. I випадок: a[–1;1]Очевидно, що в цьому випадку точок перетину немає. Тому рівняння коренів не має.y=a, a>1y=a, a< –1aa xy10−1 Розв’яжемо рівняння cosx=a теж за допомогою графічного способу. Для цього нам потрібно знайти абсцисси точок перетину косинусоїди y = cosx та прямої y = a. I випадок: a[–1;1]Очевидно, що в цьому випадку точок перетину немає. Тому рівняння коренів не має.y=a, a>1y=a, a< –1aa](/uploads/files/27857/159502/172115_images/7.jpg)
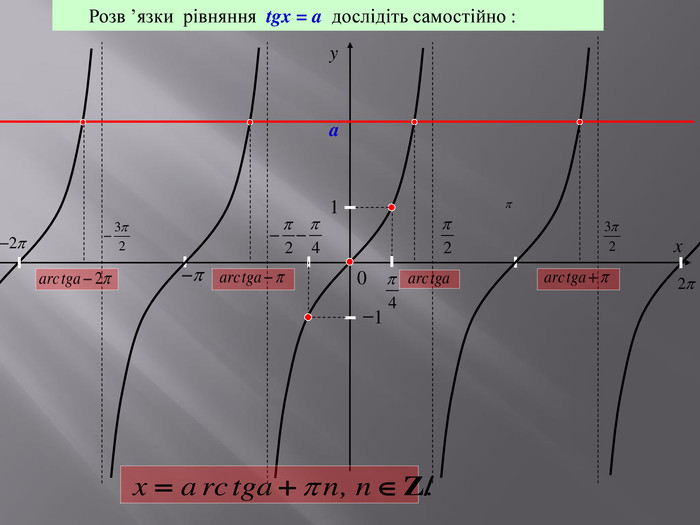
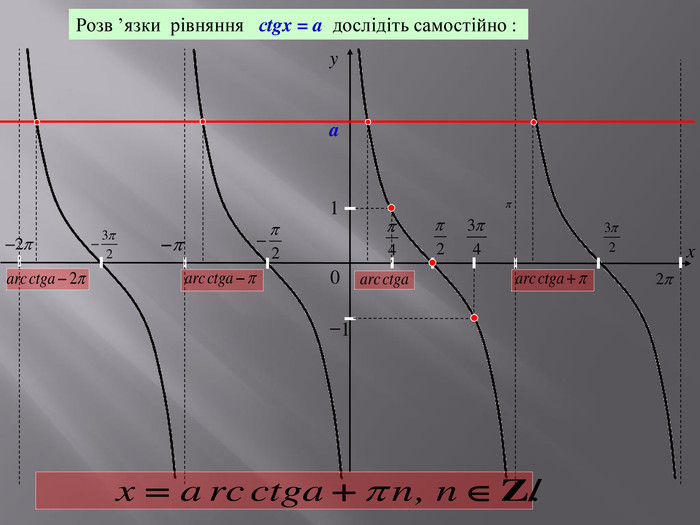
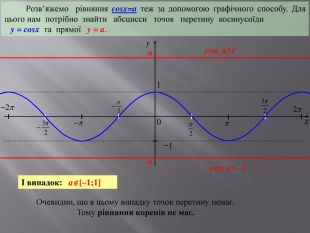
![Розв’язання будь-яких тригонометричних рівнянь зводиться до розв’язання найпростіших тригонометричних рівнянь, які ми розглянули вище. Для цього застосовуються відомі Вам тотожні перетворення, різні тригонометричні формули, різні способи розв’язування алгебраїчних рівнянь, формули скороченого множення и т.п. Отже, запам’ятайте : a[–1;1] Розв’язання будь-яких тригонометричних рівнянь зводиться до розв’язання найпростіших тригонометричних рівнянь, які ми розглянули вище. Для цього застосовуються відомі Вам тотожні перетворення, різні тригонометричні формули, різні способи розв’язування алгебраїчних рівнянь, формули скороченого множення и т.п. Отже, запам’ятайте : a[–1;1]](/uploads/files/27857/159502/172115_images/10.jpg)

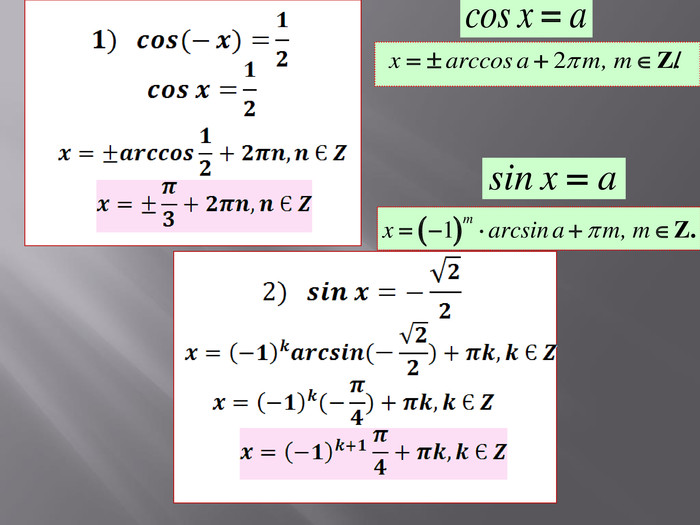

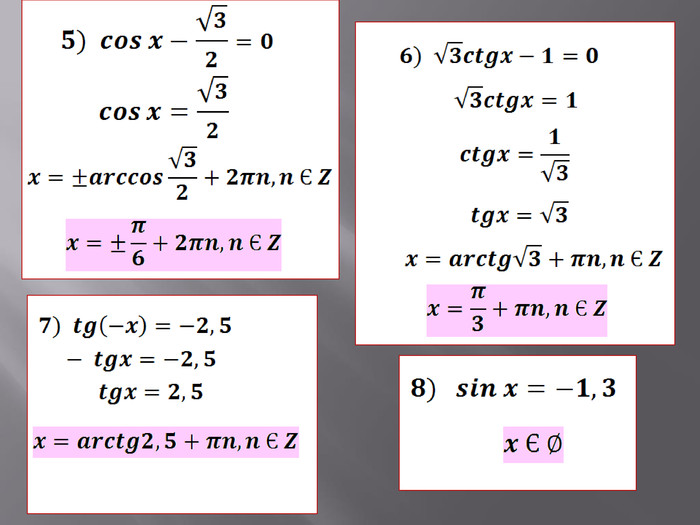










![7. Що таке арккосинус числа а? Чому дорівнює арккосинус від’ємного аргументу? Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а. arccos (-а) = π - arccos а. 7. Що таке арккосинус числа а? Чому дорівнює арккосинус від’ємного аргументу? Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а. arccos (-а) = π - arccos а.](/uploads/files/27857/159502/172115_images/27.jpg)