Розв'язування нерівностей з однією змінною.

Про матеріал

повторити матеріал «квадратична функція», формувати вміння та навички розв'язувати нерівності з однією змінною, удосконалювати навички самостійної діяльності учнів

Перегляд файлу

«Від того настрою, з яким ви вступаєте в день,

або в якусь справу, залежать ваші успіхи…»

Конфуцій

Розв'язування нерівностей з однією змінною.

Мета: повторити матеріал «квадратична функція», формувати вміння та навички розв’язувати нерівності з однією змінною, удосконалювати навички самостійної діяльності учнів; розвивати пізнавальні здібності, уважність; формувати в учнів науковий погляд на матеріальний світ; виховувати інтерес до навчання та культуру виконання рисунка.

Обладнання: картки для роботи в групах.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

І Організаційний етап

Доброго дня, світлої днини

Так привітаю кожну дитину Здрастуйте, скажу колегам усім

Друзям, гостям і знайомим моїм.

В 9 класі ми з вами трудились

Графіки розрізняти добре навчились

Квадратні нерівності вже підкорили

Як знайти діагональ,

Що сховалась за вуаль.

Інтервал вже не страшний,

Вмить впізнаєм, хто такий

Що навчилися покажем

I з півслова все розв'яжем.

Один одному всміхнімся,

Група групі поклонімся,

Зберем в'язочку думок

I почнемо наш урок.

Досягнення успішного результату під час розв'язування задач - зовсім не привілей математики. Усе людське життя — це не що інше, як бажання досягти успіху в розв'язуванні все нових питань і проблем. Як досягти успіху? Це питання справді постає перед нами практично кожного дня. Будьте уважними протягом уроку і кожен із вас в кінці висловить свої враження

ІІ Формулювання мети і завдань уроку

Девізом сьогоднішнього уроку нехай будуть слова

Коли починаєш справу, спитай себе: «Що я маю зробити?»

Після закінчення: «Що я зробив?»

Піфагор

Досягти певних результатів розв'язування можна лише тоді, якщо є мета, тому ми сформулюємо очікувані результати, які будемо прагнути досягти протягом уроку.

Очікуванні результати

• Удосконалити навички
- побудови графіків квадратичних функцій;

- розв'язування квадратних нерівностей графічним методом, методом інтервалів;

- розв'язування дробово-раціональних нерівностей;

• Узагальнити і систематизувати знання про квадратичні функції, їх властивості.

ІІІ Перевірка домашнього завдання

А зараз ми перевіримо домашнє завдання

ІV Актуалізація опорних знань та вмінь

Зараз ми проведемо інтерактивне опитування «Вільний мікрофон».

Дати означення функції.
Дати означення квадратичної функції.

Формули для обчислення абсциси вершини параболи.
Як визначити, куди напрямлені вітки параболи?
Що називається нулями функції?
Що називається квадратним тричленом?
Яка формула розкладання квадратного тричлена на лінійні множники?
Дати означення квадратної нерівності з однією змінною.
Сформулювати алгоритм розв'язування квадратних нерівностей способом інтервалів.

Записуємо в зошити число, класна робота

Математичний диктант з взаємоперевіркою.

Варіант 1.

Знайдіть область визначення функції
Знайдіть проміжки спадання функції
Знайдіть значення аргументу при яких функція набуває від’ємних значень.
Знайдіть найменше значення функції

Варіант 2.

Знайдіть множину значень функції
Знайдіть проміжки зростання функції
Знайдіть значення аргументу при яких функція набуває додатніх значень.
Знайдіть найбільше значення функції

Записати графіки функцій, які зображені на слайді

синій

червоний

2. Підготовка до ДПА

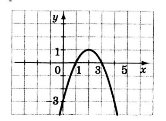
1) На рисунку зображено графік функції у=-х²+4х-3. Розв’яжіть нерівність –х²+4х-3 ≤0.

$\\TEACHER-PC\Users\Public\Скани\img042.jpg$

А) [-1; 3];

Б) (-∞; 1)(3;+∞)

В) (-∞; 1][3;+∞);

Г) [0;1].

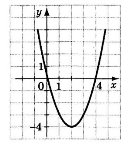
2) На рисунку зображено графік функції у=х²- 4х. Укажіть найбільше ціле число, яке є розв’язком нерівності х²- 4х< 0.

$\\TEACHER-PC\Users\Public\Скани\img043.jpg$

А) 4;

Б) -4;

В) 3;

Г) такого числа не існує.

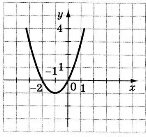$\\TEACHER-PC\Users\Public\Скани\img044.jpg$ 3) На рисунку зображено графік функції у=х² + 2х. Знайдіть множину розв’язків нерівності х² + 2х ≤ 0.

А) (-2;0);

Б) [-2;0];

В)[-1;0];

Г) (-∞;-2] [0;+∞).

4) Розв’яжіть нерівність х²- 4х-12>0 (графічний метод І варіант)

-х²-2х+3>0 (графічний метод ІІ варіант)

V. Узагальнення та систематизація знань учнів.

1) Робота в групах.

Картка 1

Розв’язати нерівність x(x-5)(x+6) > 0

(-6;0) (5;+∞)	(0;5)	(-∞;-6)
дізнатись	зробити	виконати

(Відповідь: дізнатись)

Картка2

Розв’язати нерівність (x+9)(x-2)(x-15) < 0

(-9;2)	(-∞;-9)	(-9;2)∞)
математика	як приємно	гарно

(Відповідь: як приємно)

Картка 3

Знайти область визначення функції

[-8;5]	(-	(-8;5)
чогось	когось	навіщо

(Відповідь: чогось)

Картка 4

Розв’язати нерівність (х²-16)(х+17) > 0

(-17; -4)	(-4;4)	(-17; -4)
Мольєр	Піфагор	Паскаль

(Відповідь: Мольєр)

Картка 5

Розв’язати нерівність < 0

(5; +∞)	( -∞; -6)	(-6;5)
що вони	що ми	що ти

(Відповідь: що ти)

Картка 6

Знайти область визначення функції

(1;9)		[-12;1]
виконав	показав	навчився

(Відповідь: навчився)

А зараз прочитайте свої відповіді згідно номерів карточок, які ви виконували.

Складіть правильний вираз.

Правильний вислів: «Як приємно дізнатись, що ти чогось навчився» Мольєр

Майбутній драматург жив у будинку, який парижани називали «мавпячим». На рогах приємної триповерхової споруди будівельник XV століття розташував скульптурні дерев’яні зображення помаранчевих дерев, на яких маленькі мавпочки зривали плоди. «Доброзичливці» казали, що нічого дивного немає в тому, що старший син шановного Поклена став блазнем.

Драматург не відмовився від своїх мавп і на схилі віку, проектуючи свій герб, зобразив на ньому своїх хвостатих приятельок, які стерегли батьківський будинок.

Коли зібралися ховати Мольєра, під його вікнами зібралася велика кількість людей, щоб завадити цьому. В результаті його поховали в тому відділі, де ховають нехрещених і самовбивць.

VI. Підведення підсумку

Учитель. Повернемось до початку уроку, до мети, яку ми ставили перед собою. Поміркуємо, чи досягли ми її? Чи удосконалили навички побудови графіків квадратичних функщй; розв'язування квадратних нерівностей графічним методом, методом інтервалів; розв'язування дробово-раціональних нерівностей;