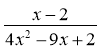Розв’язування рівнянь, що зводяться до квадратних рівнянь

Середній рівень

(кожне завдання по 2 б.)

Достатній рівень

(кожне завдання по 3 б.)

Високий рівень

(кожне завдання по 4 б.)

1.Розв’язати рівняння

1) ;

2) х⁴ – 6x + 5 = 0.

1.Розв’язати рівняння

1) .

2) (х² + 5х + 1)(х² + 5х + 3) + +1 = 0

1.Розв’язати рівняння

1) .

2)(2х+1)⁴ –29  (2х+1)² +100= 0.

2.Розкласти на множники квадратний тричлен:

1. x² – 9x + 14;
2. 5x² + 11x + 2.

2.Скоротити дріб

.

2.Скоротити дріб

.

3. Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.

3.За два дні спільної роботи два робітники виконали третину завдання. За скільки днів може виконати це завдання кожний робітник, працюючи окремо, якщо перший робітник може виконати його на 5 днів швидше, ніж другий?

3. З пункту А в пункт В, відстань між якими дорівнює 120 км, виїхав автобус, а через 14 хв слідом за ним виїхав легковий автомобіль, швидкість якого на 20 км/год більша від швидкості автобуса. Знайти швидкість автобуса, якщо у пункт В він приїхав на 16 хв пізніше від автомобіля.

Середній рівень

(кожне завдання по 2 б.)

Достатній рівень

(кожне завдання по 3 б.)

Високий рівень

(кожне завдання по 4 б.)

1.Розв’язати рівняння

1).

2)х⁴ – 8х² + 7 = 0

1.Розв’язати рівняння

1) .

2)(х² – 5х + 4)(х² – 5х + 1) = 28

1.Розв’язати рівняння

1)  

2)(х + 3)⁴ – 20  (х + 3)² + 64 = 0.

2.Розкласти на множники квадратний тричлен:

1. x² – 11x + 24;
2. 7x² + 6x – 1.

2.Скоротити дріб

.

2.Скоротити дріб .

3.Моторний човен пройшов 3 км за течією річки і 1 км проти течії, витративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 1 км/год.

3.За 40 годин спільної роботи дві бригади робітників виконали завдання. За скільки днів може виконати завдання кожна з бригад, якщо перша з них може це зробити на 22 години раніше, ніж друга?

3.З пункту А в пункт В, відстань між якими дорівнює 30 км, виїхав мотоцикліст, а через 6 хв слідом за ним виїхав автобус, швидкість якого на 10 км/год більша від швидкості мотоцикліста. Знайти швидкість автобуса, якщо у пункт В він приїхав на 4 хв раніше від мотоцикліста.

Середній рівень

(кожне завдання по 2 б.)

Достатній рівень

(кожне завдання по 3 б.)

Високий рівень

(кожне завдання по 4 б.)

1.Розв’язати рівняння

1) .

2)9х⁴ – 37х² + 4 = 0

 1.Розв’язати рівняння

1) .

2)(х² – 2x)² – 3(х² – 2х) – 4 = 0

1.Розв’язати рівняння

1) .

2)(х² + х)² – 8  (х² + х) + 12 = 0.

2.Розкласти на множники квадратний тричлен:

1) x² – 4x + 3;

2) 4x² – 9x + 2.

2.Скоротити дріб .

2.Скоротити дріб .

3.З пункту А до пункту В, відстань між якими дорівнює 40 км, виїхали одночасно два велосипедисти. Швидкість одного з велосипедистів на 2 км/год менша від швидкості другого, тому він прибув до В на 1 год пізніше. Знайти швидкість кожного з велосипедистів.

3.Перша бригада повинна була виготовити 60 деталей, а друга — 72 деталі. Перша бригада виготовляла щогодини на 4 деталі більше, ніж друга, і працювала на 1,5 год менше від другої. Скільки деталей виготовляла кожна бригада за 1 год?

3. З пункту А в пункт В, відстань між якими 4 км, відправились два пішоходи. Другий пішохід вийшов на 10 хв пізніше першого, але прийшов у пункт В на 2 хв раніше. Знайти швидкість другого пішохода, якщо вона на 1 км/год більша від швидкості першого пішохода.