Розв’язування систем рівнянь
ЗМІСТ
I. Системи рівнянь та основні їх властивості.
II. Розв’язування систем лінійних рівнянь.
1) Спосіб підстановки.
2) Спосіб додавання.
3) Спосіб порівняння.
4) Формули Крамера.
5) Метод Гаусса.
III. Розв’язування систем нелінійних рівнянь.
1) Застосування теореми Вієта.
2) Спеціальний прийом.
3) Розв’язування систем ірраціональних рівнянь.
4) Розв’язування логарифмічних рівнянь.
5) Показникові системи та їх розв’язування.
6) Комбіновані системи.
7) Системи тригонометричних рівнянь.
IV. Кругові та симетричні системи.
V. Висновок
Системи рівнянь та їх основні властивості.
Системою рівнянь називається будь - яка скінченна множина рівнянь. Системи рівнянь виникають при розв’язуванні задач математики, фізики та інших наук, де невідомою є не одна величина , а декілька. Ці величини зв’язані певними залежностями, які записуються у вигляді рівнянь.
Якщо система має хоча б один розв’язок , то вона називається
сумісною. Якщо ж розв’язків система не має , то вона називається несумісною.
Слово “несумісність” наочно показує , що різні рівняння системи накладують несумісні одна з одною умови, які повинні задовольняти невідомі.
У загальному випалку можна розглядати системи m рівнянь з n невідомими, при чому можливі всі три випадки: m=n , m< n і m>n. Розв’язком системи рівнянь з n невідомими називається впорядкований набір з n чисел, який є розв’язком кожного з рівнянь системи.
Розв’язати систему - означає знайти всі її розв’язки.
Дві системи рівнянь називаються рівносильними, якщо вони мають одну й ту ж множину розв’язків.(Дві несумісні системи за означенням вважаються рівносильними.)
Сформулюємо деякі правила перетворення систем:
1) Якщо в системі замінити яке - небудь з рівнянь на йому рівносильне, а решту залишити без зміни, то одержана система рівносильна даній.
2) Нехай f=g і - які - небудь два рівняння систем. Тоді якщо в системі замінити рівняння f=g на рівняння f++g (називається сумою рівнянь f=g і ), а решту залишити без зміни, то одержана система рівносильна даній.
3) Нехай система містить рівняння x= , де x- деяка змінна, а - деяка функція незалежна від x. Тоді якщо у всіх рівняннях системи, крім рівняння x= , замість x підставити , одержана система рівносильна даній.
4) Якщо система містить рівняння fg=0, то вона розкладається на дві системи, в одній із них рівняння fg=0 замінено на f=0, а в другій - на g=0. При цьому кожний розв’язок даної системи є розв’язком однієї з одержаних систем.
Якщо ж функції f і g визначені на одній і тій же множині, то кожний розв’язок одержаних систем є розв’язком даної системи.
В цьому випадку говорять, що дана система рівносильна сукупності одержаних систем.
В шкільному курсі вивчення математики розглядаються в основному системи лінійних рівнянь та системи рівнянь вищого ступеня. Так як при розв’язувані всих видів систем рівнянь рівняння в системах зводяться до лінійних та найпростіших рівнянь вищого ступеня, то основну увагу я звернув на розв’язування систем лінійних рівнянь та систем найпростіших рівнянь вищого ступеня.
Також особливу увагу я звернув на розв’язування систем рівнянь
методом Гаусса та формулами Крамера, які не розглядаються в шкільному курсі.
СИСТЕМИ РІВНЯНЬ
Сукупність декількох рівнянь з декількома невідомими називають системою рівнянь (невідоме, позначене одною і тією ж літерою в кожному із рівнянь, повинно позначати одну й ту ж невідому величину).
Наприклад:![]()
 система двох рівнянь з двома невідомими;
система двох рівнянь з двома невідомими;
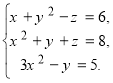 система трьох рівнянь з трьома невідомими;
система трьох рівнянь з трьома невідомими;
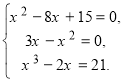 система трьох рівнянь з одним невідомим.
система трьох рівнянь з одним невідомим.
Розв’язком системи рівнянь з декількома невідомими називається сукупність значень цих невідомих , перетворююча кожне рівняння системи в тотожність.
Наприклад, система
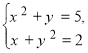
має розв’язок x=2, y=1, так як при цих значеннях невідомих рівняння системи перетворюються в тотожності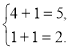
Розв’язати систему рівнянь, означає знайти множину всіх її розв’язків або показати, що вона розв’язків не має.
Якщо система не має розв’язків то її називають несумісною.
Приклад.Розв’язати систему ( x )
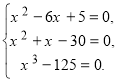
![]()
Розв’язуючи окремо кожне рівняння системи, маємо :
1) x=1 або x=5,
2) x=6 або x=5,
3) x=5.
Відповідь: x=5.
Дві системи рівнянь з одними й тими ж невідомими називаються рівносильними або еквівалентними, якщо кожний розв’язок першої системи являється розв’язком другої і, навпаки, кожний розв’язок другої системи являється розв’язком першої або якщо обидві системи розв’язків не мають.
Приклад. Довести, що системи рівнянь
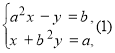 і
і 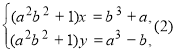
рівносильні в множині дійсних чисел (a0,b0). Нехай пара чисел будь-який розв’язок системи (1), тобто
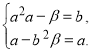
Помножемо обидві частини першої тотожності на b![]() і додамо отриману тотожність до другої, а тоді обидві частини другої тотожності помножимо на a
і додамо отриману тотожність до другої, а тоді обидві частини другої тотожності помножимо на a![]() і віднімемо з отриманої першої тотожності.
і віднімемо з отриманої першої тотожності.
В результаті отримаємо тотожності 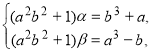
які означають, що пара чисел розв’язки системи (2). Нехай пара чисел будь- який розв’язок системи (2), тобто
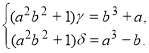
![]()
Помноживши обидві частини першої тотожності на 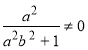 , а другого на
, а другого на ![]() і додавши їх, отримаємо тотожність
і додавши їх, отримаємо тотожність
 або
або 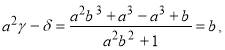
тобто ![]() .
.
Помноживши обидві частини першої тотожності на ![]() , а другого на
, а другого на 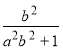 і додавши отримані тотожності, отримаємо
і додавши отримані тотожності, отримаємо ![]() .
.
Таким чином 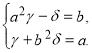
Отриманий результат означає, що пара чисел розв’язок системи(1).
Звідси, системи (1) і (2) рівносильні при a0 і b0.Можна показати,що якщо хоча б один із параметрів a і b або обидва рівні нулю, отже системи (1) і (2) також рівносильні.
|
Системи лінійних рівнянь |
|
з двома і трьома невідомими |
Система 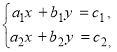 (1), де x і y невідомі, а
(1), де x і y невідомі, а ![]() коефіцієнти системи, називаються системою двох лінійних рівнянь з двома невідомими.
коефіцієнти системи, називаються системою двох лінійних рівнянь з двома невідомими.
Якщо ![]() , то система називається однорідною, в інших випадках неоднорідною.
, то система називається однорідною, в інших випадках неоднорідною.
Основні способи розв’зування системи двох лінійних рівнянь з двома невідомими:
1. Спосіб підстановки.
Щоб розв’зати систему (1) , з першого рівняння системи знайдемо при ![]()
![]() підставивши знайдене значення y у друге рівняння системи (1) отримаємо:
підставивши знайдене значення y у друге рівняння системи (1) отримаємо: ![]()
звідки ![]()
то ![]()
Тоді ![]()
Таким чином, розв’язком системи (1) при ![]() являється пара чисел
являється пара чисел
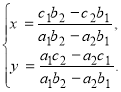 (2)
(2)
2. Спосіб алгебраїчного додавання.
Щоб розв’язати систему
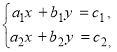 (1)
(1)
способом алгебраїчного додавання, помножимо обидві частини першого рівняння на ![]() і другого на
і другого на ![]() . Отримуємо:
. Отримуємо:
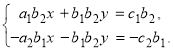
![]() Вважаючи, що система має розв’язки, додаємо ліву і праву частини рівняння системи; отримаємо
Вважаючи, що система має розв’язки, додаємо ліву і праву частини рівняння системи; отримаємо
![]()
звідки знаходимо при ![]()
![]()
Аналогічно знаходимо y. Помноживши обидві частини першого рівняння системи (1) на ![]() а другого на
а другого на ![]() отримуємо
отримуємо
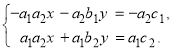
Додаємо ліві і праві частини рівнянь: ![]()
звідки при ![]()
![]()
Таким чином, 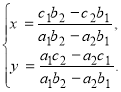 якщо
якщо ![]() .
.
3.Спосіб порівняння.
Щоб розв’язати систему (1)
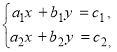
способом порівняння, знайдемо y або x з кожного рівняння системи:
![]()
знайдемо: 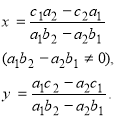
Таким чином, система 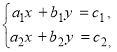 якщо
якщо ![]() має розв’язки
має розв’язки
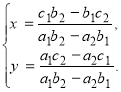
4.Формули Крамера.
Головний і допоміжний визначники системи
двох лінійних рівнянь з двома невідомими.
Головним визначником системи рівнянь ![]()
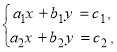 називається визначник
називається визначник
![]()
![]()
складання із коефіцієнтів при невідомих х іу . Цей визначник ми будемо позначати грецькою буквою (дельта). Очевидно , що = a1 b2 - a2 b1![]()
![]()
![]()
Першим допоміжним визначником системи рівнянь ( 1 ) називається визначник
![]() .
.
Він виходить із головного визначника цієї системи рівнянь шляхом заміни першого стовпчика на стовпчик вільних членів. Цей визначник ми будемо позначати х . Показник ( тобто х ) при вказує, що в головному визначнику
перший стопчик ![]() , складений з коефіціентів при х в системі рівнянь (1), замінений на стопчик вільних членів
, складений з коефіціентів при х в системі рівнянь (1), замінений на стопчик вільних членів ![]() . Очевидно , що х =c1b2
. Очевидно , що х =c1b2 ![]() .
.
Другим допоміжним визначником системи рівнянь (1) називається визначник
![]() ,який отримується з головного визначника цієї системи шляхом заміни другого стопчика на стопчик вільних членів .
,який отримується з головного визначника цієї системи шляхом заміни другого стопчика на стопчик вільних членів .
Цей визначник ми будемо позначати у. Очевидно , що у =c1b2 ![]() .
.
Для системи рівнянь
![]()
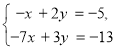
=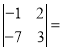 (1
(1
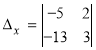 =1;
=1;
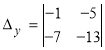
Питання в тому, яку користь приносить введенні нами визначники ![]() при рішенні системи рівнянь (1), ми з’ясуємо пізніше.
при рішенні системи рівнянь (1), ми з’ясуємо пізніше.
Теорема (*). Якщо головний визначник системи рівнянь 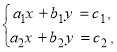 (1) не дорівнює нолю,то ця система рівнянь сумісна і має єдиний розв’язок:
(1) не дорівнює нолю,то ця система рівнянь сумісна і має єдиний розв’язок: ![]() (*)
(*)
Наприклад, для системи 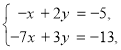 розглянутої вище ,
розглянутої вище , ![]() . Оскільки то система сумісна і має єдиний розв’язок:
. Оскільки то система сумісна і має єдиний розв’язок:![]()
Доведення теореми (*)
1) Спочатку покажемо, що при ![]() система (1) не може мати більше одного розв’язку.
система (1) не може мати більше одного розв’язку.
Нехай ![]() розв’язки системи (1). Тоді
розв’язки системи (1). Тоді 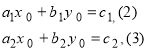
Помножемо перше з цих рівнянь на b![]() , а друге на -
, а друге на -![]() і отримані відношення додамо. Отже маємо:
і отримані відношення додамо. Отже маємо:
(![]() або
або ![]()
Тоді до рівняння (2), помноженого на -![]() , додамо рівняння (3), помножене на
, додамо рівняння (3), помножене на ![]()
Звідси дістанемо:
(![]()
або ![]() .
.
Таким чином, якщо система рівнянь (1) має розв’язки ![]() ,то
,то
![]()
![]() .
.
Внаслідок того, що![]() повинен бути рівний
повинен бути рівний ![]() , а
, а ![]() =
=![]()
Ніякими іншими числами ![]() бути не можуть. Але це і означає, що дана система має не більше одного розв’язку.
бути не можуть. Але це і означає, що дана система має не більше одного розв’язку.
2) Доводячи єдинність розв’язку системи рівнянь (1), ми припускали, що рівняння існує. Але чи правильне таке припущення? Тепер це питання з’ясувати не важко.
Ми вже показали, що розв’язком системи рівнянь (1) можуть бути лише числа ![]() і
і ![]() =
=![]() Тому тепер нам потрібно буде просто підставити ці значення x і y в рівняння системи (1) і подивитися, чи перетворюються ці рівняння в числові рівності. Якщо перетворються, то тим самим ми доведемо, що система рівнянь (1) має розв’язки
Тому тепер нам потрібно буде просто підставити ці значення x і y в рівняння системи (1) і подивитися, чи перетворюються ці рівняння в числові рівності. Якщо перетворються, то тим самим ми доведемо, що система рівнянь (1) має розв’язки ![]() ,
, ![]() =
=![]() і, отже є сумісною. В цьому і полягає другий етап доведення теореми (*). Маємо:
і, отже є сумісною. В цьому і полягає другий етап доведення теореми (*). Маємо: 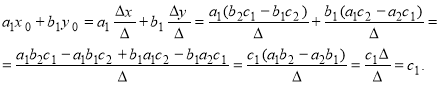
Аналогічно доводимо, що ![]() Таким чином, якщо для системи рівнянь (1) , то ця система має розв’язок і при тому лише один. Його можна отримати за слідуючим правилом: знаходимо
Таким чином, якщо для системи рівнянь (1) , то ця система має розв’язок і при тому лише один. Його можна отримати за слідуючим правилом: знаходимо
![]() а потім обчислюємо шукані величини x і y за формулами
а потім обчислюємо шукані величини x і y за формулами ![]() Це правило названо ім’ям швейцарського математика Крамера (1704 1752), який одним з перших прийшов до поняття визначника і довів наведену вище теорему.
Це правило названо ім’ям швейцарського математика Крамера (1704 1752), який одним з перших прийшов до поняття визначника і довів наведену вище теорему.
Умова ![]()
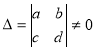
![]() озгначає, що ряди (a,b) і (c,d) цього визначника не пропорційні. В такому випадку говорять, що коефіцієнти при невідомих x і y в системі рівнянь (1) не пропорційні. Тому отриманий результат можна сформулювати слідуючим чином.
озгначає, що ряди (a,b) і (c,d) цього визначника не пропорційні. В такому випадку говорять, що коефіцієнти при невідомих x і y в системі рівнянь (1) не пропорційні. Тому отриманий результат можна сформулювати слідуючим чином.
Якщо коефіцієнти при невідомих x і y в системі рівнянь 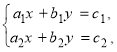 не пропорційні, то ця система сумісна і має єдиний розв’язок.
не пропорційні, то ця система сумісна і має єдиний розв’язок.
Питання про пропорційність коефіцієнтів при невідомих часто розв’язуються усно.Тому усно може бути встановлена сумісність таких, наприклад, систем, як 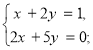
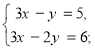
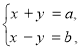 і т. д.
і т. д.
Разом з тим усно виясняється, що кожна з даних систем має лише один розв’язок.
Випадок, коли головний визначник системи рівнянь
дорівнює нулю, а хоча б один з допоміжних визначників
відмінний від нуля
Теорема. Якщо головний визначник системи рівнянь 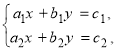 (1) рівний нулю, а хоча б один з допоміжних визначників відмінний від нуля, то система несумісна.
(1) рівний нулю, а хоча б один з допоміжних визначників відмінний від нуля, то система несумісна.
Формально доведення цієї теореми не важко отримати методом від супротивного. Припустимо, що система рівнянь (1) має розв’язок ![]() . Тоді, як показано вище,
. Тоді, як показано вище, ![]() (2). Але за умовою =0, а хоча б один із визначників
(2). Але за умовою =0, а хоча б один із визначників ![]() і
і ![]() відмінний від нуля. Таким чином, рівності (2) одночасно виконуватися не можуть. Теорема доведена.
відмінний від нуля. Таким чином, рівності (2) одночасно виконуватися не можуть. Теорема доведена.
Але представляється цікавішим більше з’ясувати, чому система рівнянь (1) в розглянутому випадку несумісна ?
Зміст =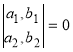
означає, що коефіцієнти при невідомих в системі рівнянь (1) пропорційні.
Нехай, наприклад,
![]()
![]()
Зміст 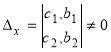
означає, що коефіцієнти при y і вільні члени рівнянь системи (1) не пропорційні
Оскільки ![]() то
то ![]()
Отже, система рівнянь (1) може буть записана в слідуючому вигляді:
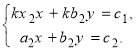
В цій системі коефіцієнти при невідомих відносно пропорційні, але коефіцієнти при y (або при x) і вільні члени не пропорційні. Така система, зрозуміло, несумісна.
Дійсно, якщо б вона мала розв’язок ![]()
![]() то виконувались би числові рівності
то виконувались би числові рівності
![]()
![]()
![]()
Але одна з цих рівностей протирічить другій : так як ![]()
Ми розглянули тільки випадок, коли ![]() Аналогічно може бути розглянутий випадок, коли
Аналогічно може бути розглянутий випадок, коли ![]()
Доведену теорему можна сформулювати і таким чином.
Якщо коефіцієнти при невідомих x i y в системі нерівностей (1) пропорційні, а коефіцієнти при якому-небуть з цих невідомих і вільні члени не пропорційні, то ця система нерівностей несумісна.
Легко, наприклад, переконатися в тому, що кожна із даних систем буде несумісною:![]()
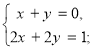
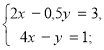
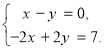
Випадок, коли і головний і обидва допоміжних визначника
системи рівнянь дорівнюють нулю
Ми розглянули вище, вивчаючи систему рівнянь 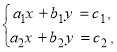 (1)
(1)
обидва випадки:
1) випадок, коли коефіцієнти при невідомих х і у не являються відповідно пропорційними 0
2) випадок, коли коефіцієнти при невідомих х і у відповідно пропорційні, а коефіцієнти при якому-небудь невідомому і вільні члени не являються відповідно пропорційними 0, а хоча б один із визначників ![]() і
і![]() відмінний від нуля.
відмінний від нуля.
Залишилося розглянути ще один випадок, коли і коефіцієнти при невідомих х і у та вільні члени відповідно пропорційні, тобто
![]()
або
![]()
Для визначеності ми розглянемо перший із цих двох варіантів. Система рівнянь (1) в такому випадку має вид :
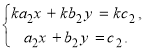 (2)
(2)
Очевидно, що кожна пара чисел ![]() задовольняючи друге рівняння системи (2), повинна задовольняти і перше рівняння цієї системи. Тому, для того щоб розв’язати систему рівнянь (2), достатньо розв’язати лише друге рівняння цієї системи. Іншими словами, достатньо знайти всі такі пари чисел
задовольняючи друге рівняння системи (2), повинна задовольняти і перше рівняння цієї системи. Тому, для того щоб розв’язати систему рівнянь (2), достатньо розв’язати лише друге рівняння цієї системи. Іншими словами, достатньо знайти всі такі пари чисел![]() які перетворюють рівняння
які перетворюють рівняння ![]() у числову рівність.
у числову рівність.
Припустимо, що в цьому рівнянні хоча б один із коефіцієнтів ![]() і
і ![]() відмінний від нуля. Нехай, наприклад,
відмінний від нуля. Нехай, наприклад, ![]() Тоді в якості
Тоді в якості ![]() можна вибрати будь-яке число t;
можна вибрати будь-яке число t; ![]() в цьому випадку знаходиться із умови
в цьому випадку знаходиться із умови ![]() звідки
звідки
![]() де t будь-яке число.
де t будь-яке число.
Цей результат ми отримали в припущенні, що хоча б один із коефіцієнтів ![]() і
і ![]() відмінний від нуля. А якщо вони обидва дорівнюють нулю? Тоді система рівнянь (2) має вид :
відмінний від нуля. А якщо вони обидва дорівнюють нулю? Тоді система рівнянь (2) має вид :
![]()
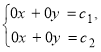 (3)
(3)
Така система не являється особо цікавою. Якщо ![]() то розв’язком її являється будь-яка пара чисел
то розв’язком її являється будь-яка пара чисел ![]() . Якщо ж хоча б одне з чисел
. Якщо ж хоча б одне з чисел ![]() і
і ![]() відмінні від нуля, то система (3) не сумісна.
відмінні від нуля, то система (3) не сумісна.
Очевидно, що випадок, коли ![]() буде автоматично виключений, якщо додатково вимагати, щоб серед коефіцієнтів при невідомих х і у в системі рівнянь (1) був хоч би один відмінний від нуля коефіцієнт.
буде автоматично виключений, якщо додатково вимагати, щоб серед коефіцієнтів при невідомих х і у в системі рівнянь (1) був хоч би один відмінний від нуля коефіцієнт.
Ми довели наступну теорему.
Якщо коефіцієнти при невідомих і вільних членів системи рівнянь (1) відповідно пропорційні і серед коефіцієнтів при невідомих є хоч би один коефіцієнт, відмінний від нуля, то система рівнянь (1) має нескінченну кількість розв’язків. Всі вони виходять як розв’язок одного й того ж рівняння, яке містить відмінний від нуля коефіцієнт при невідомому.
Розв’яжемо систему рівнянь
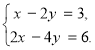
Коефіцієнти при невідомих і вільні члени цієї системи рівнянь відповідно пропорційні. Тому всі розв’язки цієї системи можна отримати як розв’язки одного лише першого рівняння х2у=3.
Припускаючи, що х=t, знаходимо:![]() Отже, дана система рівнянь має безліч розв’язків:
Отже, дана система рівнянь має безліч розв’язків:![]() , де t будь-яке число. Власне, при t=0 маємо розв’язок х=0, у=
, де t будь-яке число. Власне, при t=0 маємо розв’язок х=0, у=![]() при t=5 розв’язок х=5, у=1 і т. д.
при t=5 розв’язок х=5, у=1 і т. д.
Доведену вище теорему корисно сформулювати і в термінах визначників.
Якщо коефіцієнти при невідомих і вільні члени системи рівнянь (1) відповідно пропорційні, то, як легко отримати безпосередньо, використовуючи (2),
![]()
5. Розв’язування систем лінійних однорідних рівнянь
з n-невідомими.
Системи лінійних однорідних рівнянь з n-невідомими розв’язуються методом послідовного виключення невідомих або методом Гаусса.
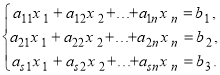
![]() (1)
(1)
Нехай дана довільна система лінійних рівнянь (1).
Припустимо, для визначеності , що коефіцієнт ![]() , хоча насправді він може, звичайно, дорівнювати нулю, і ми повинні будемо почати з якого- небудь іншого, відмінного від нуля, коефіцієнта зпершого рівняння.
, хоча насправді він може, звичайно, дорівнювати нулю, і ми повинні будемо почати з якого- небудь іншого, відмінного від нуля, коефіцієнта зпершого рівняння.
Перетворимо тепер систему (1) , виключаючи невідоме x![]() всіх рівнянь, крім першого . Для цього обидві частини першого рівняння помножемо на число
всіх рівнянь, крім першого . Для цього обидві частини першого рівняння помножемо на число ![]() і віднімемо із відповідних частин другого рівняння, потім обидві частини першого рівняння, помножені на
і віднімемо із відповідних частин другого рівняння, потім обидві частини першого рівняння, помножені на ![]() , віднімемо із відповідних частин третього рівняння, і т. д.
, віднімемо із відповідних частин третього рівняння, і т. д.
Ми отримаємо цим шляхом нову систему іх s лінійних рівнянь з n
невідомими:![]()
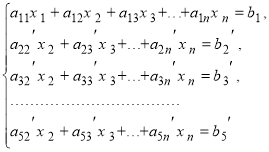 (2)
(2)
Нам немає необхідності явно записувати вирази нових коефіцієнтів
![]() і нових вільних членів
і нових вільних членів ![]() через коефіцієнти і вільні члени вихідної системи (1).
через коефіцієнти і вільні члени вихідної системи (1).
Як ми знаємо, система рівнянь (2) еквівалентна системі (1).
Перетворимо систему (2). При цьому перше рівняння ми не будемо більше чіпати зовсім і підлягаючій перетворенню будемо вважати лише частину системи (2), що складається із всіх рівнянь, крім першого .При цьому ми вважаємо, звичайно , що серед цих рівнянь немає таких , всі коефіцієнти лівих частин, яких дорівнюють нулю, бо такі б рівняння ми б викинули, якщо б їхні вільні члени дорівнювали нулю , а в протилежному випадку ми б уже довели несумісність нашої системи.
Таким чином, серед коефіцієнтів ![]() є відмінні від нуля; для визначеності припустимо, що
є відмінні від нуля; для визначеності припустимо, що ![]() Перетворимо тепер систему(2), віднімаючи від обох частин третього і кожного з наступних рівнянь обидві частини другого рівняння, помножені відповідно на числа
Перетворимо тепер систему(2), віднімаючи від обох частин третього і кожного з наступних рівнянь обидві частини другого рівняння, помножені відповідно на числа
![]()
![]()
Цим буде виключене невідоме ![]() із всіх рівнянь , крім першого і другого , і ми прийдемо до слідуючої системи рівнянь , еквівалентної системі (2) , а тому і системі (1):
із всіх рівнянь , крім першого і другого , і ми прийдемо до слідуючої системи рівнянь , еквівалентної системі (2) , а тому і системі (1):
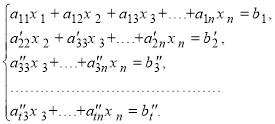
Наша система містить тепер t рівнянь , t s , так як деякі рівняння опинились , мабуть , відкинутими . Зрозуміло , що число рівнянь системи могло зменшитись вже після виключення невідомого ![]() . В майбутньому підлягає перетворенню лише частина одержаної системи , що містить всі рівняння, крім двох перших.
. В майбутньому підлягає перетворенню лише частина одержаної системи , що містить всі рівняння, крім двох перших.
Коли зупиниться цей процес послідовного виключення невідомих ?
Якщо ми прийдемо до такої системи , одне з рівнянь якої має відмінний від нуля вільний член, а всі коефіцієнти лівої частини дорівнюють нулю, то , як ми знаємо , наша вихідна система несумісна.
РОЗВ’ЯЗУВАННЯ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ
Застосування теореми Вієта до розв’язування систем
Якщо у системі рівняння подані у вигляді суми й добутку деяких змінних, то ці змінні є коренями зведеного квадратного рівняння, тобто для розв’язування цієї системи застосовуємо теорему Вієта. ![]()
![]()
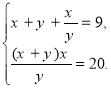
У першому рівнянні системи є сума змінних ![]() а в другому їх добуток
а в другому їх добуток ![]() Отже, ці змінні є коренями квадратного рівняння
Отже, ці змінні є коренями квадратного рівняння 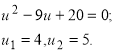
Таким чином,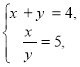 або
або 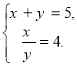
З першої системи x=5y і 5y+y=4, 6y=4, ![]()
З другої системи x=4y і 4y+y=5, 5y=5,![]()
Відповідь:( ![]() ); (4;1).
); (4;1).
Окремі системи рівнянь розв’язуються за допомогою теореми Вієта тільки після попереднього здійснення перетворень. Наприклад, у системі рівнянь
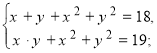
після почленного віднімання рівнянь системи дістанемо:
x+yxy=1,
x+y=xy1.
Після піднесення до квадрата обох частин останнього рівняння матимемо:
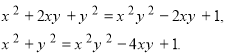
Підставимо ![]() у друге рівняння даної системи рівнянь
у друге рівняння даної системи рівнянь
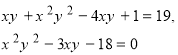
![]()
![]()
квадратне рівняння відносно xy.
![]()
xy=6 або xy=3.
Тоді ![]()
![]()
або ![]() а
а ![]()
або x+y=1822=4.
Таким чином, дана система рівнянь рівносильна системам
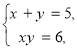 або
або 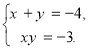
З першої системи рівнянь маємо розв’зки (2;3), (3;2).
З другої системи рівнянь знайдемо розв’язки за теоремою Вієта, розв’язавши рівняння ![]()
![]() Розв’язки даного рівняння:
Розв’язки даного рівняння:![]()
Одночасно вони є розв’язками даної системи.
Відповідь: (2;3); (3;2); ![]()
Спеціальний прийом розв’язування деяких
систем рівнянь
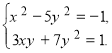
Зауважимо, що у лівій частині обох рівнянь системи є многочлени другого степеня відносно змінних y та x, а у правих частинах обох рівнянь є число. Такі системи рівнянь розв’язують спеціальним прийомом.
Подамо змінну y=tx, де t-деяке дійсне число, відмінне від нуля, і підставимо в кожне рівняння системи:
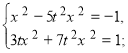
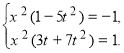
Поділимо почленно рівняння системи і позначимо t:
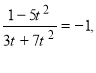
![]()
![]()
![]()
Отже, y = x або ![]()
Підставимо y = x у перше рівняння даної системи:
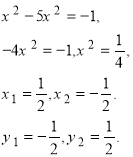
Підставимо ![]() у перше рівняння даної системи:
у перше рівняння даної системи:
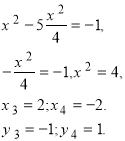
Відповідь:![]()
Розв’язування систем ірраціональних рівнянь

Ліву частину першого рівняння даної системи можна подати у вигляді добутку коренів: ![]()
Тоді дана система рівнянь рівносильна системі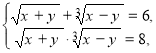
у якій є сума змінних і їх добуток. За теоремою Вієта
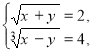 або
або 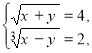
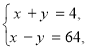
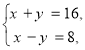
2x=68, 2x=24,
x=34, x=12,
y=30. y=4.
Відповідь: (34; 30);(12;4).
Розв’яжемо іншу систему ірраціональних рівнянь.
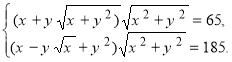
Ліві частини рівнянь системи запишемо у вигляді:
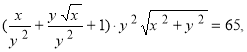
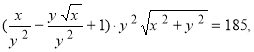
Поділимо почленно рівняння системи:
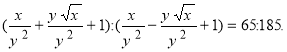
Спростивши цю рівність, дістанемо:
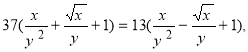
звідки 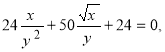
або 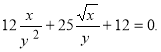
Вводимо нову змінну ![]() Дістанемо:
Дістанемо:
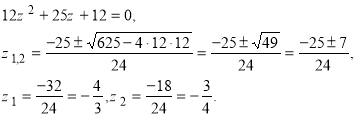
Візьмемо ![]() і знайдемо
і знайдемо![]() .
.
Маємо ![]() =
=![]() звідки
звідки ![]() Підставимо значення
Підставимо значення 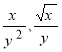 і
і ![]() у перше рівняння системи
у перше рівняння системи ![]()
![]() звідки
звідки ![]()
![]()
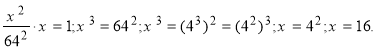
Знайдемо y. Маємо:![]()
![]() звідки y=3. Аналогічно, підставляючи значення
звідки y=3. Аналогічно, підставляючи значення
![]()
![]() знайдемо x=9,y=4.
знайдемо x=9,y=4.
Відповідь:(16;3),(9;4).
Розв’язування систем логарифмічних рівнянь.
1. Розв’яжемо систему рівнянь.
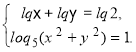
Система рівнянь має зміст, якщо х >0, y>0.
За правилами логарифмування рівняння lqx + lqy = lq2 можна змінити
рівнянням xy = 2. А за означенням логарифма loq5 (x![]() +y
+y![]() )=1 можна
)=1 можна
замінити рівнянням x ![]() +y
+y![]() = 5 . Дана система рівнянь рівносильна системі
= 5 . Дана система рівнянь рівносильна системі ![]()
![]()
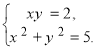
Нехай у = tx. Тоді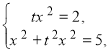
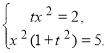
Поділимо почленно рівняння системи й визначимо t.
![]()
![]() 2t
2t![]() 5t+2=0, t=
5t+2=0, t=![]()
t1=2, t2=![]() . Отже, у=2x або y =
. Отже, у=2x або y =![]() x.
x.
Підставимо у =2x у рівняння xу = 21, 2x![]() =2,
=2,
x = 1, у = 2.
Підставимо у=![]() x у рівняння ху =2;
x у рівняння ху =2; ![]() =2, x
=2, x ![]() =4, x =2, у =1.
=4, x =2, у =1.
Відповідь. (1; 2), (2; 1),
2.Розв’яжемо іншу cистему рівнянь. 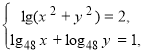
Cистема має зміст , якщо x>0 , y>0.
До лівої частини другого рівняння системи застосовуємо властивість
логарифма добутку і використаємо означення логарифма до обох рівнянь системи . Дістанемо:
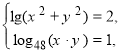
![]()
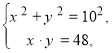
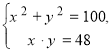
Застосування методу підстановки досить громіздке .
Спробуємо дістати суму змінних .Для цього друге рівняння утвореної
системи помножимо на 2 і додамо почленно до першого рівняння .
Матимемо x![]() +2 xy + y
+2 xy + y![]() = 100 +96 ,
= 100 +96 ,
(x+y) ![]() = 196,
= 196,
x+y = 14 , бо x>0 , y>0 .
Отже , утворена система рівнянь рівносильна системі
![]()
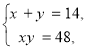
звідки x1 = 6 , y1 = 8 або x2 = 8 , y2 = 6 (за теоремою Вієта ).
Відповідь : (6; 8), (8; 6).
Розв’язування систем показникових рівнянь.
Розв’яжемо систему рівнянь.
![]()
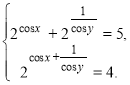
![]()
За зворотною властивістю множення степенів за однаковими основами
друге рівняння системи можна подати у вигляді![]()
Тоді дана система рівнянь матиме вигляд
![]()
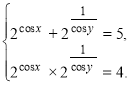
![]()
2![]() і 2
і 2![]() є коренями квадратного рівняння t
є коренями квадратного рівняння t![]() 5t + 4 = 0: t1 = 1, t2 = 4.
5t + 4 = 0: t1 = 1, t2 = 4.
Oтже,
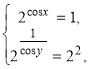
![]() або
або 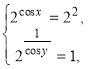
звідки


x=![]()
y=![]()
А система рівнянь
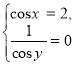
не має змісту.
Відповідь. (nk), де n, k
Розв’язування комбінованих систем рівнянь.
Розв’яжемо систему рівнянь
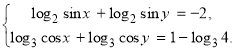
Система рівнянь має зміст, якщо одночасно виконуються умови :
sin x>0, сos x>0, sin y>0,cos y>0,тобто x і y містяться у першій координатній чверті.
Подамо суми логарифмів як логарифми добутків.
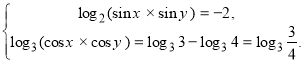 За означенням логарифма і властивістю оборотності логарифмічної функції маємо:
За означенням логарифма і властивістю оборотності логарифмічної функції маємо:
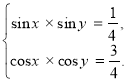
Після почленного додавання й віднімання рівнянь системи дістанемо:
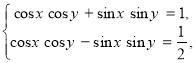
![]()
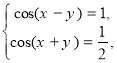
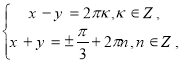
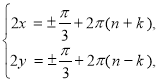
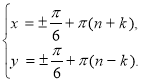
Але числа x і y повинні належати першій координатній чверті .
Виберемо їх з останньої системи рівнянь:
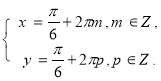
Відповідь: (m p , m,p.
Системи тригонометричних рівнянь.
Розв’яжемо систему рівнянь
![]()
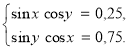
Почлено додаємо і віднімаємо рівняння даної системи
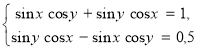
і застосовуємо формули синуса суми й різниці двох чисел
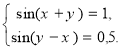
Дістали найпростіші тригонометричні рівняння 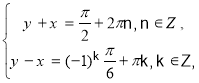
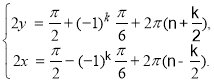
x=![]() nk
nk
y=+![]() n+k n, k.
n+k n, k.
Відповідь: Пари чисел (![]() nk;+
nk;+![]() n+k) n, k.
n+k) n, k.
Зауважуємо, що при розв’язуванні системи значення цілих чисел у формулах розв’язків кожного з рівнянь системи слід брати різними.
Якщо лише одне рівняння системи тригонометричне , то й у цьому випадку її називають системою тригонометричних рівнянь.
КРУГОВІ СИСТЕМИ
Круговими системами перщого типу називаються такі системи, в яких при дуговій перестановці ліва частина першого рівняння переходить в ліву частину другого рівняння, ліва частина другого рівняння в ліву частину третього, а ліва частина третього в першу. Універсальний метод розв’язування таких рівнянь це зведення їх до найпростіших кругових систем.
Перший тип
1) Коли рівняння лінійні
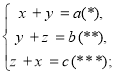
![]()
Додамо почлено рівняння
2(x+y+z)=a+b+c,
x+y+z=![]() (1)
(1)
z=(1) (*) z=![]() z=
z=![]()
x=(1)(**) x=![]() x=
x=![]()
y=(1)(***) y=![]() y=
y=![]()
Другий тип.
2) ![]()
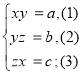 Перемножимо почлено рівняння
Перемножимо почлено рівняння
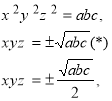
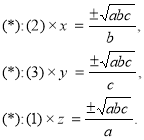
![]()
![]()
Кругові системи другого виду,це системи в яких при круговій перестановці перше рівняння переходить в друге, друге в третє і третє в перше.
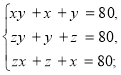
Якщо кругова система другого виду має розв’язки,то цими розв’язками є числа x=z=y
1 cпосіб
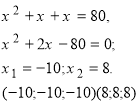
![]()
2 спосіб
Другий спосіб полягає у почленому відніманні рівнянь.
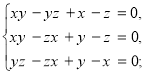
![]()
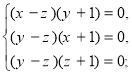
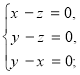
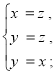 x=y=z
x=y=z
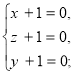
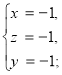 сторонній корінь.
сторонній корінь.
Загальний метод розв’зання кругових систем 2-го виду.
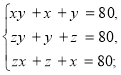
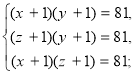
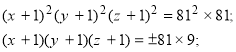
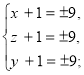
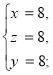
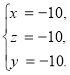
СИМЕТРИЧНІ СИСТЕМИ
Симетричними системами з двома змінними називаються системи, в яких при заміні однієї зміної на іншу кожне рівняння системи не змінюється.
![]()
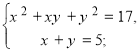 (2;3) (3;2)
(2;3) (3;2)
У симетричних систем, якщо пара (a;b) є розв’язками системи, то розв’язком цієї системи є і пара (b;a).
Часто розв’язки таких систем можна знайти за допомогою введення нових змінних - елементарних симетричних многочленів ![]()
![]()
Знайти розв’язки системи
![]()
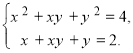 (1)
(1)
Введемо нові змінні - елементарні симетричні многочлени
![]()
Відносно змінних ![]() систему (1) запишемо у вигляді
систему (1) запишемо у вигляді
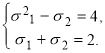 (2)
(2)
Визначивши ![]() з другого рівняння через
з другого рівняння через ![]() :
:
![]() =2 -
=2 - ![]() (3)
(3)
підставивши ![]() =2 -
=2 - ![]() в перше рівняння системи (1), дістанемо квадратне рівняння
в перше рівняння системи (1), дістанемо квадратне рівняння ![]() корені якого дорівнюють 2 і - 3.
корені якого дорівнюють 2 і - 3.
Підставивши знайдені значення ![]() в рівність (3) , дістанемо значення
в рівність (3) , дістанемо значення ![]() . Отже, множина розв’язків системи (1) має вигляд
. Отже, множина розв’язків системи (1) має вигляд
![]() =2,
=2, ![]() =0;
=0; ![]() =-3,
=-3, ![]() =5.
=5.
Тепер множину розв’язків початкової системи (1) можна знайти як об’єднання множин двох простих систем

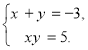
Друга система розв’язків не має. Розв’язками першої системи є пари чисел ![]()
Висновок
Як і всі інші науки, математика виникла з практичних потреб людства: з вимірювання площ земельних ділянок і місткості посудин, з обчислення часу та механіки. Але найбільш практичне застосування, на мою думку, має розв’язування рівнянь та систем рівнянь.
Вивчення рівнянь починається з дуже простого випадку, одного рівняння першого ступеня з одним невідомим, а потім розвиваються в двох напрямах. З одного боку, розглядаються системи двох і трьох рівнянь першого ступеню з двома і, відповідно , з трьома невідомими; з іншого боку, вивчається одне квадратне рівняння з одним невідомим, а також окремі випадки типів рівнянь більш високого ступеню.
Один з цих напрямків, а саме основи лінійної алгебри, має вихідною задачею вивчення довільних систем рівнянь першого ступеня , тобто лінійних рівнянь. Для розв’язування таких систем, в тому випадку, коли число рівнянь дорівнює невідомих, розробляється апарат теорії визначників, наведений вище.
Сучасна математика не може існувати без розв’язування рівнянь та систем рівнянь.Такий розділ фізики , як механіка, взагалі не можна уявити без розв’язування рівнянь та систем рівнянь. Деякі геометричні задачі можна розв’язати лише за допомогою систем рівнянь. Так, наприклад, перетин двох фігур, заданих рівняннями, можна знайти тільки розв’язавши систему рівнянь.
ЛІТЕРАТУРА
1. О.С.Теляковський. “ Алгебра”- К.”Освіта”1994
2. Є.С.Кочетков, Є.С.Кочеткова. “ Алгебра та елементарні функції”.Ч.1- М.”Просвещение”1974
3. Г.П.Бевз ”Алгебра”-К.”Освіта”1996
4. А.Г.Курош.”Курс вищої алгебри”-М.”Наука”1971
5. О.Г.Ципкін.”Довідник з математики”-K.”Вища школа”1988


про публікацію авторської розробки
Додати розробку
