«РОЗВ’ЯЗУВАННЯ ТРИКУТНИКІВ»

     ПРИКЛАДНІ ЗАДАЧІ, ЯКІ МОЖНА ВИКОРИСТОВУВАТИ ПРИ ВИВЧЕННІ ТЕМИ «РОЗВ’ЯЗУВАННЯ ТРИКУТНИКІВ» У 9 КЛАСІ.

   Радіопеленгатор  —  радіоприймач з особливою (рамкою) антеною, за допомогою якої визначається пеленг на радіомаяк.

Радіомаяк — радіостанція з відповідним режимом роботи, пеленгуючи яку, судна визначають лінію положення (напрямок на маяк).

   Радіонавігація — судноводіння за допомогою радіоелектронних приладів. До радіонавігації відносять визначення місця судна в морі за допомогою так званих фазових радіонавігаційних систем.

   Радіолокаційна станція —  радіотехнічна апаратура, за допомогою якої ведеться спостереження за обстановкою довкола судна. Обстановка висвічується на екрані електронної променевої трубки (індикатор кругового огляду).

РАДІОПЕ́ЛЕНГ.

1. Кут, утворюваний географічним меридіаном і напрямом від радіоприймача на випромінювач радіохвиль.

2. Сигнал передавальної радіостанції, за яким визначається кут між меридіаном і напрямом на цю станцію.

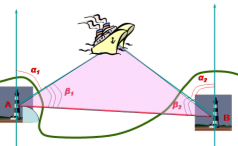
  Знаючи радіопеленг і об'єкта С з двох радіомаяків А і В, можна визначити радіопеленг і об'єкта по відношенню до лінії АВ. Це дозволяє звести задачу спостереження за об'єктом С до задачі розв'язання трикутника АВС.

Методи і засоби радіолокації застосовуються

• у військовій справі (ППО, точність стрільби);
•  в морській, повітряній і космічній навігації;
• в сейсмології;
• в метеорології;
• при розвідці корисних копалин;
•  при охороні об'єктів;
• в медицині.

 

 

Задача1

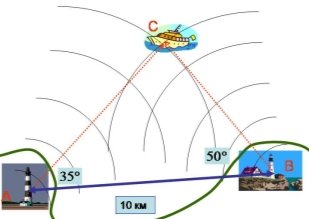
 В умовах поганої видимості з берегових радіомаяків А і В, відстань між якими дорівнює 10 км,запеленгували судно С. Визначте відстань від судна до кожного маяка, якщо за допомогою радіопеленгаторів визначені кути: САВ =35° і СВА =50°.

Розв’язання.

1)               

2) ВС=; ВС=             

3)АС=; АС=              

  Відповідь:ВС. 

 

Задача 2

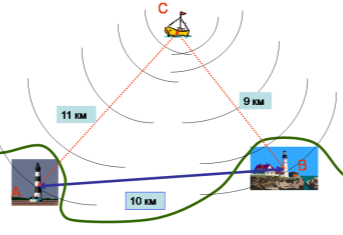
  Берегові радіомаяки А і В розташовані на відстані 10 км. З судна С за допомогою радіолокаційної станції, що знаходиться на ній, визначені відстані до маяків СА = 11 км і СВ = 9 км. Знайдіть кути САВ і СВА пеленгів радіомаяків.

Розв’язання.

1. 

          

 

2. 

 

   Відповідь:

Задача 3.

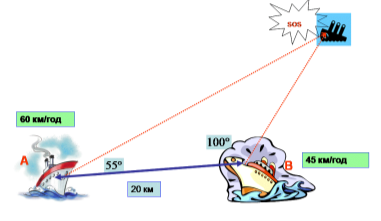
Два теплоходи А і В знаходяться в відкритому морі на відстані 20 км один від другого, одночасно отримали  сигнал біди з потопаючого корабля С.

Радіопеленг стосовно лінії АВ на судні А дорівнює 55 °, а на судні В - 100°. Хто першим прийде на допомогу, якщо максимальна швидкість судна А –

60 км / год, судна В - 45 км / год?

Розв’язання.

1)                               

2) АС=         

,

3)ВС=     

           

 5)

Відповідь:теплохід А прибуде на допомогу на 5хв раніше.

 

Задача 4

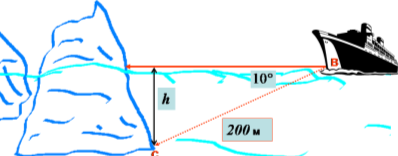По курсу криголама В виявлений айсберг.  З допомогою ультразвукового ехолота під максимальним кутом 10 визначена підводна точка C айсберга на відстані 200 м. Визначте глибину h підводної частини айсберга.

Розв’язування.

 AC=BC   

Відповідь: АС34м.

 

Задача 5

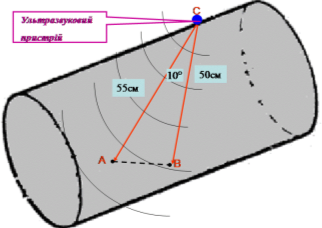При дослідженні металевої деталі методом ультразвукової локації була виявлена внутрішня тріщина. Визначте довжину тріщини АВ, якщо відстані від кордонів тріщини до ультразвукового пристрою С рівні

 50 см і 55 см, а

 кут АСВ дорівнює 10.

 

Розв’язання.

     

АВ=10,4 см.

Відповідь: довжина тріщини 10,4 см.

 

 

 

 

 

 

Задача 6.

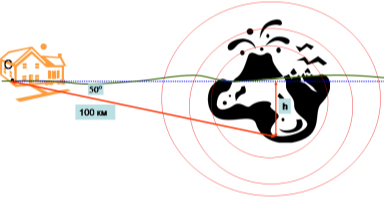Сейсмічною станцією С зафіксовані сильні підземні поштовхи на відстані 100 км від станції під кутом 50 до поверхні землі. Визначте глибину епіцентру землетрусу h.

 

Розв’язання.

h=AB=BC          

h=100.

Відповідь: епіцентр землетрусу знаходиться на глибині 77км.

                                     Задача 7

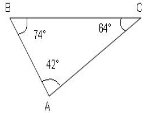
Для знаходження відстані від точки А до дзвіниці В, яка розташована на іншому березі річки (рис.), за допо­могою віх, рулетки і приладу для вимірювання кутів (теодоліту) позначили на міс­цевості точку С таку, що ВАС = 42°, АСВ = 64°, АС - 20 м. Як знайти від­стань від А до В? Знайдіть цю відстань.

Розв’язання.

За теоремою синусів маємо:

=

Відповідь: відстань до дзвіниці В 18,7 метра.

 

Задача 8.

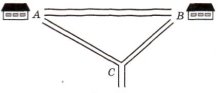Дороги із сіл А і В сходяться біля розвилки С (рис.). Дорога із села А до розвилки утворює з дорогою в село В кут у 30°, а дорога із села В з дорогою в село А — кут у 70°. Одночасно із села А до розвилки виїхав автомобіль зі швидкістю 90 км/год, а із села В — автобус зі швидкістю 60 км/год. Хто з них першим доїде до розвилки?

Розв’язання.

Швидкість автомобіля (V₁)  90 км/год. Автомобіль рухається по шляху АС швидкість автобуса (V₂) 60 км/год, автобус рухається по шляху ВС.

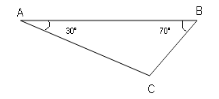Знайдемо час руху автомобіля і автобуса та порівняємо їх.

t₁=;     t₂=;

За теоремою синусів

;    AC= BC

               t₁= ;       t₂=;        =>t₁>t₂

Оскільки час руху автобуса менший, то автобус до розвилки доїде першим.

Відповідь: Автобус.