УРОК 4

Тема уроку.   Існування площини, яка проходить через три дані точки.

Мета уроку:   вивчення теореми про існування єдиної площини, яка

проходить через три дані точки, які не лежать на одній прямій.

Обладнання: стереометричний набір, моделі куба і тетраедра.

Хід уроку

І. Перевірка домашнього завдання

1. Один із учнів відтворює розв'язування задачі № 10, решта класу пише математичний диктант.

2. Математичний диктант.

Дано зображення тетраедра (варіант 1 — рис. 17, варіант 2 – рис. 18).

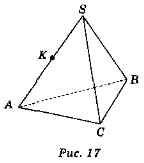
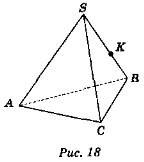
Користуючись зображенням, запишіть:

1) площину, яка проходить через точку Κ і пряму АВ; (2 бали)

2) площини, в яких лежить пряма ВС, (2 бали)

3) точку перетину прямої КС з площиною АВС; (2 бали)

4) пряму перетину площин АВК і АВС; (2 бали)

5) пряму перетину площин ВСК і ASS; (Я бали)

6) прямі, які лежать в площині ACS; (2 бали)

Відповідь.  Варіант 1. 1) ABS: 2) BCS, ВСК, ВСА; 3) С; 4) АВ; 5) KB;

6) AC, КС, CS, AS.

Варіант 2. 1) АВК; 2) BCS, АВС; 3) С; 4) АВ; 5) BS; 6)AC, AS, CS.

3. Обговорення результатів математичного диктанту та розв'язання задачі № 10.

II. Сприйняття й усвідомлення нового матеріалу

Теорема про існування площини, яка проходите через три точки

Нам відомо два способи задання площини: площину можна провести  через дві прямі, які перетинаються, а також через пряму і точку, яка не  належить цій прямій.

Існує третій спосіб.

Теорема.

Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

Учні самостійно знайомляться з доведенням цієї теореми за підручником (с. 6).

Слід звернути увагу учнів на те, що площина однозначно задається трьома точками, які не лежать на одній прямій, і тому в літературі площину, яка проходить через точки А, В, С і С АВ , позначають символом (АВС).

Виконання вправ

1. Чи можуть дві різні площини мати три спільні точки, які не лежать на одній прямій? Відповідь обґрунтуйте.
2. Задача № 3 із підручника (с. 10).
3. Три точки в просторі розміщені так, що через них можна провести не  менше 100 площин. Що можна сказати про розміщення цих точок?
4. Рівно о 12 годині з навчального полігону було запущено три ракети. О котрій годині центри мас цих ракет будуть знаходитися в одній площині?
5. Щоб надати більшої стійкості вимірювальним приладам, їх часто  встановлюють на триногах. На якому теоретичному факті базуються такі дії?
6. Задано три точки А, В, С. Скільки площин можна провести через них, якщо:.

а) АВ = 3 см, ВС = 4 см, АС = 5 см;

б) AВ = 3 см, ВС = 4 ом, АС = 7 см?

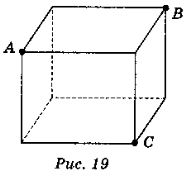
7. Дано зображення куба (рис. 19). Побудуйте переріз куба площиною, яка проходить через точки А, В, С.
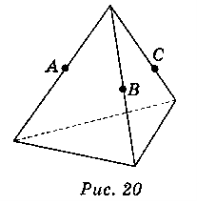
8. Дано зображення трикутної піраміди (рис. 20). Побудуйте переріз  піраміди площиною, яка проходить через точки А, В, С.
9. Через середини трьох ребер куба, які виходять із однієї вершини проведено переріз. Обчисліть периметр і площу перерізу, якщо ребро куба дорівнює 6 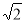см.
10.  У трикутній піраміді, кожне ребро якої дорівнює 4 см, побудовано переріз площиною, яка проходить через середини трьох ребер, що виходять із однієї вершини. Обчисліть периметр і площу утвореного перерізу.

ІІІ. Домашнє завдання

§ 1, п. 4; контрольне запитання № 5; задача № 12 (с. 10).

ІV. Підведення підсумку уроку

Запитання до класу

1. Скільки площин можна провести через три дані точки?
2. У просторі дано три точки А, В, С, які лежать на одній прямій. Визначте, які з наведених тверджень правильні, а які — неправильні:

а) через точки А, В, С можна провести тільки одну площину;

б) через точки Α, В, С можна провести безліч площин;

в) через точки А і В можна провести площину, яка не містить точку С;

г) через А можна провести площину, яка має з прямою ВС тільки одну спільну точку.