УРОК 3

Тема уроку. Перетин прямої з площиною. Перерізи многогранників.

Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника.

Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

1. Фронтальне опитування.

1. Скільки площин визначають дві прямі, які перетинаються?
2. Скільки площин визначають пряма і точка?
3. Скільки площин можна провести через три прямі, які мають спільну точку?
4. Скільки площин можна провести через пряму і дві точки, які не належать їй?

2. Перевірка правильності виконання задачі № 6.

ІІ. Сприйняття й усвідомлення нового матеріалу

Теорема про належність площині прямої, дві точки якої належать площині

Теорема.

Дано: В α, С α (рис. 12).

Довести: ВСα.

Доведення

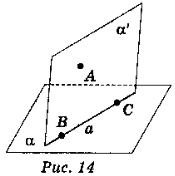Візьмемо точку А, яка не лежить на прямій ВС (згідно з аксіомою І). Через пряму ВС і точку А проведемо площину α`.

Якщо площини α і α` збігаються, то площина α містить пряму ВС (рис. 13).

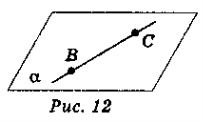
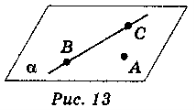
Якщо площини α і α` різні, то вони перетинаються по прямій а, яка містить точки В і С (рис. 14). За аксіомою І прямі а і ВС збігаються, отже, пряма ВС лежить в площині α.

Виконання вправ

1. Доведіть, якщо вершини трикутника АВС належать деякій площині α, то трикутник АВС лежить в цій площині.
2. Доведіть, що чотирикутник АВСD лежить в одній площині, якщо його діагоналі АС і BD перетинаються.
3. Доведіть, що чотирикутник ABCD – плоский, якщо продовження двох протилежних сторін АВ і CD перетинаються.
4. Як перевірити якість виготовлення лінійки за допомогою добре відшліфованої плити?
5. Задача № 9 із підручника (с. 9).
6. Задача № 11 із підручника (с. 10).

Взаємна розміщення прямої і площини

Із доведеної теореми випливає, що площина і пряма, яка не лежить у площині, або перетинаються, або не перетинаються.

Отже, можливі такі випадки взаємного розміщення прямої і площини (схема “Взаємне розміщення прямої і площини”):

а) площина α не має з прямою а спільних точок;

б) площина α має з прямою а одну спільну точку;

в) пряма а лежить у площині α.

Завдання.

На предметах оточуючого простору покажіть різні випадки взаємного розміщення прямої і площини.

Поняття перерізу многогранника

У стереометрії розглядають перерізи многогранників.

Перерізом многогранника називається многокутник, який утворюється при перетині многогранника з площиною. Вершини цього многогранника є точками перетину січної площини з ребрами многокутника, а сторони – частинами прямих перетину січної площини з його гранями.

Для побудови простих перерізів необхідно вміти розв’язувати дві опорні задачі:

1. будувати лінію перетину двох площин;
2. будувати точку перетину прямої і площини.

Для побудови лінії перетину двох площин — січної площини і грані многогранника — знаходять дві точки шуканої прямої і через них проводять пряму.

Виконання вправ

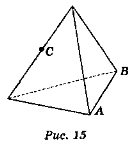
1. Дано зображення трикутної піраміди (рис. 15). Побудуйте переріз піраміди площиною, яка проходить через пряму АВ і точку С.

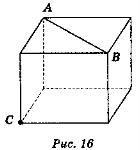
2. Дано зображення куба (рис. 16). Побудуйте переріз куба площи­ною, яка проходить через пряму АВ 1 точку С.

3. У трикутній піраміді SABC всі ребра дорівнюють 10 см. Побудуй­те переріз піраміди площиною, яка проходить через ребро AS і точку Μ — середину ребра ВС. Знайдіть периметр побудовано­го перерізу.

4. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через діагональ ВD верхньої основи і точку Μ — середину ребра АА₁. Обчисліть периметр перерізу, якщо ребро куба дорівнює 10 см.

III. Домашнє завдання

§ 1, π. 3; контрольне запитання № 4; задача .№ 10 (с. 9).

IV. Підведення підсумку уроку

Запитання до класу

1) Що можна стверджувати про пряму, дві точки якої належать даній площині?

2) Точки А і В належать площині α , а точка С лежить поза площиною α . Вкажіть, які з наведених тверджень правильні, а які — неправильні:

а) пряма АС лежить в площині α ;

б) пряма СВ не лежить в площині α ;

в) пряма АВ лежить поза площиною α ;

г) пряма АВ лежить в площині α .