Розв’язування вправ на застосування перетворень виразів
МЕТА: -
- навчальна: узагальнити та систематизувати знання та вміння учнів щодо способів перетворень цілих виразів, набутих учнями в ході вивчення алгебри в 7 класі; систематизувати знання щодо видів завдань, які передбачають застосування цих знань та способів дій; відпрацювати навички класифікації, вибору відповідного способу розв'язання названих видів виразів;
- виховна: виховувати інтерес до вивчення математики, вміння робити висновки;
- розвивальна: розвивати пам'ять, увагу, уміння аналізувати.
ТЕМА: Розв’язування вправ на застосування перетворень виразів
МЕТА: - навчальна: узагальнити та систематизувати знання та вміння учнів щодо способів перетворень цілих виразів, набутих учнями в ході вивчення алгебри в 7 класі; систематизувати знання щодо видів завдань, які передбачають застосування цих знань та способів дій; відпрацювати навички класифікації, вибору відповідного способу розв'язання названих видів виразів;
- виховна: виховувати інтерес до вивчення математики, вміння робити висновки;
- розвивальна: розвивати пам'ять, увагу, уміння аналізувати.
ТИП УРОКУ: узагальнення та систематизація знань.
ПЛАН УРОКУ
- Організаційний етап. (1-2 хв.)
- Перевірка домашнього завдання. (3-4 хв.)
- Актуалізація опорних знань учнів. (4-5 хв.)
- Систематизація й узагальнення знань та вмінь.(9-10 хв.)
- Засвоєння вмінь та навичок. (14-15 хв.)
- Домашнє завдання. (3-4 хв.)
- Підбиття підсумків уроку. (4-5 хв.)
ХІД УРОКУ
І. Організаційний етап.
1.1. Привітання.
1.2. Фіксація відсутніх учнів.
1.3. Перевірка готовності учнів до уроку.
ІІ. Перевірка домашнього завдання.
Перевірка наявності виконаного домашнього завдання та відповіді на запитання, які виникли в учнів при його виконання.
ІІІ. Актуалізація опорних знань учнів.
Виконання усних вправ
-
Укажіть знак виразу:
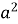 ;
; ;
; 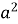 + 7;
+ 7;  + 3;
+ 3; 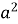 +
+ 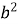 + 3;
+ 3;  ;
;  + 3.
+ 3.
-
Якого найменшого значення набуває вираз:
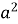 ;
;  ;
; 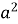 + 7;
+ 7;  – 3;
– 3;
![]() +
+ ![]() + 3;
+ 3; ![]() ;
; ![]() + 3?Чому?
+ 3?Чому?
-
Який знак має вираз: -
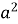 ; -
; - ; -
; -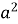 - 7; -
- 7; - – 3; -
– 3; -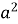 -
- 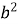 - 3?
- 3?
- Якого найбільшого значення набувають вирази в п. 3? При яких значеннях змінних це відбувається?
Висновок. Запам'ятаймо, що
1) (А)2 ≥ 0, отже, (А)2+В ≥ В, тобто (А)2 = 0 при А = 0 і найменше значення виразу (А)2 + В дорівнює В.
2) -(А)2 ≤ 0, отже, -(А)2 + В ≤ В, тобто найбільше значення виразу
-(А)2 +В дорівнює В при А = 0.
IV. Систематизація й узагальнення знань та вмінь.
Ми отримали наступні висновки:
- Квадрат будь-якого виразу є число невід'ємне.
- Квадрат будь-якого виразу дорівнює нулю, якщо цей вираз дорівнює нулю.
- Якщо квадрат деякого виразу змінити на деяке число, значення нового виразу буде відрізнятися від квадрата на це саме число.
- Вираз, протилежний квадрату деякого виразу, є числом не додатним.
Розглянемо наступні приклади на підтвердження отриманих результатів:
Приклад 1. Доведіть, що вираз ![]() набуває лише додатних значень при будь-яких
набуває лише додатних значень при будь-яких ![]()
![]()
Доведення
Виділивши із тричлена ![]() квадрат двочлена, матимемо:
квадрат двочлена, матимемо:
![]() .
.
Ми подали многочлен у вигляді суми двох доданків ![]() . Доданок
. Доданок ![]() для будь яких
для будь яких ![]()
![]() набуває лише додатних значень. Оскільки
набуває лише додатних значень. Оскільки ![]() , то й вираз
, то й вираз ![]() набуває лише додатних значень.
набуває лише додатних значень.
Виходячи з рівності ![]() можна вказати найменше значення многочлена
можна вказати найменше значення многочлена ![]() . Воно дорівнює 2, до того ж, цього найменшого значення многочлен набуває, якщо
. Воно дорівнює 2, до того ж, цього найменшого значення многочлен набуває, якщо ![]()
Приклад 2. Знайти найбільше значення многочлена![]() .
.
Розв’язання
![]() .
.
Найбільше значення многочлена дорівнює 5.
Приклад 3. Довести, що значення виразу ![]() ділиться на 8 для будь-якого цілого значення
ділиться на 8 для будь-якого цілого значення ![]()
Розв’язання
Спростимо даний вираз
![]()
![]() .
.
Для будь-якого цілого значення ![]()
![]()
![]() ділиться на 8.
ділиться на 8.
V. Застосування знань та вмінь
- Доведіть, що вираз набуває лише невід’ємних значень:
а) ![]() ; б)
; б) ![]() .
.
Розв’язання
а) ![]()
Доданок ![]() для будь яких
для будь яких ![]()
![]() , то й вираз
, то й вираз ![]() набуває лише додатних значень.
набуває лише додатних значень.
б) ![]()
Доданок ![]() для будь яких
для будь яких ![]()
![]()
![]() набуває лише додатних значень. Оскільки
набуває лише додатних значень. Оскільки ![]() , то й вираз
, то й вираз
![]() набуває лише додатних значень.
набуває лише додатних значень.
- Доведіть, що значення виразу ділиться на дане число.
а) ![]() на 9; б)
на 9; б) ![]() на 500;
на 500;
в) ![]() на 16.
на 16.
Розв’язання
а) ![]() на 9;
на 9;
![]()
Добуток ![]()
![]() ділиться на 9.
ділиться на 9.
б) ![]() на 500;
на 500;
![]() .
.
Добуток ![]()
![]() ділиться на 500.
ділиться на 500.
в) ![]() на 16;
на 16;
![]() .
.
Добуток ![]() ділиться на 16, а тому й
ділиться на 16, а тому й ![]() ділиться на 16.
ділиться на 16.
- За допомогою мікрокалькулятора знайдіть значення многочлена:
а) ![]() , якщо
, якщо ![]()
б)![]() , якщо
, якщо ![]()
в) ![]() , якщо
, якщо ![]()
Розв’язання
а) ![]() , якщо
, якщо ![]()
![]()
![]()
б)![]() , якщо
, якщо ![]()
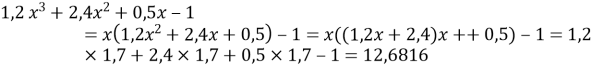 .
.
в) ![]() , якщо
, якщо ![]()
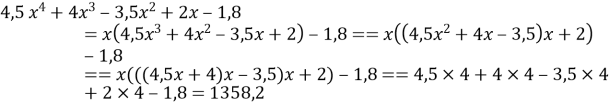 .
.
VI. Завдання додому
- Доведіть, що вираз набуває лише невід’ємних значень:
а) ![]() ; б)
; б) ![]() .
.
Розв’язання
а) ![]() .
.
Доданок ![]() для будь яких
для будь яких ![]()
![]() , то й вираз
, то й вираз ![]() набуває лише додатних значень.
набуває лише додатних значень.
б) ![]() .
.
Доданок ![]() для будь яких
для будь яких ![]()
![]()
![]() набуває лише додатних значень. Оскільки
набуває лише додатних значень. Оскільки ![]() , то й вираз
, то й вираз
![]() набуває лише додатних значень.
набуває лише додатних значень.
- Доведіть, що значення виразу ділиться на дане число:
а) ![]() на 99.
на 99.
Розв’язання
а) ![]() на 99;
на 99;
![]() .
.
Добуток ![]()
![]() ділиться на 99.
ділиться на 99.
- За допомогою мікрокалькулятора знайдіть значення многочлена:
а) ![]() , якщо
, якщо ![]()
б) ![]() , якщо
, якщо ![]()
Розв’язання
а) ![]() , якщо
, якщо ![]()
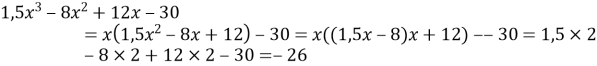 .
.
б) ![]() , якщо
, якщо ![]()
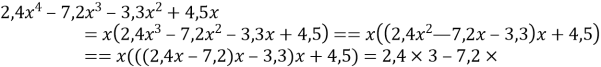
![]()
VIІ. Підбиття підсумків уроку.
З’ясування, які завдання викликали труднощі, відповіді на запитання учнів.
Складаємо схему.



про публікацію авторської розробки
Додати розробку
