Тема уроку. Розв'язування задач з теми «Паралельність прямих і площин». 

Мета уроку: узагальнення й систематизація знань, умінь і навичок учнів з теми «Паралельність прямих і площин».

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

1. Два учні відтворюють розв'язування задач № 39, 40, а в цей час клас пише математичний диктант.

2. Математичний диктант.

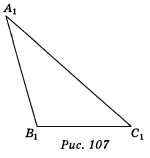
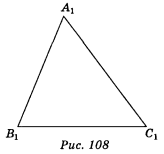
Задано паралельну проекцію A₁B₁C₁

(варіант 1 — рис. 107; варіант 2 — рис. 108) рівнобедреного трикутника АВС (АВ = АС ≠ ВС).

1. Побудуйте проекцію D₁ точки D, яка є серединою відрізка АС. (2 бали)
2. Побудуйте проекцію C₁F₁ медіани CF трикутника АВС. (2 бали)
3. Побудуйте проекцію А₁К₁ бісектриси АК трикутника АВС. (2 бали)
4. Побудуйте проекцію середньої лінії трикутника, яка паралельна стороні ВС. (2 бали)
5. Чи можна відрізок B₁D₁ вважати проекцією висоти трикутника АВС? (2 бали)
6. Чи можна відрізок D₁K₁ вважати проекцією середньої лінії DK? (2 бали)

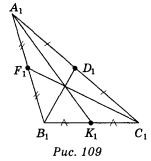
Відповідь. Варіант 1. 1—4) — рис. 109; 5) ні; 6) так.

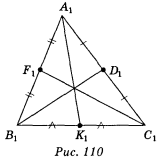
             Варіант 2. 1—4) — рис. 110; 5) ні; б) так.

3. Перевірка виконання математичного диктанту, заслуховування уч­нів, які відтворювали розв'язування задач № 39, 40, та відповіді на запитання, які виникли в учнів при виконанні цих задач та на­писанні математичного диктанту.

II. Закріплення та осмислення знань учнів

Розв'язування задач

1. Паралелограм ABCD не має спільних точок з площиною α. Через точки А, В, С, D проведено паралельні прямі, які перетинають пло­щину а відповідно в точках А₁, В₁, С₁, D₁.

а) Що можна сказати про площини АВВ₁A₁ і CDD₁C₁ ?

б) Визначте вид чотирикутника A₁B₁C₁D₁.

2. Дано паралельні площини α і β. Через точку S, яка не належить жодній із них, проведено прямі а і b, які перетинають площину α в точках A₁ і B₁, а площину β — в точках А₂ і B₂, причому SA₁ = 8 cm, А₁А₂ = 12 cm, A₂B₂ = 25 cm. Знайдіть А₁B₁. (Відповідь. 10 або 50 cm.)
3. Прямі а і b перетинають три дані паралельні площини в точках А₁, А₂, А₃ і В₁, В₂, B₃ відповідно (точка A₂ лежить між точками А₁ і А₃, а точка B₂ — між точками В₁ і B₃). Відомо, що А₁А₂ = 12 см, В₂В₃ = 27 см і А₂А₃ = В₁В₂. Знайдіть довжину відрізків А₁А₃ і В₁В₃. (Відповідь.А₁А₃=30 см, В₁В₃=45 см.)
4. Три паралельні площини перетинають дві мимобіжні прямі в точ­ках A₁, А₂, А₃ і В₁, B₂, B₃ відповідно (точка А₂ лежить між точками A₁ і А₃, точка В₂ — між точками В₁ і B₃). Відомо, що А₂А₃ = 8 см, В₁В₂ = 18 см і А₁A₂ + В₂В₃ ⁼ 24 см. Знайдіть довжини відрізків А₁А₃ і B₁B₃. (Відповідь. А₁А₃ = 20 см, В₁В₃ = 30 см.)
5. Задача № 21* із підручника (с. 20).
6. Задача № 34* із підручника (с. 21).

III. Домашнє завдання

Задачі № 26, 41 (с. 20, 22). Підготувати­ся до тематичної атестації № 2.

IV. Підведення підсумку уроку

Запитання до класу

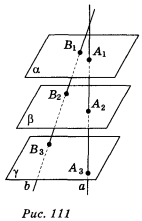
1. Прямі а і b, які перетинаються, перетина­ють три дані паралельні площини α, β, γ в точках А₁, А₂, А₃ і В₁ В₂, В₃ відповідно (рис. 111). Визначте, які з поданих твер­джень правильні, а які — неправильні:

а) прямі А₂В₂ і А₃В₃ мимобіжні;

б) прямі А₁В₃ і А₃В₁ мимобіжні;

в) пряма b і точки А₁, А₂ обов'язково лежать в одній площині;

г) А₁А₃ : A₁A₂  = В₁В₂ : В₁В₃;

д) А₁А₂ : В₁В₂ = A₁A₃ : В₁В₃.

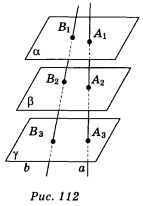
2. Три паралельні площини α, β, γ перети­нають дві дані мимобіжні прямі а і b в точ­ках А₁, А₂, А₃ і В₁, B₂, В₃ відповідно (рис. 112). Укажіть, які з наведених тверд­жень правильні, а які — неправильні:

а) прямі А₁B₃ і В₁А₃ перетинаються;

б) якщо А₂А₃ = 1 см, В₁В₂ = 4 см, А₁A₂ = В₂В₃, то В₁В₃ = 5 см;

в) прямі А₂В₂ і А₃В₃ можуть бути па­ралельними;

г) А₁А₃ : В₁В₃ = А₂А₃ : В₂В₃.