Урок "Розв’язування задач на побудову"
Урок призначенно для проведення у 10 класі. Розглядаеться метод розв'язку екстремальних завдань перетворенням площини. Для раціонального використання навчального часу і підвищення ефективності спільної роботи вчителя і учнів використовується навчальна презентація.
Розв’язування задач на побудову
(екстремальні завдання,10 клас).
Мета:
навчальна: ознайомлення з новим алгоритмом міркувань в аналізі завдань на побудову, створення навичок розв’язування завдань з використанням даного алгоритму.
розвивальна: розвивати навики самоаналізу, самооцінки.
виховна: виховувати упевненість.
Тип уроку: Комбінований урок.
Хід заняття.
1. Організаційний етап.
Постановка мети і завдань заняття.
2. Перевірка виконання домашнього завдання.
Правильність виконання завдання здійснюється за допомогою звірки з наданим рішенням. Обговорення питань.
3. Контроль засвоєння вивченого матеріалу.
Питання: Скільки алгоритмів аналізу завдань на побудову методом перетворення площини знаєте? Назвіть їх.
Відповідь: Чотири.
1) Міркування в аналізі проводяться по алгоритму:
- Умови, що накладаються на шукану фігуру, діляться на дві частини. До першої частини відносяться такі, які є інваріантами деякого перетворення, до другої – всі інші.
- Будується фігура, що задовольняє першій частині умов.
- Перетворенням діють на побудовану фігуру так, щоб знов отримана фігура задовольняла другій частині умов.
2) Для побудови шуканої фігури досить знайти одну її точку A, про яку відомо, що вона належить деякій даній фігурі Ф1 і пов'язана з іншою, не відомою точкою, що належіть іншій даній фігурі Ф2, відомим перетворенням F. В такому разі А належить перетину Ф1 і F(Ф2).
3) При розв’язуванні завдань на побудову з даних елементів шляхом перетворення деяких з них складається допоміжна фігура, яка може бути побудована, а на її основі може бути побудована і шукана фігура.
4) При розв’язуванні використовується той факт, що деякі фігури деяким перетворенням переводяться самі в себе.
4. Вивчення нового матеріалу.
На практиці часто доводиться розв’язувати завдання, пов'язані із знаходженням найбільшої або найменшої відстаней між об'єктами. Це завдання на максимум і мінімум. Одним з методів розв’язування цих завдань є метод перетворення площини. За допомогою електронної презентації розглянемо етапи розв’язування задачі 1.
Комп'ютер дозволяє раціонально використовувати учбовий час (збільшення темпу вивчення нового матеріалу і значне підвищення ефективності спільної роботи вчителя і учнів), сприяє наочності матеріалу, що викладається, забезпечує акуратність, поступальність, можливість швидко повернутися до попереднього фрагмента.
|
Дії вчителя та учнів |
Зображення на екрані |
|
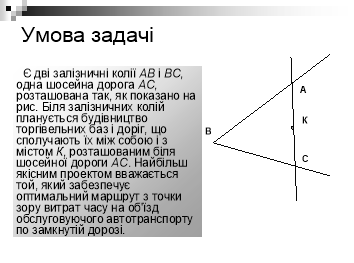
Учитель:Розглянемо наступне завдання: Учні читають, слухають.
|
|
|
Учні читають умови задачі. Учитель: Зверніть увагу, що умова задачі наближена до практичної діяльності людини. Що запропонуєте виконати на 1 етапі розв’язування? Учні відповідають. |
|
|
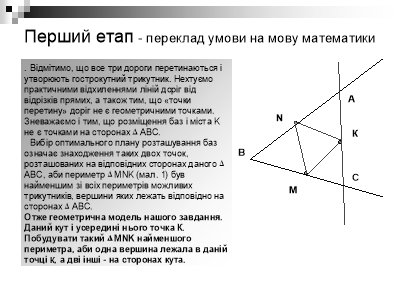
Учні аналізують зміст слайду Вчитель Як сформулювати умову задачі мовою математики? Якими чинниками ми нехтуємо? Учні відповідають
|
|
|
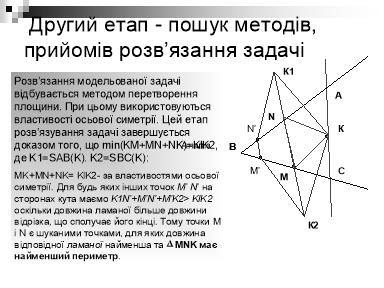
Вчитель Завдяки чому справедливо твердження MK+MN+NK= KlK2 ? Учні відповідають Учні аналізують зміст слайду Вчитель Запропонуйте план побудови розв’язку задачі. Учні відповідають |
|
|
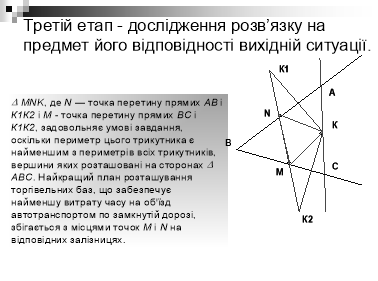
Вчитель Виконуємо побудову |
|
|
Вчитель Чи є інші розв’язки цієї задачі? Чи задовольняє отриманий розв’язок початкову умову задачі?
|
|
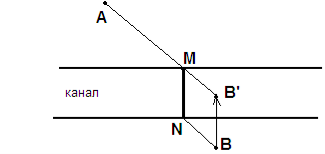 Задача 2. На різних берегах каналу знаходяться населені пункти А і В. В якому місці слід побудувати міст через канал, аби шлях з А у В був мінімальним.
Задача 2. На різних берегах каналу знаходяться населені пункти А і В. В якому місці слід побудувати міст через канал, аби шлях з А у В був мінімальним.
Для розв’язування даного завдання досить знайти образ точки при паралельному перенесенні на вектор ВВ’, який направлений перпендикулярно берегу каналу і має довжину, рівну ширині каналу.
5. Закріплення.
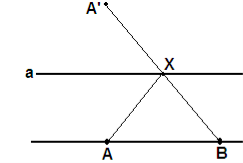 Задача 3. Пряма а паралельна прямій АВ. На прямій а знайдіть таку крапку Х, що ламана АХВ є найкоротшою.
Задача 3. Пряма а паралельна прямій АВ. На прямій а знайдіть таку крапку Х, що ламана АХВ є найкоротшою.
Хід міркувань.
Для розв’язування даного завдання досить знайти образ крапки А при осьовій симетрії з віссю а.
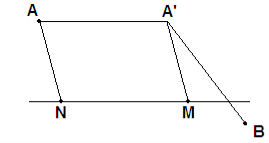 Задача 4. Дано дві крапки А і В по різні сторони від даної прямої а. Відкласти на прямій а відрізок NM, рівний даному відрізку, так, щоб довжина ламаної АNMВ була найменшою.
Задача 4. Дано дві крапки А і В по різні сторони від даної прямої а. Відкласти на прямій а відрізок NM, рівний даному відрізку, так, щоб довжина ламаної АNMВ була найменшою.
Хід міркувань.
Хай ANMB – шукана ламана, відрізок NM має постійну довжину і напрям. Паралельне перенесення NM точку А переводить в А’, отримана ламана AA’MB має ту ж довжину, що і ANMB, і в той же час вочевидь, що її мінімальності можна добитися випрямленням відрізків A’M і МВ.
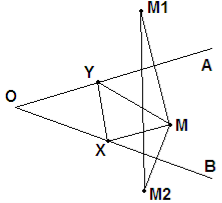 Задача 5. Даний гострий кут і усередині нього точка М. Знайти на сторонах кута такі точки Х і Y, аби периметр трикутника MXY був найменшим.
Задача 5. Даний гострий кут і усередині нього точка М. Знайти на сторонах кута такі точки Х і Y, аби периметр трикутника MXY був найменшим.
Хід міркувань.
Хай XYM – шуканий трикутник, точка Х лежить на промені ОВ, точка Y – на промені ОА. Побудуємо точку М1 – образ точки М при осьовій симетрії з віссю ОА і точку М2 – образ точки М при осьовій симетрії з віссю ОВ. Периметр трикутника MXY дорівнює довжині ламаної М1yxm2, мінімальності якої добиваємося випрямленням.
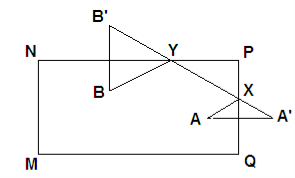 Задача 6. Знайти шлях, якій повинна слідувати більярдна куля, аби ударившись в два борти, пройти з А в В
Задача 6. Знайти шлях, якій повинна слідувати більярдна куля, аби ударившись в два борти, пройти з А в В
Хід міркувань.
Хай MNPQ – більярдний стіл, А і В дані крапки, AXYB – шуканий шлях більярдної кулі. Побудуємо крапку А’ – образ крапки А при осьовій симетрії з віссю PQ і крапку В’ – образ крапки В при осьовій симетрії з віссю NP. Вочевидь, що внаслідок того, що
![]() NYB =
NYB = ![]() PYX =
PYX = ![]() B’YN,
B’YN, ![]() YXP =
YXP = ![]() AXQ = A’XQ і
AXQ = A’XQ і ![]() PYX +
PYX + ![]() YXP = 90°, отримуємо, що точки B’, Y, X, А’ лежать на одній прямій.
YXP = 90°, отримуємо, що точки B’, Y, X, А’ лежать на одній прямій.
6. Рефлексія.
1. Екстремальні задачі – це задачі на пошук
2. У чому полягає метод перетворення площин?
3. З яких етапів складається метод перетворення площин?
7. Домашне завдання.
Завдання: Показати, що зі всіх рівновеликих трикутників із загальною основою найменший периметр має рівнобедрений трикутник.


про публікацію авторської розробки
Додати розробку