Теорема Фалеса у математичному додатку GeoGebra.  

(Геометрія, 8  клас)

 

Мета уроку:

• навчальна: довести теорему Фалеса, навчити застосовувати її при розв’язуванні завдань, окремо за допомогою комп’ютерної програми GeoGebra.
• розвивальна: розвивати в учнів пізнавальний інтерес до учбових дисциплін, уміння застосовувати свої знання з практики.

 

• виховна: виховувати увагу, акуратність, розширювати кругозір учнів.

 

Обладнання:

Комп'ютер, екран, проектор, учнівськи ПК

Навчальна презентація “Теорема Фалеса”, математичний додаток GeoGebra.

 

Хід уроку:

 

І. Організаційний етап

Вітання і вступне слово, визначення мети уроку.

ІІ. Актуалізація опорних знань

Фронтальне опитування учнів (Слайд):

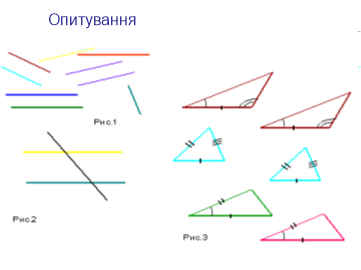
1. Які відрізки називаються рівними?

2. Які прямі називаються паралельними? На рис. 1 покажіть паралельні прямі.

3. Які кути називаються вертикальними, внутрішніми навхрест лежачими? Покажіть їх на рис.2

4. Сформулюйте теорему про властивість паралельних прямих, що перетинаються третьою прямою.

5. Сформулюйте ознаки рівності трикутників. По яких ознаках рівні трикутники на рис 3?

ІІІ. Мотивація навчальної діяльності

Повідомлення теми, завдань та мети уроку.

ІV. Сприйняття та первинне усвідомлення нового матеріалу.

Вчитель пояснює нову тему за допомогою перегляду навчальної презентації “Теорема Фалеса”.

Сьогодні ми доведемо теорему, що носить ім'я старогрецького ученого Фалеса, який жив в 624-547г.г. до н.е.

Великий учений Фалес Мілетський заснував одну з прекрасних наук - геометрію. Відомо, що Фалес Мілетський мав титул один з семи мудреців Греції, що він був воістину першим філософом, першим математиком, астрономом і взагалі першим по всіх науках в Греції. Коротше: він був те ж для Греції, що Ломоносов для Росії.

Кар'єру він починав як купець і ще в молодості попав до Єгипту. У Єгипті Фалес застряг на багато років, вивчаючи науки у Фівах і Мемфісе. Вважається, що геометрію і астрономію до Греції привіз він.

Фалес — математик. Він виміряв по тіні висоту піраміди; встановив, що коло діаметром ділиться навпіл, що кути при підставі рівнобедреного трикутника рівні. Йому ж належить теорема, що вписаний кут, що спирається на діаметр окружности- прямої.

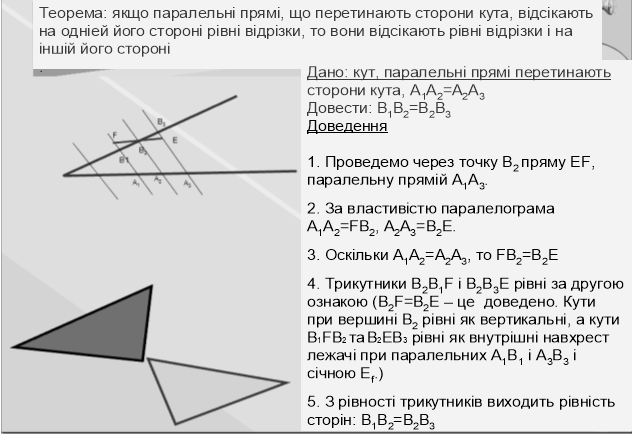
Фалес довів теорему: “Якщо паралельні прямі, що пересікають сторони кута, відсікають на одного його стороні рівні відрізки, то вони відсікають рівні відрізки і на іншій його стороні”.

При активній участі учнів розбирається доведення теореми з послідовним показом на екрані кожного етапу побудови креслення і доведення теореми.

З умови теореми Фалеса робиться висновок, що замість сторін кута можна узяти будь-які дві прямі.

 

V. Практична робота.

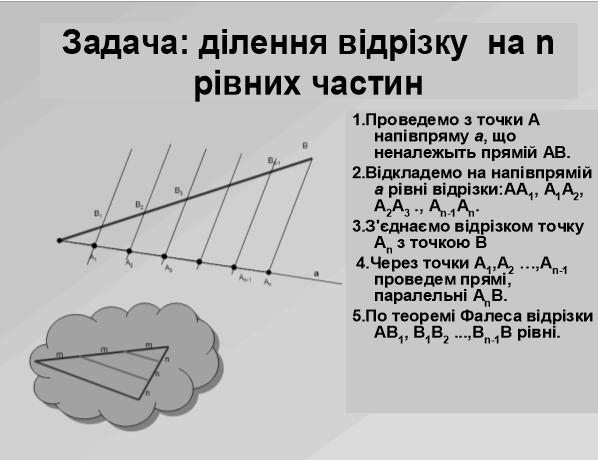
1.Учні виконують завдання на ділення відрізку довжиною в 7см. на 6 рівних частин.

Всі етапи рішення задачі учні бачать на екрані. Це сприяє зоровому запам'ятовуванню алгоритму рішення даної задачі.

 

2. Розглядається розв’язок задачі за допомогою програми GeoGebra. Учні разом з вчителем на комп'ютерах ділять відрізок на три рівні частини.

Використовуються ІНСТРУМЕНТИ GeoGebra:

• стрілка;

• лінійка (відрізок, промінь).

 

Використовуються КОМАНДИ GeoGebra:

• побудови;

• правка;

 

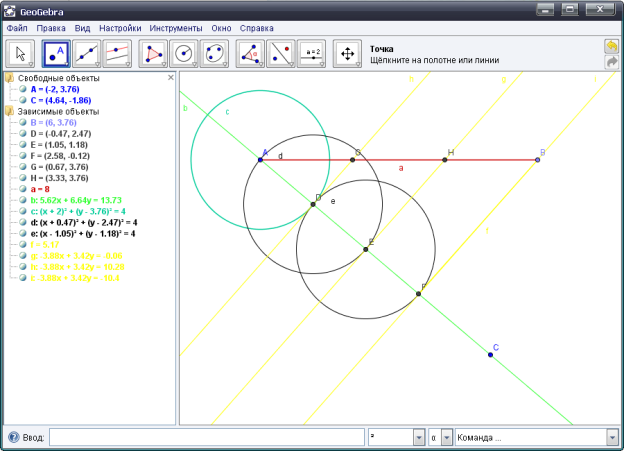
Порядок роботи:

1 . Побудуємо даний відрізок АВ.

2. Проведемо з т. А напівпряму а, що не належіть прямій АВ.

3. Відкладемо на напівпрямій а 3 рівних відрізка.

Для цього використовуємо команду ПОСТРОЄНІЯ— “коло по центру і радіусу”; задамо довільний радіус 2 і побудуємо на напівпрямій а три кола.

Вони відсікають на напівпрямій а рівні відрізки АD=DЕ=EF.

4.З'єднаємо крапки В і F.

5. Проведемо через точки D і E прямі, паралельні прямій В F.

6. Вони перетинають відрізок АВ в точках G і Н, які ділять відрізок АВ на 3 рівних частини; за теоремою Фалеса:

Якщо паралельні прямі, що перетинають сторони кута, відсікають на однієй його стороні рівні відрізки, то вони відсікають рівні відрізки і на іншій його стороні.

 

VІ. Заключна частина

Домашнє завдання.

 

Завдання: Розділити відрізок завдовжки 5 см. на 7 рівних частин. Вивчити теорему Фалеса.

Підведення підсумків уроку.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК