Розробка уроку на тему "Ламана і многокутник"
Тема. Ламана і многокутник
Мета: сформувати в учнів поняття:
- ламана та її елементи;
- проста ламана;
- многокутник та його елементи;
- периметр многокутника;
- опуклий многокутник;
- внутрішній та зовнішній кути многокутника;
- многокутник, вписаний у коло та многокутник, описаний навколо кола.
Формувати вміння відтворювати означення вивчених понять; на готовому рисунку знаходити зображення вивчених понять, і навпаки, виконувати рисунок із зображенням вивчених понять за умовою задачі; застосовувати зміст вивчених понять під час розв'язування найпростіших задач.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Ламана. Многокутник».
Хід уроку
І. Організаційний етап
Оскільки урок є першим у третьому розділі курсу геометрії для 8 класу («Многокутники. Площі многокутників»), то на цьому етапі уроку доречно буде надати учням інформацію про:
- орієнтовний план вивчення третього розділу;
- кількість навчальних годин;
- приблизний зміст матеріалу;
- основні вимоги до знань та вмінь учнів;
- приблизний зміст завдань, що будуть винесені на контроль.
(Цю інформацію можна помістити на стенді «Довідково-інформаційний куточок» у кабінеті математики та з метою економії часу запропонувати учням для самостійного ознайомлення у позаурочний час.)
II. Перевірка домашнього завдання
Якщо на попередньому уроці було задано виконати письмове завдання (аналіз розв'язання задач контрольної роботи, корекційну роботу тощо), то правильність виконання цієї роботи вчитель перевіряє, зібравши зошити учнів на перевірку (для оцінювання).
III. Формулювання мети і завдань уроку
Для свідомого розуміння учнями логіки вивчення навчального матеріалу та з метою сприяння кращому засвоєнню змісту матеріалу вчитель пропонує учням розв'язати просте логічне завдання:
Порівняйте об'єкти, зображені на рис. 1. Що спільного мають ці об'єкти? Чим вони відрізняються? Який із цих об'єктів ви б видалили як зайвий? Чому?
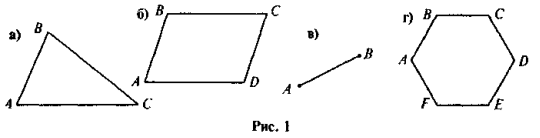
Розв'язання завдання допомагає учням повторити та систематизувати знання щодо виду геометричних фігур, властивості яких учні вивчали у 7-8 класах, а також усвідомити необхідність узагальнення цих знань (поняттям многокутника). Отже, формулюється мета уроку: узагальнити знання учнів про зміст загального поняття многокутника, окремими випадками якого є трикутник та чотирикутник, а також вивчити питання про застосування деяких властивостей вивченого поняття.
IV. Актуалізація опорних знань
 З метою успішного засвоєння учнями змісту понять уроку учням слід активізувати знання і вміння щодо означення та елементів трикутника й чотирикутника; змісту поняття «опуклий чотирикутник»; «внутрішній та зовнішній кути трикутника та чотирикутника»; поняття чотирикутника, вписаного в коло, та чотирикутника, описаного навколо кола; поняття периметра трикутника та чотирикутника; означення та властивості суміжних кутів.
З метою успішного засвоєння учнями змісту понять уроку учням слід активізувати знання і вміння щодо означення та елементів трикутника й чотирикутника; змісту поняття «опуклий чотирикутник»; «внутрішній та зовнішній кути трикутника та чотирикутника»; поняття чотирикутника, вписаного в коло, та чотирикутника, описаного навколо кола; поняття периметра трикутника та чотирикутника; означення та властивості суміжних кутів.
Виконання усних вправ
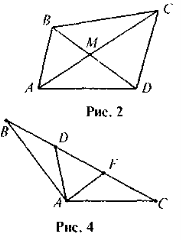
- Знайдіть усі трикутники, дві вершини яких знаходяться в точках А та В (рис. 2).
- Чи є на рисунку 3 суміжні кути; вертикальні кути? Відповідь поясніть.

-
Назвіть кути, кожний з яких є зовнішнім для кількох трикутників,
зображених на рис. 4. - Чотирикутники, як відомо, бувають опуклі й неопуклі. А чому про трикутники не говорять, що вони не бувають опуклі чи неопуклі?
- Чому дорівнює сума всіх кутів опуклого чотирикутника?
V. Засвоєння знань
План вивчення нового матеріалу
- Поняття ламаної; елементи ламаної.
- Проста ламана.
- Многокутник; елементи многокутника. Внутрішня область многокутника.
- Периметр многокутника.
- * Кількість діагоналей многокутника.
- Опуклі многокутники.
- Куги многокутника. Правильний многокутник.
- Многокутник, вписаний у коло; многокутник, описаний навколо кола.
Матеріал §15 нового підручника є досить традиційним, однак, порівняно з відповідним змістом попередніх підручників, він містить деякі нові елементи. Згідно з новою програмою з математики для дванадцятирічної школи разом із поняттям многокутника визначається і поняття многокутника, вписаного в коло, і многокутника, описаного навколо кола; формулюється поняття внутрішньої області многокутника. Проте деякі поняття, що традиційно вивчатись у цій гемі, в новому підручнику відсутні: відсутня теорема про властивість довжини ламаної, як і саме поняття довжини ламаної (хоча її наслідок про довжину сторони многокутника подано в підручнику як опорна задача); також вилучено поняття плаского многокутника . Якщо рівень пізнавальної активності учнів досить високий, то до матеріалу, який міститься в підручнику, автор пропонує додати ще формулу для обчислення кількості діагоналей п-кутника та поняття правильного многокутника, тим самим даючи можливість розширити діапазон задач на застосування теореми про суму кутів опуклого многокутника.
Оскільки п. 15.1 підручника містить досить багато нової термінології (у попередні роки на вивчення цього матеріалу відводилось 2 уроки), на ньому уроці теорему про суму кутів опуклого чотирикутника краще не вивчати (щоб не переобтяжувати учнів новим матеріалом), проте, залежно від рівня інтелектуальної активності учнів, учитель може прийняти рішення про інший розподіл навчального часу: на цьому уроці вивчити зміст теоретичних понять та виконати роботу на закріплення знань учнів, а наступного уроку — відпрацьовувати вміння застосовувати вивчений матеріал під час розв'язування задач.
Вивчення нового матеріалу п. 15.1 підручника вчитель на свій розсуд або проводить сам, використовуючи рис. 136, 137, 138, 139 підручника (або конспект 16). або організує самостійну роботу учнів з оволодіння знаннями за поданим планом. Правильність розуміння учнями змісту вивчених понять закріплюється під час розв'язування відповідних усних вправ (див. нижче) після вивчення кожного поняття або після вивчення змісту всього теоретичного матеріалу уроку.
|
|
Конспект 16 |
|
|
Ламана. Многокутник |
||
|
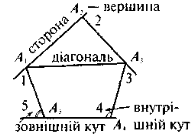
Ламана Означення. Фігура, яка складається з точок А1, А2, ..., Ап, послідовно сполучених відрізками, називається ламаною. Ламана А1А2А3А4Ап: точки А1, А2, А3.... — вершини ламаної; А1 і Ап — кінні ламаної; відрізки А1А2, А2А3.... — ланки ламаної. |
|
|
|
Проста ламана Немає самоперетинів |
Замкнена ламана Кінні збігаються |
|
|
|
|
|
|
Многокутник |
||
|
Означення. Замкнена проста ламана, сусідні ланки якої не лежать на одній прямій, називається многокутником. |
||
|
|
|
|
|
Многокутник А1А2А3...Ап називається п -кутником, у нього точки А1, А2, А3, ... — вершини; відрізки А1А2, А2А3,... — сторони; сума сторін: Р = А1А2 + А2А3 + ... — периметр; відрізки, що з'єднують несусідні вершини: А1А3, A1A4, ... — діагоналі;
кути А1, А2, ... — внутрішні кути; кути |
||
|
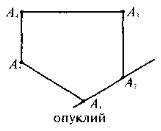
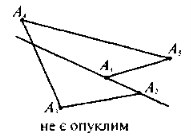
Опуклі многокутники |
||
|
|
|
|
|
Властивості (опуклих) многокутників |
||
|
В опуклому п-кутнику: 1) із кожної вершини можна провести п – 3 діагоналі;
2) кількість усіх діагоналей дорівнює 3) для будь-якої сторони а справедливо, що а < Р (Р — периметр п-кутника); 4) сума внутрішніх кутів Sп = 180°(п – 2); 5) сума зовнішніх кутів, взятих по одному при кожній вершині — 360°;
6) якщо всі сторони і всі кути рівні, то п-кутник с правильним, і тоді (Р = ап, Р — периметр; а — сторона);
|
||
VI. Формування первинних умінь
Виконання усних вправ
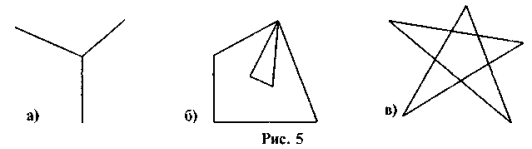
- Чи можна вважати ламаними фігури, що зображені нарис. 5? Дайте пояснення.
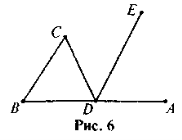
- Назвіть вершини, ланки ламаної (рис. 6). Чи є ламана простою? замкненою?
- На якому з рисунків (рис. 7) зображено опуклий многокутник?

- Скільки діагоналей виходить з однієї вершини семикутника?
- Чи може діагональ шестикутника ділити його:
а) на два трикутники;
б) на два чотирикутники;
в) на трикутник і п'ятикутник?
-
Діагональ відтинає від п'ятикутника чотирикутник. Який вид має
частина, що залишилася?
Виконання графічних вправ
Накресліть опуклий п'ятикутник.
а) Проведіть усі діагоналі п'ятикутника. Скільки діагоналей виходить з однієї вершини?
б) Яка фігура утворилася при попарному перетині діагоналей?
 в) Виміряйте кути п'ятикутника та обчисліть їх суму. Перевірте здобутий результат, користуючись відповідною теоремою.
в) Виміряйте кути п'ятикутника та обчисліть їх суму. Перевірте здобутий результат, користуючись відповідною теоремою.
Виконання письмових вправ
-
В опуклому п'ятикутнику ABCDE вершина В з'єднана рівними діагоналями з вершинами D і Е. Відомо, то
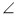 ABE =
ABE = 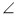 CBD,
CBD, 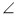 BEA =
BEA = 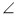 BDC. Порівняйте периметри чотирикутників ABDE і BCDE.
BDC. Порівняйте периметри чотирикутників ABDE і BCDE.
- Довжина будь-якої сторони многокутника менша від суми довжин решти сторін Доведіть.
Розв'язування як усних, так і письмових вправ спрямоване на:
- закріплення учнями ви вченої термінології (тому, виконуючи коментарі до задач, учні мають правильно відтворювати назви вивчених понять);
- формування вмінь учнів переходити від нових понять уроку до вже відомих їм та наводити доказові міркування, ґрунтуючись на здобутих раніше знаннях.
VII. Підсумки уроку
Який з об'єктів нарис. 9 зайвий? Чому?

VІІІ. Домашнє завдання
Вивчити зміст та формулювання означень нових понять. Розв'язати задачі
- Накресліть опуклий шестикутник.
а) Проведіть червоним кольором діагональ, яка ділить даний шестикутник на два чотирикутники. Скільки існує таких діагоналей?
б) Проведіть синім кольором діагональ, яка ділить даний шестикутник на трикутник і п'ятикутник. Встановіть закономірність між кількістю кутів опуклого многокутника і сумарною кількістю кутів многокутників, на які він ділиться діагоналлю.
- Периметр опуклого многокутника дорівнює 20 см Чи може його діагональ дорівнювати 10 см? Відповідь поясніть.
-
У шестикутнику ABCDEF усі сторони рівні. Більша діагональ, проведена з вершини А, паралельна стороні ВС,
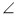 BAD =
BAD = 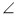 CDA. Порівняйте периметри п'ятикутників ACDEF і ABDEF.
CDA. Порівняйте периметри п'ятикутників ACDEF і ABDEF.


про публікацію авторської розробки
Додати розробку