Сума кутів опуклого многокутника

Тема. Сума кутів опуклого многокутника

Мета: закріпити знання змісту понять, вивчених на попередньому уроці. Працювати над засвоєнням учнями змісту та доведення теореми про суму кутів опуклою многокутника.

Сформувати вміння:

• відтворювати зміст вивченої теореми;
• застосовувати теорему під час розв'язування задач на знаходжен­ня градусної міри кутів многокутників.

Тип уроку: засвоєння нових знань, умінь та навичок.

Наочність та обладнання: конспект «Ламана. Многокутник».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Математичний диктант

1. Закінчіть речення:

Ламаною називається фігура, яка складається з ...

2. Дано незамкнену просту ламану ABCDE. Виконайте її зображен­ня. Назвіть усі вершини та ланки ламаної.
3. Закінчіть речення:

Многокутником називається...

4. В опуклому многокутнику ABCDE назвіть: сторони; вершини; діа­гоналі, проведені з точки В. Виконайте зображення цього много­кутника та, провівши необхідні вимірювання, обчисліть периметр многокутника.
5. Скільки всього діагоналей можна провести в опуклому п'ятикутнику?
6. Дано коло (О; R). Як виконати зображення деякого шестикутника, вписаного в це коло?

III. Формулювання мети і завдань уроку

Учням пропонується до уваги логічна вправа (рис. 1). Яке число пропущене?

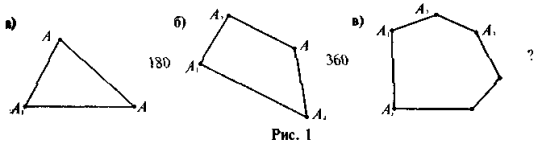
Легко помітивши закономірності записів у першому та другому рядках (рис. 1), учні усвідомлюють, що для виконання завдання слід найти суму кутів опуклого многокутника. Під час обговорення мож­ливих варіантів відповідей слід спрямувати думки учнів у такому на­прямку: сума кутів многокутника не є сталим числом, у разі збільшення кількості сторін (кут)в) сума збільшується. Отже, слід з'ясувати, чи існує залежність суми кутів многокутника S_п від кількості сторін п, і якщо існує, то як цю залежність задати аналітично. Пошук відповіді на це запитання є метою уроку.

IV. Актуалізація опорних знань

З метою успішного засвоєння учнями змісту теореми про суму кутів опуклого многокутника та ідеї її доведення слід активізувати знання і вміння щодо застосування теореми про суму кутів трикутника; зна­чення повного центрального кута, означення многокутника, означен­ня зовнішнього кута многокутника, означення правильного многокут­ника.

Виконання усних вправ

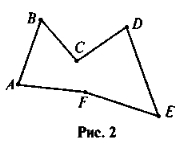
1. Чи можна провести діагоналі у шестикутнику (рис. 2)? Якщо можна, то скільки?
2. Чи можна побудувати чотирикутник із двома прямими і двома тупими кута­ми?
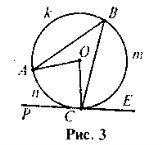3. Чи може найменший кут чотирикутника дорівнювати 92°?
4. Чи може у трикутнику один із кутів бути більшим за суму двох ін­ших? Чи може один з кутів опуклого чотирикутника бути більшим за суму трьох інших його кутів?
5. Скільки діагоналей можна провести з од­нієї вершини опуклого п-кутника?
6. О — центр кола (рис. 3). РЕ ОС, АkВ : ВтС : АпС = 3 : 4 : 2. Знайдіть: АkВ, ACP, ВСЕ.

V. Засвоєння знань

План вивчення нового матеріалу

1. Теорема про суму кутів опуклого многокут­ника.
2. Сума зовнішніх кутів многокутника.

3*. Внутрішній та зовнішній кут правильного многокутника.

 Теорема про суму внутрішніх кутів опуклого многокутника тради­ційно вивчається в темі «Многокутники» як основна властивість кутів многокутника. Але доведення цієї теореми, запропоноване авторами нового підручника, суттєво відрізняється від традиційно­го способом утворення трикутників, через обчислення суми кутів яких визначається сума внутрішніх кутів многокутника (див. рис. 740 підручника).Тому для кращого розуміння учнями доведення теореми слід обговорити з учнями такі питання.

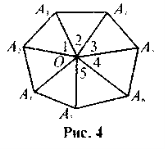
• У внутрішній області многокутника позначено довільну точку, з якої проведено відріз­ки до вершин трикутника. На які фігури роз­бивається даний многокутник? Скільки таких фігур утворилося? (Після цього виконується зображення многокутника як на рис.4 під­ручника з додатковими позначеннями, рис. 4). 
• Чому дорівнює сума кутів кожного три­кутника нарис. 4? Чому дорівнює сума всіх кутів трикутників при вер­шині О? Чи є кути 1, 2, ... трикутників при вершині О кутами много­кутника? Чи буде сума кутів усіх трикутників на рис. 4 дорівнювати сумі кутів даного многокутника? На яку величину сума кутів трикутників буде більшою за суму кутів многокутника?

Після такого ретельного обговорення доведення теореми про суму кутів опуклого многокутника не має викликати в учнів труднощів (єди­ний спірний момент — обґрунтування того, що сума кутів трикутників при вершині О дорівнює 360º, вирішується посиланням на властивість вимірювання повного центрального кута).

Оскільки з теореми про суму кутів опуклою многокутника безпо­середньо випливає низка цікавих фактів, то після доведення теореми та первинного її закріплення (на усних вправах) учні вивчають питан­ня про суму зовнішніх кутів опуклого многокутника, взятих по одному при кожній вершині; про внутрішній кут правильного многокутника; про зовнішній кут правильного многокутника. Здобуті співвідношен­ня мають бути зафіксовані в зошитах (див. конспект 16) в алгебраїчній формі (у вигляді формул). Перед початком розв'язування геометрич­них задач слід нагадати учням про технологію роботи із формулами та поновити відповідні вміння.

VI. Формування первинних умінь

Виконання усних вправ

1. За формулою S_n = 180°(п – 2) знайдіть значення:

а) S_n, якщо п = 4, п = 5, п = 6;

б) п, якщо S_n = 180°, S_n = 1800°, S_n = 900°.

За формулою знайдіть значення:

а) α, якщо п = 4, п = 5, п = 6;

б) п, якщо α = 108°.

2. Знайдіть суму внутрішніх кутів:

а) 6-кутника; б) 10-кутника; в) 102-кутника.

3. Знайдіть внутрішній кут правильного:

а) 5-кутника; б) 10-кутника; в) 18-кутника.

4. Чи може опуклий п'ятикутник мати чотири гострі кути; чотири прямі кути; чотири тупі кути?
5. Чи можуть чотири куги опуклого п'ятикутника дорівнювати від­повідно чотирьом кутам опуклого чотирикутника?

Зауваження. Перед виконанням завдання 5 доцільно обговорити питання: на скільки градусів, збільшиться сума кутів опуклого много­кутника, якщо кількість його кутів (сторін) збільшити на: 1; 2; т?

Виконання письмових вправ

1. Знайдіть суму кутів опуклого:

а) шестикутника; б) дванадцятикутника.

2. Визначте кількість сторін опуклого многокутника, сума кутів яко­го дорівнює:

а) 540°;    б) 900°;    в) 1260°.

3. Два кути опуклого п'ятикутника прямі, а решта три рівні. Знайдіть їх градусну міру.
4. Визначте, чи існує опуклий многокутник, сума кутів якого дорів­нює:

а) 1620°; б) 1350°; в) 1980°.

У випадку ствердної відповіді вкажіть кількість його сторін.

5. Діагональ ділить опуклий многокутник на п'ятикутник і чотири­кутник. Визначте вид даного многокутника і знайдіть суму його кутів.
6. Визначте кількість сторін опуклого многокутника, кожен кут якого дорівнює:

а) 60°; б) 108°; в) 120°.

7. Скільки сторін має правильний многокутник, якщо кожний із зов­нішніх його кутів дорівнює:

а) 36°; б) 24°; в) аº?

8*. П'ять кутів многокутника дорівнюють по 138°, а всі інші — по 150°. Скільки діагоналей можна провести в цьому многокутнику?

9*. В опуклому многокутнику є 5 кутів з градусною мірою 140° кожний, усі інші кути — гострі. Знайдіть кількість сторін цього многокутника.

VII. Підсумки уроку

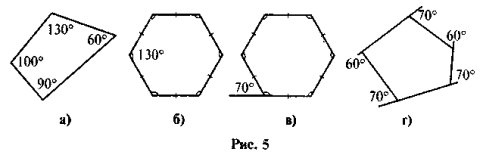
Знайдіть помилки в зображенні опуклих многокутників (рис. 5). Відповідь обґрунтуйте.

VIII. Домашнє завдання

Вивчити теоретичний матеріал, що розглядався на уроці.

Розв'язати задачі.

1. Усі кути опуклого восьмикутника рівні. Знайдіть їх градусну міру.
2. П'ять кутів опуклого шестикутника дорівнюють 120°. Доведіть, що в цьому шестикутнику всі кути рівні.
3. Три кути опуклого многокутника дорівнюють 80°, а решта — по 160°. Визначте кількість сторін многокутника.
4. Усі кути опуклого многокутника прямі. Доведіть, що він є прямокутником. Повторити: одиниці вимірювання площ, формули площі прямокутника і квадрата.

Розв'язати задачу на повторення.

Обчисліть площу заштрихованої фігу­ри (рис. 6). Скількома способами це можна зробити?