Розв'язування задач на рух, суміш

Розв’язування задач на рух, суміші Підготувала вчитель математики Городянської гімназіїСтефурак Галина Василівна. Алгебра

Повторимо ! Алгоритм розв’язування задач1) вибирають деяку невідому величину і позначають її буквою (наприклад, x)2) інші невідомі величини (якщо вони є) виражають через введену букву; 3) за умовою задачі встановлюють відношення між невідомими та відомими значеннями величин і складають рівняння;5) знаходять значення невідомого, а якщо треба за умовою задачі, то й значення інших невідомих величин; 4) розв’язують складене рівняння;6) відповідають на запитання задачі.

Запишіть вираз, за допомогою якого можна знайти відстань, яку долає велосипедист за 3 години, рухаючись зі швидкістю v км/год1.2.3.4. S = 𝟑𝒗 S = 𝒗𝟑 S = 3 vv = 3 S

Запишіть вираз, за допомогою якого можна знайти час, за який долає велосипедист S , рухаючись зі швидкістю 15 км/год3.2.1.4. S = 15tt = 𝟏𝟓𝑺 t = 𝑺𝟏𝟓 t = 15 S

Запишіть вираз, за допомогою якого можна знайти швидкість, яку розвиває автомобіль, долаючи 120 км за t год1.2.3.4.v = 120t v = 𝒕𝟏𝟐𝟎 v = 𝟏𝟐𝟎𝒕 t = 120 v

Треба запам’ятати!- швидкість руху v; - час руху t; - відстань або шлях S;S= v∙t; v = 𝑺𝒕;  t = 𝑺𝒗  

Задачі на рух дуже зручно і швидко розв’язувати за допомогою рівнянь, методом складання таблиці та поступовим її заповненням. {3 C2 FFA5 D-87 B4-456 A-9821-1 D502468 CF0 F}t (год)S (км) 1-й вид руху2-й вид руху

Задача на рух. Задача 1. Відстань між двома містами мотоцикліст проїхав за 0,8 год, а велосипедист – за 4 год. Швидкість велосипедиста на 48 км/год менша від швидкості мотоцикліста. Знайдіть швидкість кожного з них. Розв’язання:{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}V, км/год(швидкість)t,год(час)S, км(відстань) Мотоцикліст. Велосипедист Маємо рівняння:4х = 0,8(х + 48);4х = 0,8х + 38,4;3,2х = 38,4;х = 38,4 ÷ 3,2;х = 12. Отже, швидкість велосипедиста дорівнює 12 км/год, а швидкість мотоцикліста дорівнює 12 + 48 = 60 км/год. Відповідь: 12 км/год, 60 км/год.хх+4840,84х0,8(х+48)

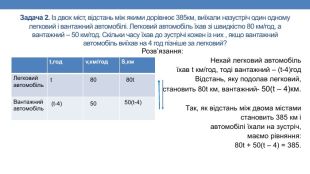
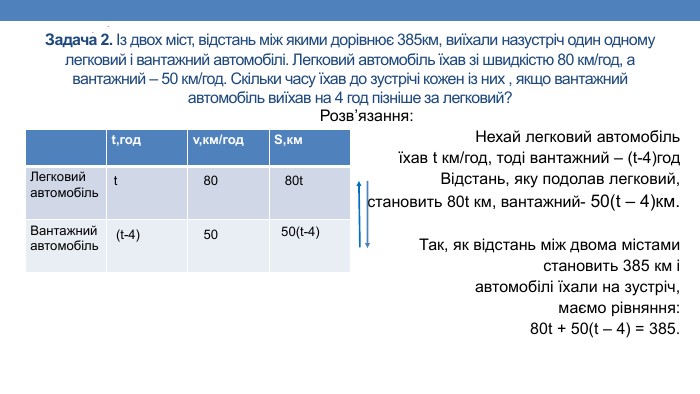
Задача 2. Із двох міст, відстань між якими дорівнює 385км, виїхали назустріч один одному легковий і вантажний автомобілі. Легковий автомобіль їхав зі швидкістю 80 км/год, а вантажний – 50 км/год. Скільки часу їхав до зустрічі кожен із них , якщо вантажний автомобіль виїхав на 4 год пізніше за легковий?Розв’язання: Нехай легковий автомобіль їхав t км/год, тоді вантажний – (t-4)год. Відстань, яку подолав легковий, становить 80t км, вантажний- 50(t – 4)км. Так, як відстань між двома містамистановить 385 км і автомобілі їхали на зустріч, маємо рівняння: 80t + 50(t – 4) = 385.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}t,годv,км/год. S,км. Легковийавтомобіль. Вантажнийавтомобільt(t-4)805080t50(t-4)

Розв’язання:80t + 50(t – 4) = 385.80t+ 50t – 200 = 385;130t = 385 + 200;130t = 585;t = 585 ÷130;t = 4,5. Отже, легковий автомобіль їхав 4,5 год, а вантажний 4,5 – 4 = 0,5 год. Відповідь: 4,5 год; 0,5 год. 

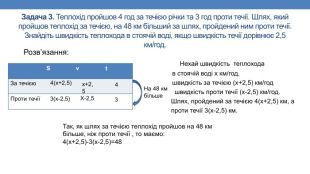
Задача 3. Теплохід пройшов 4 год за течією річки та 3 год проти течії. Шлях, який пройшов теплохід за течією, на 48 км більший за шлях, пройдений ним проти течії. Знайдіть швидкість теплохода в стоячій воді, якщо швидкість течії дорівнює 2,5 км/год. Розв’язання: Нехай швидкість теплохода в стоячій воді х км/год, швидкість за течією (х+2,5) км/год швидкість проти течії (х-2,5) км/год. Шлях, пройдений за течією 4(х+2,5) км, а проти течії 3(х-2,5) км. {B301 B821-A1 FF-4177-AEE7-76 D212191 A09}Svt. За течією. Проти течіїНа 48 км більше Так, як шлях за течією теплохід пройшов на 48 км більше, ніж проти течії , то маємо:4(х+2,5)-3(х-2,5)=484(x+2,5)3(x-2,5)x+2,5 X-2,543

Розв’яжемо рівняння:4(х+2,5)-3(х-2,5) = 48;4х+10-3х+7,5 = 48;х = 48–17,5;х = 30,5. Швидкість теплохода в стоячій воді дорівнює 30,5 км/год. Відповідь: 30,5 км/год.

Задача 4. Відстань між двома містами річкою на 55 км менша, ніж по шосе. З одного міста до другого можна дістатися теплоходом за 6 год, а по шосе автобусом – за 3 год 30 хв. Знайдіть швидкості автобуса й теплохода, якщо швидкість теплохода на 30 км/год менша від швидкості автобуса. Розв’язання: Нехай швидкість теплохода дорівнює х км/год. 3 год 30 хв = 33060=312=3,5год Так, як відстань річкою менша, ніж по шосе на 55 км, маємо рівняння: 3,5(х+30) - 6х=55; {B301 B821-A1 FF-4177-AEE7-76 D212191 A09}v, км/годt,год. S,км. Теплохід. Автобусx. X-3063,56x3,5(x+30)

Розв’язання:3,5(х+30)-6х=55;3,5х+105-6х=55;-2,5х=55-105;-2,5х=-50;х=20. Отже, швидкість теплохода становить 20 км/год, тоді швидкість автобуса дорівнює 20 + 30 = 50 км/год. Відповідь: 20 км/год, 50 км/год.

Задача 5. Сплав міді зі сріблом містить 40% міді, причому у сплаві срібла на 200 г більше, ніж міді. Знайдіть масу сплаву. Розв’язання Нехай загальна маса сплаву х г, тоді міді в ньому 0,4 х, а срібла в сплаві х - 0,4х = 0,6х г. Оскільки срібла на 200 г більше, ніж міді, то маємо рівняння:0,6х-0,4х = 2000,2х = 200х = 1000(г)Відповідь: 1000г=1 кг.

Приклад 6. До 120г розчину, 80% солі, додали 480 г розчину, 20% солі. Скільки відсотків солі вийшло в розчині? Розв’язання {B301 B821-A1 FF-4177-AEE7-76 D212191 A09}Маса розчину, г% вмістсоліМаса солі , г. Розчин ІРозчин ІІРозчин ІІІ{B301 B821-A1 FF-4177-AEE7-76 D212191 A09}Маса розчину, г. Маса солі , г. Розчин ІРозчин ІІРозчин ІІІНехай вийшло в розчині х % солі. Маємо рівняння:600х=192;х=192÷600;х=0,32;0,32∙100=32%Відповідь: 32%. 1204806008020x120*0,8=96480∙0,2=96 600x

Задача 7. Маємо два сплави міді та цинку. Перший сплав містить 9 % цинку, а другий – 30 %. Скільки кілограмів кожного сплаву треба взяти, щоб отримати зливок сплаву масою 300 кг, який містить 23 % цинку? Розв’язання:{B301 B821-A1 FF-4177-AEE7-76 D212191 A09}Маса сплаву,г% вмісту мідіМаса міді, г. Сплав ІСплав ІІСплав ІІІ{B301 B821-A1 FF-4177-AEE7-76 D212191 A09}Маса сплаву,г. Маса міді, г. Сплав ІСплав ІІСплав ІІІНехай маса І сплаву х г, тоді ІІ сплаву – (300-х) г. Маємо рівняння:х300-х3009%=0,09 30%=0,3 23%=0,23 0,09х0,3(300-х)0,23∙300 

Розв’язання:0,09х + 0,3(300-х) = 0,23∙300;0,09х + 90 - 0,3х = 69;0,09х – 0,3х = 69 – 90;-0,21х = -21;х = -21÷−0,21;х = 100. Отже І сплаву треба взяти 100г, а ІІ сплаву треба взяти 300г -100г=200г Відповідь: 100г, 200г. 

До наступної зустрічі!

Список використаних джерел {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Підручник. Видавництво. Автор. Сторінки. Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Х.: Гімназія, 2016. А. Г. Мерзляк,В. Б. Полонський,М. С. Якір20 – 27 Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Київ: Генеза, 2015. О. С. Істер176 – 183