Розв’язування задач на застосування теореми про три перпендикуляри

НВК «Ерудит» м. Києва

 

 

 

 

 

Урок в 10 класі на тему :

Розв’язування задач на застосування

теореми про три перпендикуляри

 

 

 

 

 

 

Вчитель математики

 Манько Л.А.,

            вчитель-методист

 

 

 

 

 

 

 

 

Тема уроку: Розв’язування задач на застосування теореми про три перпендикуляри.

Мета уроку: Формувати вміння застосовувати теорему про три перпендикуляри при розв’язуванні задач на знаходження відстані від точки до прямої; використовувати властивість точки, рівновіддаленої від сторін многокутника, розвивати логічне мислення.

Не досить оволодіти премудрістю, потрібно також користуватися нею.

Цицерон

Хід уроку

І Організаційний етап, перевірка готовності учнів до уроку

ІІ Мотивація навчання, повідомлення теми, мети уроку

• Давайте пригадаємо, де застосовується теорема про три перпендикуляри.

Ваші відповіді доповнить презентація «Практичне застосування теореми про три перпендикуляри в техніці»

Питання. Як повинна бути розташована стріла МЕ підйомного крана, встановленого на триколісному візку, щоб кран не завалився?

 

 

 

 

 

 

 

 

 

 

 

 

 

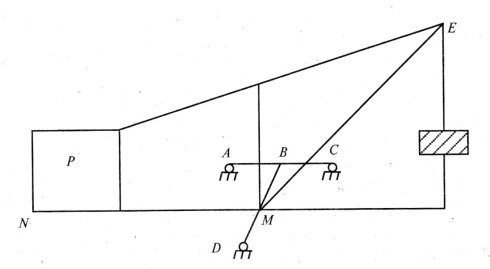
Стріла МЕ повинна бути перпендикулярною до осі ВDвізка, тому що MN – поздовжня вісь симетрії площини – перпендикулярна до осі візка.

ІІI Перевірка домашнього завдання на встановлення відповідностей з метою підготовки до ЗНО за таблицею з відповідями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№	1	2	3	4
1	В	Г	А	Б
2	Г	А	Д	В
3	В	Д	Г	А
4	Д	Г	А	Б

 

ІV Актуалізація опорних знань

Перший етап. «Теорія – основа практики»

Мета – повторити опорні знання теоретичного матеріалу, які будуть використані під час уроку.

Мозковий штурм.

1.                   Що називається відстанню від точки до прямої?
2.                   Де розміщені всі точки простору рівновіддалені від сторін многокутника?
3.                   За якими формулами знаходять радіуси кола вписаного в трикутник?

Продовжіть речення

• Дві прямі перпендикулярні до однієї площини…
• В результаті паралельного проектування середина відрізка зображується…
• В результаті паралельного проектування паралельні відрізки зображуються…
• Точка перетину бісектрис трикутника є центром …
• h = за цією формулою можна обчислити…
• Діагоналі ромба перетинаються під…
• Площа довільного трикутника за трьома сторонами знаходиться за формулою…
• Пряма проведена на площині перпендикулярно до проекції похилої…

V Застосування знань, умінь і навичок.

Другий етап «Практика – велика сила»

Усне розв’язування задач із використанням готових рисунків

1. 

 
 

 

 

 

 

 

 

 

 

 

 

 

VІ Формування вмінь, відпрацювання навичок

Письмова вправа (колективно)

Точка S, яка лежить поза площиною даного прямого кута, віддалена від вершини кута на 10 см, а від його сторін на - 8 см. Знайдіть відстань від точки S до площини кута.

Відповідь: 2√7 см.

VII Проводимо гру «Лабіринт» з метою, щоб учні перевірили свої вміння та навички в розв’язуванні задач.

Учні об’єднуються в групи по 4 чоловіка. Кожній групі роздаємо по 2 задачі з однаковими умовами. Представник від кожної групи вибирає свій лабіринт задачі (свій варіант числових даних)

Під час розв’язування у учнів є вибір працювати самостійно чи скористатись допомогою керівника групи.

Двоє учнів демонструють виготовлені ними моделі до цих задач(випереджувальне завдання). Потім вивішуємо таблицю з відповідями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Варіант	Задача 3		Задача 4
	r=ON	KN	OK	SK
1	3	5	2,4	3
2	1,5	2,5	12	20
3	2	4	4,8	6
4	8	10	12	13
5	√2	3	24	26
6	4	5	7,2	9

 

 

 

 

 

 

 

 

 

 

Індивідуальна робота

Задача 1

Через вершину В квадрата АВСD проведено перпендикуляр BN до площини АВС. Чи буде пряма NA перпендикулярною до  сторони AD квадрата?

А) так; Б) ні; (Змоделюй за допомогою стереометричного набору)

Задача 2

З вершини С гострого кута ромба (кут С дорівнює 60⁰) проведено перпендикуляр СМ до площини ромба. Побудуйте відстань від точки М до прямої AD.

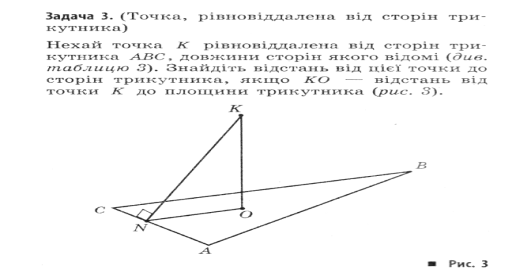
Задача 3

Точка М розміщується на середині бічної сторони рівнобічної трапеції ABCD. З даної точки до площини трапеції проведено перпендикуляр МК завдовжки 8 см. Визначте відстань від точки К до діагоналі АС, якщо АВ = ВС = 24 см, кут АВС дорівнює 120⁰.

VIII Завдання додому на вибір: (за окремими тестами)

ІХ Підіб’ємо підсумок уроку за допомогою двох дієслів – «знаю» та «вмію». (Відповіді учнів.)

Як ви розумієте девіз уроку?

Наш урок підтвердив, що ви вмієте застосовувати набуті знання на практиці.

Дякую за співпрацю на уроці!