Презентація. Екстремуми функції
Про матеріал
Ця презентація може бути корисною для пояснення нової теми вчителем на уроці, а також для самостійного опрацювання нового матеріалу учнями в умовах дистанційного навчання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

![ТЕМА. Тема. Екстремуми функціїВиконаємо разом (на повторення)1) f(x)= 2х3+6х2+3;D(f)=R;f’(x)= 0;f’(x)= 6х2+12х;6х2+12х =0;6х(x+2)=0;х=0, x=-2 – критичні точки;+–-20х+Функція зростає на проміжку хϵ(-;-2]U[0;+)Функція спадає на проміжку хϵ[-2;0] ТЕМА. Тема. Екстремуми функціїВиконаємо разом (на повторення)1) f(x)= 2х3+6х2+3;D(f)=R;f’(x)= 0;f’(x)= 6х2+12х;6х2+12х =0;6х(x+2)=0;х=0, x=-2 – критичні точки;+–-20х+Функція зростає на проміжку хϵ(-;-2]U[0;+)Функція спадає на проміжку хϵ[-2;0]](/uploads/files/878068/169237/181853_images/1.jpg)

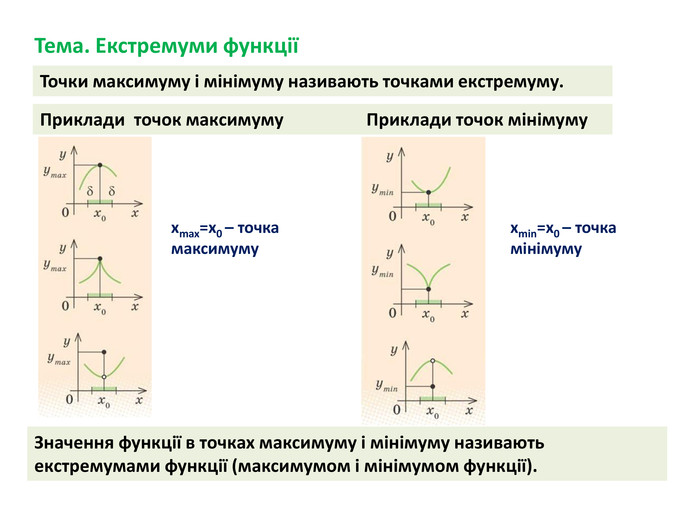
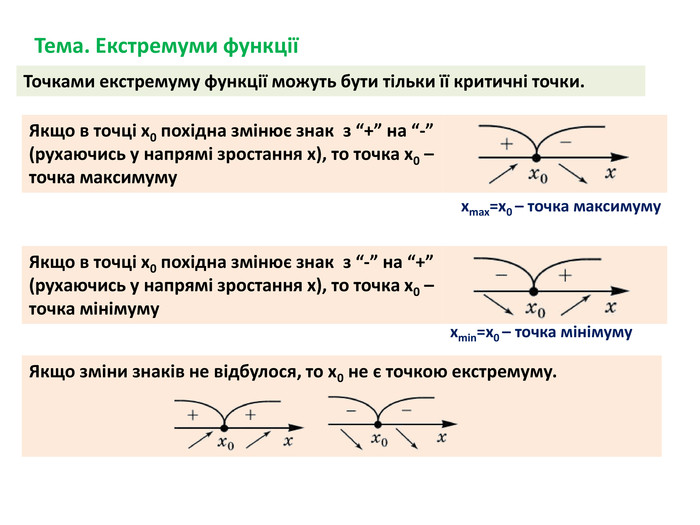

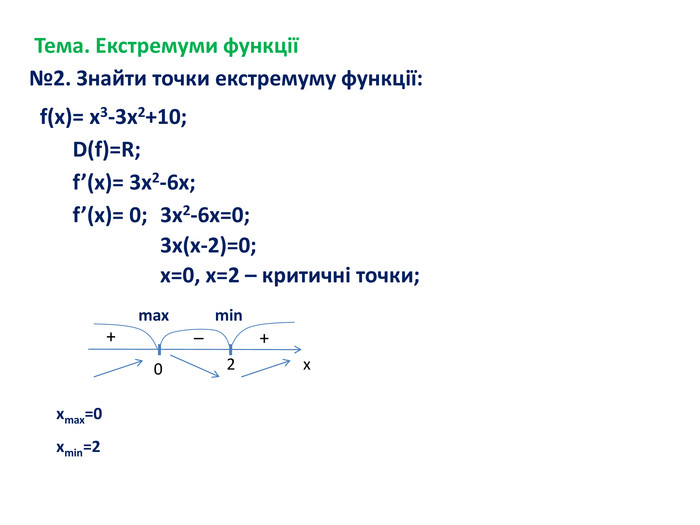
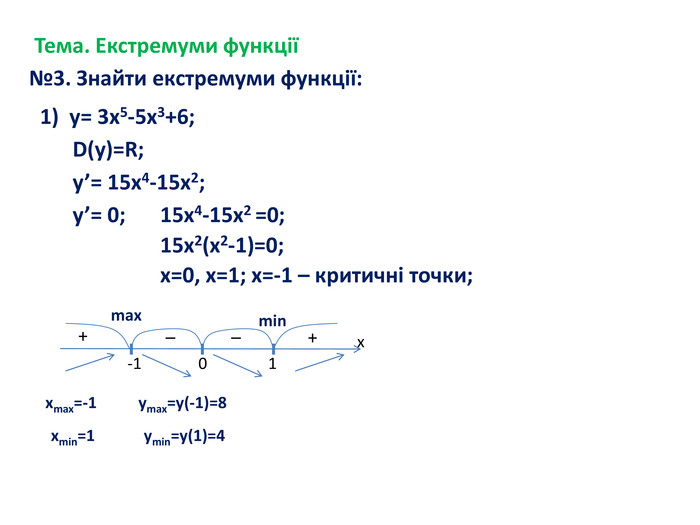




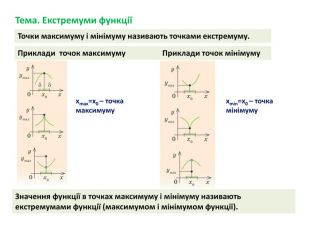
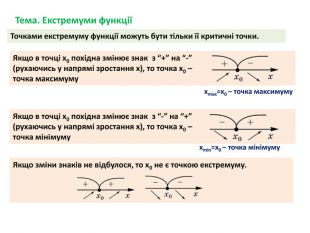


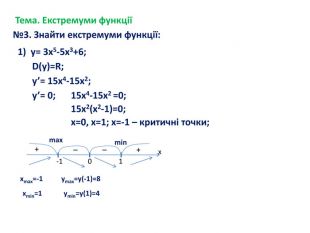


-

Литвиненко Анна Миколаївна
02.03.2025 в 16:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мельник Сергій Олексійович
08.12.2022 в 16:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
09.11.2022 в 09:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shaga Tanya
06.05.2022 в 11:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
10.04.2022 в 21:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Базиляк Наталія
07.04.2021 в 21:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Губа Тетяна
03.04.2021 в 09:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Циганок Лариса Анатоліївна
31.03.2021 в 10:15
Дуже сподобалась презентація. Дякую!!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 5 відгуків