Розв'язування задач про середні лінії трикутника та трапеції

Тема. Розв'язування задач про середні лінії трикутника та трапеції

Мета: закріпити знання учнів щодо змісту та способів доведення теореми Фалеса, властивості середньої лінії трикутника та середньої лінії трапеції, а також опорних фактів, що випливають з цих твер­джень; відпрацювати вміння застосовувати вивчені твердження під час розв'язування задач; провести проміжну діагностику засвоєння знань та вмінь із теми.

Тип уроку: комбінований.

Наочність та обладнання: конспект № 6-8.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Правильність розв'язання домашніх письмових завдань перевіря­ється під час обговорення за рисунками та записами, виконаними за­здалегідь на дошці (записи виконує або вчитель, або сильні учні).

III. Формулювання мети і завдань уроку

З метою створення позитивної мотивації навчальної діяльності учнів на уроці пропонуємо розглянути рисунок 1 та дати відповіді на запитання.

Запитання та завдання

1. Які відомі вам геометричні фігури ви бачите на рис. 1?
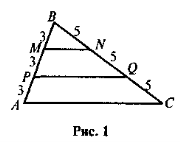2. Чи можна сказати, що відрізки MN і PQ є середніми лініями трикутника ABC?
3. Назвіть на рис. 1 фігуру, для якої відрі­зок MN є стороною. Назвіть фігуру, для якої відрізок MN є середньою лінією; запишіть рівність, що виражає влас­тивість середньої лінії з названої фігури для відрізка MN.
4. Назвіть фігуру, для якої відрізок PQ є стороною. Назвіть фігуру, для якої відрізок PQ є середньою лінією; запишіть відповідну рівність для відрізка PQ.
5. Порівняйте відповіді на запитання, зробіть висновок.

Виконання запропонованого завдання допоможе учням усвідо­мити, що в задачах, де мова йде про поділ сторін трикутника (чотири­кутника) паралельними прямими на рівні відрізки можливе застосу­вання властивостей середньої лінії як трикутника, так і трапеції, причому один і той самий відрізок може відігравати роль як основи, так і середньої лінії.

Тому неабияке значення має питання про формування вмінь виді­ляти в таких задачах вивчені об'єкти (середні лінії трикутників та тра­пецій) і про відпрацювання вмінь застосовувати вивчені властивості середніх ліній у взаємозв'язку, обумовленому умовою задачі. Ця теза виражає основну мету уроку.

IV. Актуалізація опорних знань

Щоб підготуватися до оволодіння вміннями взаємозв'язаного ви­користання властивостей середніх ліній трикутника та трапеції, учням слід активізувати знання і вміння щодо змісту теореми Фалеса, озна­чення та властивостей середньої лінії трикутника та середньої лінії трапеції.

Цю роботу можна провести в такій формі: до уваги учнів пропо­нується серія рисунків (рис. 2), за якими вони мають скласти якомога більше правильних тверджень, що мають відношення до теми.

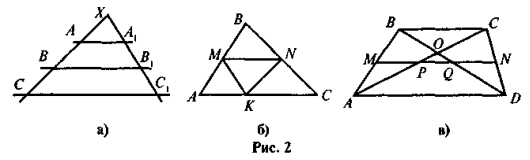
V. Застосування знань

Задача 1. Через точки, які ділять бічну сторону трапеції на три рівні частини, проведено прямі, паралельні основам трапеції. Знайдіть дов­жини цих прямих, що містяться всередині трапеції, якщо її основи дорівнюють 2 м і 5 м.

Розбираємо розв'язання задачі за підручником, складаємо план розв'язання. Складений план є орієнтовною схемою дій під час розв'я­зування аналогічних задач.

Задача 2. Сторону АВ трикутника ABC поділено на три рівних части­ни. Через точки поділу проведено прямі, паралельні стороні ВС. Наймен­ший з утворених відрізків дорівнює 3 см. Знайдіть довжину сторони ВС.

Розв'язуємо задачу 2, узагальнюємо спосіб її розв'язання. Порів­нюємо складені схеми та узагальнюємо їх.

VI. Засвоєння вмінь та навичок

Виконання письмових вправ

1. Сторона АВ трикутника ABC дорівнює 12 см. Сторону ВС поділено на 3 рівні частини і через точки поділу проведено прямі, паралельні стороні АВ. Знайдіть довжини відрізків прямих, які містяться між сторонами трикутника.
2. Бічну сторону трапеції поділено на 6 рівних частин. Через точки поділу проведено прямі, паралельні основам. Перший і останній із відрізків цих прямих, обмежений бічними сторонами трапеції, відповідно дорівнюють 4 см і 8 см. Знайдіть основи трапеції.
3. Пряма, яка паралельна основі рівнобедреного трикутника і прохо­дить через середину бічної сторони, відтинає від даного трикутника трапецію. Знайдіть її периметр, якщо периметр даного трикутника дорівнює 26 см, а основа відноситься до бічної сторони як 5:4.
4. Як побудувати трикутник, якщо задано середини його сторін?

VII. Підсумки уроку

Самостійна робота

Варіант 1

1. На рис. 1 АА₁ || ВВ₁ || СС₁, АС = 8 см. Знайдіть х, у і z.
2. На рис. 2  АС || KL || MN. Знайдіть х і у.

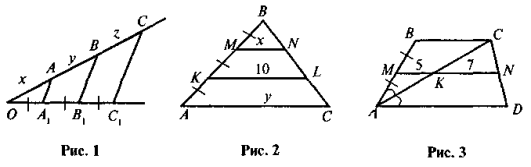
3. На рис. 3 ABCD — трапеція. Знайдіть P_ABCD.

Варіант 2

1. На рис. 1 АА₁ || ВВ₁ || СС₁, ОВ₁ = 12 см. Знайдіть х, у.
2. На рис. 2  АС || KL || MN. Знайдіть х, у.

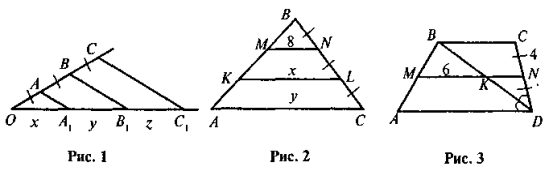
3. На рис. 3 ABCD — трапеція. Знайдіть Р_ABCD.

VIII. Домашнє завдання

Повторити зміст теоретичного матеріалу.

Виконати домашню самостійну роботу.

1. Два кути трапеції дорівнюють 120° і 80°. Знайдіть невідомі кути трапеції.
2. Знайдіть середню лінію рівностороннього трикутника з перимет­ром 54 см.
3. Діагоналі трапеції ділять її середню лінію на три рівні частини. Знай­діть меншу основу трапеції, якщо більша основа дорівнює 48 см.
4. Бічна сторона трапеції дорівнює меншій основі. Доведіть, що діаго­наль трапеції лежить на бісектрисі її гострого кута.