Розв’язування задач з кінематики ч. II

 

Тема.          Розв’язування задач.

Мета.         Продовжувати формувати вміння розв’язувати задачі з кінемати-

тики, розвивати логічне мислення, самостійність; домагатися високої                  культури зображення малюнків; виховувати колективізм, взаємовиручку;  продовжувати розвивати інтерес до фізики.

Тип уроку. Узагальнення і систематизація набутих знань.  

 

Хід уроку

 

І. Актуалізація опорних знань

Сьогодні ми з вами продовжуємо працювати над вивченням розділу механіки – кінематика.

Вашим домашнім завданням було повторити теоритичний матеріал та скласти задачі з даної теми.

(За бажанням декілька учнів біля дошки пропонують свої варіанти задач та їх розв’язання. Останні учні здають на перевірку вчителеві виготвлені на картках завдання з розв’язанням).

ІІ. Об’явлення теми та очікуваних результатів

Тема нашого уроку – “Розв’язування задач”. Ми продовжуємо готуватися до тематичної контрольної роботи. В кінці уроку ми з’ясуємо, хто допущений до тематичної контрольної роботи; який рівень завдань буде виконувати під час написання тематичної контрольної роботи.

ІІІ. Основний матеріал

1. Теоритичний мінідопуск до атестаціі:

• кінематика – це ...
• механічний рух – це ...
• поступальний рух – це ...
• матеріальна точка – це...
• траєкторія – це ...
• шлях – це...
• переміщення – це...
• скалярна величина – це...
• векторна величина – це...
• рівномірний рух – це...
• система відліку включає в себе ...
• швидкість при рівномірному русі ...
• основна задача механіки ...

           (Теоритичний мінімум можна проводити письмово для учнів усього класу, а також за допомогою учнів-консультантів, які приймуть залік у своїх товаришів в усній формі. Консультантами можна призначати учнів, які приймали участь та набрали найвищу кількість балів у грі на попередньому уроці. Учням, які не отримали допуску до тематичної атестації, надається змога отримати його в позаурочний час).

2. Розв’язування задач.

Учні розділені по парах, за рівнем засвоєння вивченого матеріалу. Рівень засвоєння матеріалу визначається за атестаційною карткою кожного учня.

На протязі всієї роботи вчитель допомагає, перевіряє роботу кожної пари.

1. Рівень А

Учні працюють за принципом “Подивися зразок, а потім розв’язуй сам”.

Задача №1

Катер рухається проти течії річки. Знайдіть швидкість катера відносно берега, якщо його швидкість відносно води 10,5 м/с, а швидкість течії річки 0,5 м/с:

Дано:

=10,5 м/с             =  10,5м/с – 0,5м/с = 10м/с         

=0,5 м/с

 

   -?

Відповідь. Швидкість катера відносно берега 10м/с.

Знайдіть швидкість катера відносно берега, якщо він рухається за течією.

Задача №2

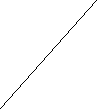
За графіком визначте швидкість тіла в кінці п’ятої секунди. Запишіть рівняння залежності x(t).                                                   х,м

 

                                                                                      5

                   Розв’язання                                               4

За графіком знайдемо координату тіла                    3

в кінці п’ятої секунди: х = 5м,                                   2

початкову координату тіла х₀ = 0.                            1

                                                                                                                               t,с

                                                                                               1   2  3  4  5

Дано:

x₀ = 0                                                                       = 1м/с     

x = 5 м              S = x – x₀

t = 5 c               

                          x = x₀ + S 

  -?                  S = t

                          x = x₀ + t;

                          x₀ = 0;       = 1 м/с

                           x = 1t

 

 

За графіком визначте швидкість тіла в кінці 3 секунди. Запишіть рівняння руху  х(t).

                                                                 х,м

                                                      8

                                                      7

                                                      6

                                                      5

                                                      4

                                                      3

                                                      2

                                                      1

                                                    

 

                                                               1   2  3  4   5          t,с     

 

Задача №3

Як повинні рухатися два автомобілі, щоб перебувати один відносно одного у спокої, а відносно інших тіл рухатися?

2 Рівень  В,С

Задача №1

Весляр спрямовує човен поперек річки, а течія відносить його так, що він рухається під кутом  до берега. Швидкість човна відносно води = 2м/с. Швидкість течії = 1,5м/с, ширина річки d = 400м. Записати рівняння руху та рівняння траєкторії човна в системі координат, пов’язаній з берегом. Знайти рівняння руху та рівняння траєкторії човна в системі координат, пов’язаній з берегом. Знайти час, за який човен перетне річку. Знайти значення і напрям швидкості човна відносно берега.

Дано:              y,м

= 2 м/с

= 1,5 м/с     400    

d = 400 м                                                

 

x(t)-?;   y(t)-?     200                                           d

y(x)-?;  -?                                   течія

        -?                                                                 х, м

1. Будемо розв’язувати задачу в системі координат ХУ,      пов’язаній з берегом, початок координат якої збігається з початковим положенням човна. Переміщення човна, що перепливає річку, відносно берега складається з переміщень S₁ – човна відносно води із швидкістю 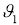       =2м/с і переміщення S₂ води у річці відносно берега води із швидкістю 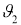=1,5м/с.  S₁ = у, S₂ = х:

 

 

x = t                               х = 1,5t          

                       або

y = t                               y = 2t

 

Виразимо час руху з першого рівняння і підставимо в друге. Дістанемо рівняння траєкторії: y = f(x) 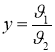         х,   або 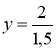х            х.

2. Час, за який човен перетне річку не залежить від швидкості течії. Він залежить тільки від швидкості човна відносно води ;  t = 200c.

3. Знайти вектор швидкості – це означає визначити його модуль і напрям. Оскільки швидкість   човна відносно води і швидкість течії   напрямлені під кутом 90, то       (за теоремою Піфагора)

                  =√ (2м/с)²  + (1,5м/с)²    = 2,5м/с

Напрям вектора   знаходимо із співвідношення:

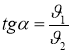,      - кут між напрямком течії

і вектором

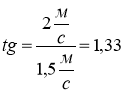;     = 53

                                                    Задача №2

Під час руху трамваю в дощову погоду зі швидкістю = 18км/год смуги від крапель дощу у його вікні вертикальні. Під час зупинки трамваю краплі дощу залишають на вікні сміги під кутом =30 до вертикалі. Визначити швидкість вітру і швидкість краплин у безвітряну погоду.

Дано:

_т = 18км/год=5м/с                           

₀ = 30                                                            

 = 0 _в

_в-? _кр -?                                                  

За умовою задачі в системі координат, пов’язаній з рухомим трамваєм, краплі рухаються вертикально вниз. Із цього можна зробити висновок, що у рухомомму трамваї не відчувається дія вітру. Повтря рухається відносно землі і є нерухомим відносно трамваю. Таким чином: _в = _т = 5м/с.

Тепер рохглянемо падяння крапель дощу за наявності вітру в системі координат, пов’язаній із нерхомим трамваєм. Краплі, що падають, беруть участь у двох рухах: рівномірному русі вниз і в рівномірному горизонтальному русі із швидкістю вітру. Тоді швидкість крапель відносно землі за наявністю вітру дорівнює векторній сумі швидкостей:   = _кр + _в.

З трикутника  знайдемо швидкість крапель:

;       ;

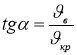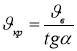= 8,6м/с

 

ІV. Підсумок (Рефлексія)

( Учитель коментує роботу учнів та оцінює їхню роботу).

 

V. Домашнє завдання.

Повторити вивчений матеріал. Виписати формули з теми.