Тема уроку. Розв’язування задач з теми “Вступ до стереометрії”.

Мета уроку: узагальнення й систематизація знань учнів. Перевірка навчальних досягнень учнів з теми “Вступ до стереометрії”.

Обладнання: стереометричний набір, моделі тетраедра і куба.

Хід уроку

І. Перевірка домашнього завдання

Перевірити правильність виконання домашньої задачі за записами, зробленими на дошці до початку уроку.

Розв’язання задачі

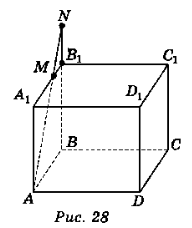
Точка N – точка перетину прямих АМ і ВВ₁ (рис. 28). ΔANB ΔMNB₁, тоді ; ; 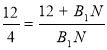12B₁N = 48 + 4B₁N; 8B₁N = 48;

B₁N = 6.

Із ΔMNB₁  MN = (cм).

Відповідь.см.

ІІ. Закріплення та осмислення знань учнів

Самостійна робота (20-25 хв)

Варіант 1

1. Прямі а і b перетинаються в точці А. Доведіть, що  пряма с,  яка перетинає дані прямі і не проходить через точку А, лежить з ними в одній площині. (4 бали)
2. Пряма АВ і точки С, D не лежать в одній площині. Доведіть, що прямі АВ і CD не перетинаються. (4 бали)
3. У Трикутній піраміді SABC побудувати переріз площиною, яка проходить через сторону АВ і точку М, яка лежить на середині ребра SC. (4 бали)

Варіант 2

1. Дано пряму а і точку А, що не лежить на цій прямій. Доведіть, що пряма с, яка проходить через точку А і перетинає пряму а, лежить з ними в одній площині. (4 бали)
2. Точки А, В і пряма CD не лежать в одній площині. Доведіть, що прямі АС і BD не перетинаються. (4 бали)
3. Побудувати переріз куба ABCDA₁В₁С₁D₁ площиною, яка проходить через вершину D₁ і діагональ АС нижньої основи. (4 бали)

Варіант З

1. Діагоналі чотирикутника ABCD перетинаються. Доведіть, що всі сторони даного чотирикутника лежать в одній площині. (4 бали)
2. Прямі AC і BD не лежать в одній площині. Доведіть, що прямі АВ і CD не лежать в одній площині. (4 бали)
3. Побудуйте переріз куба площиною, яка проходить через три точки, які лежать на трьох ребрах, що виходять із одній вершини (4 бали)

Варіант 4

1. Продовження двох протилежних сторін чотирикутника ABСD  перетинаються. Доведіть, що всі сторони даного чотирикутника лежать в одній площині. (4 бали)
2. Прямі AD і ВС не лежать в одній площині. Доведіть, що прямі АС і BD не лежать в одній площині. (4 бали)

3. Побудуйте переріз трикутної піраміди площиною, що проходить через три точки, які лежать на трьох бічних ребрах піраміди. (4 бали)

ІІІ. Узагальнення та систематизація знань учнів

Формування вмінь будувати перерізи многогранників

Виконання вправ

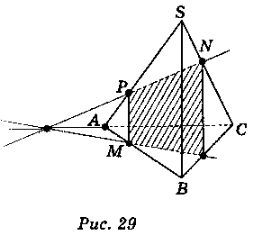
1.         У трикутній пірамід SАИС точка М – середина ребра АВ, точки Р і N лежать відповідно на ребрах SA і SC, причому АР : AS = 1 : 3, а SN  = NC. Побудувати переріз піраміди площиною, яка проходить через точки M, N, P. (Розв’язання див. на рис. 29)
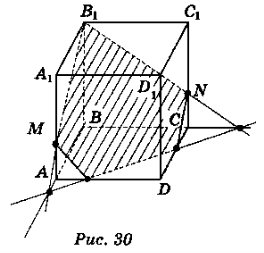2.         У кубі ABCDA₁В₁С₁D₁ побудувати переріз площиною, яка проходить через вершину В₁ і точки М на ребрі АА₁ і N на ребрі СС₁, якщо МА = 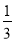АА₁, СN = 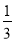СС₁. (Розв’язання див. на рис. 30)

IV. Домашнє завдання

Контрольні запитання № 1-5. Розв’язати наступну задачу.

Довжини трьох ребер прямокутного паралелепіпеда, що виходять з однієї вершини, дорівнюють 6, 6 і 8 см. Побудуйте переріз паралелепіпеда площиною, яка проходить через середини цих ребер, і знайдіть його периметр.

V. Підведення підсумків уроку

 Запитання до класу

1. Сформулюйте аксіоми стереометрії.
2. Які способи задання площини вам відомі?