Тема уроку.   Взаємне розміщення двох прямих у просторі.

Мета уроку:   вивчення взаємного розташування двох прямих у просторі: прямі, що перетинаються; паралельні прямі; мимобіжні прямі. Формування понять: паралельні прямі, мимобіжні прямі.

Обладнання: стереометричний набір, каркасна модель куба, схема “Взаємне розміщення двох прямих у просторі”.

Хід уроку

І. Перевірка домашнього завдання

Перевірку правильності виконання домашньої задачі провести шляхом фронтальної бесіди за записами, зробленими на дошці до початку уроку.

Розв'язання задачі

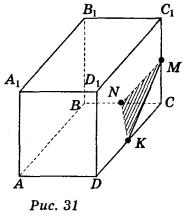ABCDA₁B₁C₁D₁ — прямокутний парале­лепіпед, у якому: AD = 6 см, DD₁ = 6 cm, DC = 8 cm (рис. 31).

СС₁ = 2MC ; DC = 2CK; BC = 2NC .

ΔΜΝΚ — шуканий переріз.

Із ΔMKC  (cм).

Із ΔNCM  (см).

Із ΔNKC  (см).

P_MNK = MN +NK+ MK = 10 + 3 (см).

Відповідь. 10 + 3 см.

Запитання до класу

1) Поясніть, що таке прямокутний паралелепіпед.

2) Як побудовано шуканий переріз?

3) Чому трикутник МСК — прямокутний?

4) Яка довжина ребра CC₁ ? Чому?

5) Яка довжина ребра ВС? Чому?

6) Визначте вид трикутника MNK.

II. Аналіз самостійної роботи, проведеної на попередньому уроці

III. Сприйняття й усвідомлення нового матеріалу

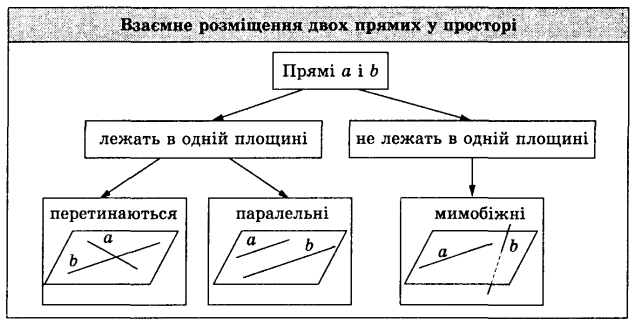
Взаємне розміщення двох прямих у просторі

Із курсу планіметрії відомо, що дві прямі, які лежать у площині, можуть перетинатися або не мати спільних точок. Якщо дві прямі ле­жать в одній площині і не мають спільних точок, то вони називаються паралельними. У просторі дві різні прямі або перетинаються, або не пе­ретинаються. Проте другий випадок допускає дві можливості: прямі ле­жать в одній площині або прямі не лежать в одній площині.

Прямі, які не перетинаються і лежать в одній площині, називають паралельними, а дві прямі, які не перетинаються і не лежать в одній площині, називають мимобіжними.

Випадки взаємного розташування двох прямих у просторі демонструються за допомогою стереометричного набору або на каркасній моделі куба.

Отже, дві прямі а і b у просторі можуть: перетинатися, бути паралель­ними, бути мимобіжними (демонструється схема, наведена нижче).

Виконання вправ

1. Різні випадки розташування двох прямих у просторі продемонст­руйте на предметах оточення.
2. Дано зображення куба ABCDA₁B₁C₁D₁ (рис. 32).

а) Чи перетинаються прямі АА₁ і ВВ₁? А₁В₁ і D₁C₁? Як назива­ються ці прямі?

б) Чи перетинаються прямі AD і ВВ₁? АВ і DD₁? Як називаються ці прямі?

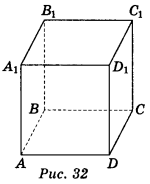в) Чи можна провести площину через пря­мі AD і DB₁? A₁D₁ і C₁D₁? AD і ВВ₁? АА₁ і DВ₁ ? АА₁ і DD₁ ?

3. Як розташовані осі залізничних вагонів між собою; відносно рейок?
4. Як треба розуміти, що прямі а і b у просто­рі не паралельні?
5. Що можна сказати про прямі а і b, якщо ві­домо, що вони не мимобіжні?

IV. Закріплення та осмислення знань учнів

Розв'язування вправ

1. Прямі АВ і CD паралельні. Чи можуть бути мимобіжними прямі АС і BD? А перетинатися?
2. Прямі АВ і CD мимобіжні. Чи можуть бути прямі АС і BD парале­льними? А перетинатися?
3. Задача № 2 із підручника (с. 18).
4. Задача № 3 із підручника (с. 18).
5. Κ, Ρ,Τ, Μ — середини ребер АВ, AC, CD, DB тетраедра DABC. Знай­діть периметр чотирикутника КРТМ, якщо AD = 6 см, ВС = 8 см.

V. Домашнє завдання

§ 1, п. 7 (до теореми 2.1); контрольні запитання № 1, 2; задача № 1 (с. 18).

VI. Підведення підсумку уроку

Запитання до класу

1) Як можуть розташовуватися дві прямі на площині?

2) Як можуть розташовуватися дві прямі у просторі?