Розв'язування задач за допомогою лінійних рівнянь

Тема. Розв'язування задач за допомогою лінійних рівнянь

Мета: систематизувати знання і вміння учнів, набутих під час вивчен­ня теми «Лінійні рівняння з однією змінною».

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

 Оскільки № 1 і 2 є завданнями такого типу, які винесені на тематич­ну контрольну роботу, перевірці саме цих завдань треба приділити більше уваги. Але водночас треба діагностувати рівень засвоєння вмінь попередніх уроків. Тому роботу на цьому етапі уроку можна організувати так:

Розв'язання № 1 та 2 біля дошки готують 4 учні; фронтально прово­диться самостійна робота*, що передбачає виконання завдань саме такого типу й рівня складності, або організовуємо роботу в групах (заздалегідь перевіривши стан виконання домашнього завдання, вибираємо учнів, які впоралися з усім домашнім завданням, і назначаємо їх консультантами в групах, при цьому групи формуємо «за інтересами», тобто за такою озна­кою: яке завдання викликало найбільші труднощі (завдання саме з № 1 та 2), така група й формується). Далі упродовж 5-7 хв учні-консультанти проводять пояснювальну роботу в групах, після чого хто-небудь з учнів кожної групи (тільки не консультант) презентує розв'язання свого завдан­ня на дошці.

(Презентація завдання означає не тільки відтворення етапів розв'язу­вання, але й відповідні коментарі, що базуються на теоретичному матеріалі.)

Самостійна робота

Розв'язання та відповіді до самостійної роботи

Варіант 1

1. ; НСК(2; 3) = 6; ;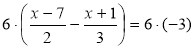

 3(х – 7) – 2(х + 1) = -18; 3х – 21 – 2х – 2 = - 18; х – 23 = -18; х = -18 + 23; х = 5. Відповідь. 5.

(х + 2) – 2х = 0,5; х + 2 – 2х = 0,5; - х + 2 = 0,5; х = 1,5.

Отже, в корзині було 1,5 кг винограду, а в ящику 2 · 1,5 = 3 (кг).

Відповідь. 1,5 кг; 3кг.

Варіант 2

1. ; НСК(4; 6) = 12; ;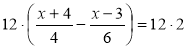

     3(х + 4) – 2(х – 3) = 24; 3х + 12 – 2х + 6 = 24; x + 18 = 24; x = 6.

Відповідь. 6.

х + 12 = 1,5(х – 3); х + 12 = 1,5х – 4,5; х – 1,5х = -4,5 – 12; -0,5х = -16,5;

х = -16,5 : (0,5); х = 33.

Отже, на другій ділянці було 33 кущі смородини, а на першій ділянці

33 + 9 = 42 кущі.

Відповідь. 42; 33 кущі.

II. Систематизація та узагальнення знань

Контрольні запитання до класу

1. Що називається коренем рівняння? Як перевіриш, чи є число коренем
   рівняння?
2. Що означає розв'язати рівняння? Скільки коренів може мати рівняння з однією змінною?
3. Які два рівняння називаються рівносильними?
4. Які властивості рівносильних рівнянь ви знаєте?
5. Яке рівняння називається лінійним рівнянням з однією змінною?
6. В якому випадку рівняння ах = b має один корінь; не має коренів? В якому випадку будь-яке число є коренем цього рівняння?
7. Які етапи в розв'язуванні задачі за допомогою лінійних рівнянь ви мо­жете виділити?

III. Застосування знань, умінь та навичок

Виконання усних вправ (завдання 1-го рівня)

1. Яке з чисел є коренем рівняння 4х + 2 = 10?
   а) 1; б) -2; в) 2; г) 3?
2. Скільки коренів має рівняння (х – 2)(х + 2) = 0?
   а) Один; б) два; в) безліч; г) не має коренів.
3. Розв'яжіть рівняння 3у + 5 = 7y – 3 та вкажіть правильну відповідь:

а) -2; б) 2; в) 0,8; г) 0,5.

4. Книжка та альбом коштують 6 грн, причому книжка в 4 рази дорожча
   від альбому. Яке з рівнянь треба скласти, щоб знайти ціну альбому (х —
   ціна альбому в гривнях)?

а) х + 6х = 4; б) 6х – х = 4; в) х + 4х = 6; г) 4х – х = 6.

 Розв'язання усних вправ можна організувати як самостійну тестову роботу.

Виконання письмових вправ

1. Чи рівносильні рівняння:  2х – 8 = 5 та х – 4 = 2,5?
2. Розв'яжіть рівняння:
   1) -0,75(2х + 5) + 0,25(х + 3) = 0,75; 2)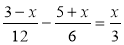 ; 3) 3|2х + 1| - 7 = 2;

4) 3 – 2(1 – 2|х|) = 11 – |х|; 5)* (|х| + 2)(|х| – 3) = 0.

3. Дано рівняння (а + 3)х = 5. При якому а:

1) коренем рівняння є число -1;

2) рівняння не має коренів;

3) коренем рівняння є будь-яке число?

4. Розв'яжіть задачу, склавши рівняння:

1) По шосе їдуть два автомобілі з однією і тією самою швидкістю. Якщо перший збільшить свою швидкість на 10 км/год, а другий зменшить на 10 км/год, то перший за 2 год проїде стільки ж, скільки другий за 3 год. З якою швидкістю їдуть автомобілі?

2) У першому бідоні в 5 разів більше молока, ніж у другому. Після того як з першого бідона перелили в другий 5 літрів, то в першому бідоні стало в 3 рази більше молока, ніжу другому. Скільки літрів молока було в кож­ному бідоні спочатку?

3)* У двох пакетах було по 11 цукерок. Після того як з першого пакета взяли в 3 рази більше цукерок, ніж з другого, в першому пакеті залиши­лося в 4 рази менше цукерок, ніж у другому. Скільки цукерок взяли з кожного пакета?

IV. Підсумок уроку

V. Домашнє завдання

1. Повторити теоретичний матеріал (див. контрольні запитання).
2. Домашня контрольна робота.

№ 1. Відшукайте корінь рівняння:

1) х = 36; 2) 12х = -6; 3) 11х – 9 = 4х + 19; 4) 7х – 5(2х + 1) = 5х+15;

5) (14х + 1)(1,8 – 0,3х) = 0.

№ 2. Розв'яжіть задачу, склавши рівняння.

В одному ящику було 200 кг апельсинів, а в другому — 120 кг. З першого ящика брали щоденно по 30 кг, а з другого — по 25 кг. Через скільки днів у першому ящику зали­шиться в 4 рази більше апельсинів, ніж у другому?

№ 3. При якому значенні b мають спільні корені рівняння 2х – 9 = 3 та

х + 3b = -10?