сума і різниця кубів
Конспект уроку з теми «Сума і різниця кубів»
Мета: Вивчити різницю і суму кубів двох виразів. Розвивати вміння застосовувати різницю і суму кубів для перетворень добутку виразів на многочлен стандартного вигляду, а також застосовувати формули суми і різниці кубів двох виразів для розкладання многочленів на множники. Самостійно застосовувати набуті знання в стандартних і нестандартних ситуаціях, а також вміти систематизувати певні математичні твердження і робити висновки.
Епіграф:
Без знання математики
неможливо зрозуміти ні
основ сучасної техніки,ні того,
як вчені вивчають природні явища.
А. М. Колмогоров.
Хід уроку:
І. Перевірка домашнього завдання.
Розкладіть на множники ( коментуємо з місця)
-
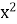 - 36
- 36
-
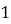 −
−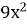
-
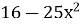
-
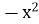 +81
+81
-
0,81-
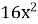
Представити у вигляді многочлена ( у дошки виконують учні)
- (а-2)2
- (х+у)2
- (4-в)2
- (m+3)2
- (5+с)2
Як називаються отримані алгебраїчні вирази? (Повний квадрат двочлена). А як ви думаєте бувають неповні квадрати двочлена.
ІІ. Організаційний момент.
Так. Давайте познайомимося з таким поняттям неповний квадрат двочлена. Замислитесь як це неповний, чого в ньому не вистачає. Вислуховую думки учнів.
Так не вистачає двійки.
Неповний квадрат виразу:
х-у ![]() -ху+
-ху+![]() Неповний квадрат різниці двох виразів
Неповний квадрат різниці двох виразів
2х+у ![]() +2ху+
+2ху+![]() Неповний квадрат суми двох виразів
Неповний квадрат суми двох виразів
5х-7у ![]() - 35ху+
- 35ху+![]() Неповний квадрат різниці двох виразів
Неповний квадрат різниці двох виразів
Самостійно знайдіть неповний квадрат виразу
6х - 5у ![]()
3х+ 8у ![]()
Давайте ще раз повторимо як це називається? Неповний квадрат різниці (суми) двох виразів. Питання а навіщо ми це вивчили? Вислуховую думки учнів. Так щоб краще зрозуміти нову тему, а саме розкладання на множники суми і різниці кубів двох виразів. А ще давайте пригадаємо і запишемо скільки буде: ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]()
ІІІ Новий матеріал
Розкладаючи на множники різницю кубів двох виразів, використовують формулу різницю кубів:
а3 ![]() b3 = (а
b3 = (а ![]() b) (а2 + аb +b2) те що я виділила як називається?
b) (а2 + аb +b2) те що я виділила як називається?
Давайте разом перевіримо правильно я розклала на множники, як це зробити? Правильно перемножити.
(а![]() b) (а2 + аb + b2 ) = а3 + а2b+ аb2
b) (а2 + аb + b2 ) = а3 + а2b+ аb2 ![]() а2b
а2b![]() аb2
аb2![]() b3 = а3
b3 = а3![]() b3.
b3.
Отже, формулу різниці кубів можна сформулювати так:
Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми.
Розкладаючи на множники суму кубів двох виразів, використовують формулу сумі кубів: а3 ![]() b3 = (а
b3 = (а ![]() b) (а2
b) (а2 ![]() аb +b2).
аb +b2).
Доведемо цю тотожність:
(а ![]() b) (а2
b) (а2 ![]() аb +b2) = а3
аb +b2) = а3 ![]() а2b+ аb2
а2b+ аb2 ![]() а2b
а2b![]() аb2
аb2![]() b3 = а3
b3 = а3![]() b3.
b3.
Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їх різниці.
ІV Закріплення
Алгебра В. Кравчук ст. 105
Розкласти на множники:
№660
а) 27а3 - 1 = (3а - 1) (9а2 ![]() 3а+ 1);
3а+ 1);
б) 1 + 64 b3 = ( 1 + 4b ) ( 1 ![]() 4b + 16b2 )
4b + 16b2 )
в) 8![]() – 27 =(2a -3)(4
– 27 =(2a -3)(4![]() +6a+9)
+6a+9)
г) 125- 27![]() = (5-3у)(25+15у+9
= (5-3у)(25+15у+9![]() )
)
№661. а) m6 ![]() n3 = (m2
n3 = (m2 ![]() n) (m4 + m2 n + n2 );
n) (m4 + m2 n + n2 );
б) а9 +b6 = (а3 + b2 ) (а6 ![]() а3 b2+ b4 );
а3 b2+ b4 );
в) а6 + с6 = (а2 + с2 ) (а4 ![]() а2 с2 + с4 ).
а2 с2 + с4 ).
№664. а) 64а3 ![]() 27b3 = (4 а
27b3 = (4 а ![]() 3b) (16 а2 + 12 а b +9 b2 );
3b) (16 а2 + 12 а b +9 b2 );
б) ![]() р3
р3 ![]() 8
8 ![]() 3 = (
3 = ( ![]() р
р ![]() 2q) (
2q) (![]() р2 +
р2 + ![]() р q + 4 q2);
р q + 4 q2);
в) 27а6 ![]() 25 = (3а2
25 = (3а2 ![]() 5) (9а4 +15а2 +25).
5) (9а4 +15а2 +25).
Щоб кожен учень міг з впевненістю сказати, що він досяг успіху, потрібно самостійно попрацювати над виконанням аналогічних завдань. Адже уміння працювати самостійно є дуже важливим етапом в навчанні і в житті. Крім того, для досягнення успіху в житті потрібно мати друзів, партнерів. То ж під час самостійної роботи дозволяється здійснювати взаємодопомогу. Вибирай сам: працювати самостійно чи за допомогою друзів.
Самостійна робота. (на картках) Підписуємо аркуші і дописуємо розв’язок.
I варіант..
- Розкласти на множники:
а) 64![]() 27у3 =
27у3 =
б) m3 ![]() 125 =
125 =
Спростити вираз:
а) (а![]() b) ( а2 + аb + b2) + b3 =
b) ( а2 + аb + b2) + b3 =
б) (х2 ![]() 1) (х4 + х2 + 1) + 1
1) (х4 + х2 + 1) + 1
II варіант.
- Розкласти на множники:
а) 1- 64b3 =
б) 27а3 ![]() =
=
Спростити вираз:
в) (а2 + b2) (а4 ![]() а2 b2 + b4)
а2 b2 + b4) ![]() а6
а6 ![]() b6 =
b6 =
г) (а +2) (а2 ![]() 2 а + 4)
2 а + 4)![]() (а
(а ![]() 2) (а2
2) (а2 ![]() 2 а + 4) =
2 а + 4) =
V Підсумок уроку.
- Повторили множення різниці двох виразів на їх суму, розкладання на множники різниці квадратів двох виразів, розкладання многочленів на множники з використанням формул квадрата суми і квадрата різниці.
- Вивчили формулу різниці кубів і суми кубів.
- Розв’язали ряд вправ на застосування формули різниці і суми кубів двох виразів.
Домашне завдання :
Повторити : п.16, 17, 18, 19. Вивчити п. 20.
Розв’язати з п.20 №659 , №662 №665 (№669)
-
Дякую


про публікацію авторської розробки
Додати розробку
