Розв'язування задач за допомогою рівнянь

Розв’язування задач за допомогою рівнянь. Підготувала вчитель математики Городянської гімназії Стефурак Галина Василівна. Алгебра

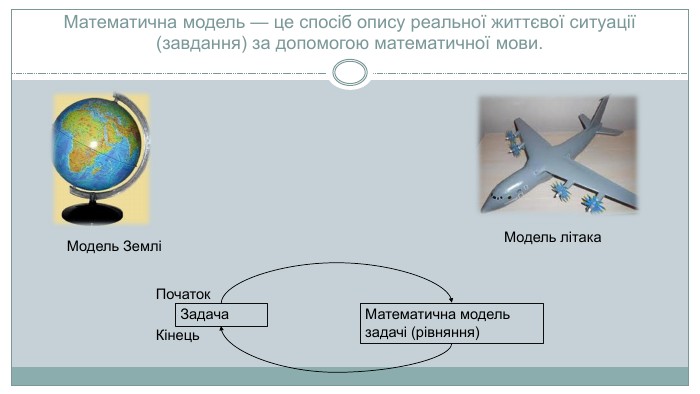
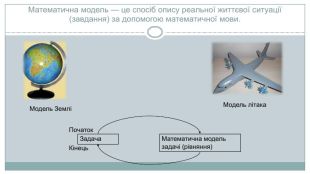
Текстова задача – це опис на звичайній мові деякої ситуації, в якій потрібно дати кількісну характеристику якої-небудь компоненти цієї ситуації, встановити відповідність певного відношення між її компонентами чи визначити вид цього відношення. Будь-яка текстова задача складається з двох частин: {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Умова- повідомляються дані про об’єкти і деякі величини, що характеризують ці об’єкти, про відомі і невідомі значення цих величин, про відношення між ними{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}- вказівка того, що потрібно знайти. Вимога. Способи розв’язування: арифметичний; алгебраїчний

Математична модель — це спосіб опису реальної життєвої ситуації (завдання) за допомогою математичної мови. Модель ЗемліМодель літака. Задача. Математична модель задачі (рівняння)Початок. Кінець

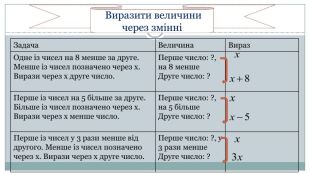
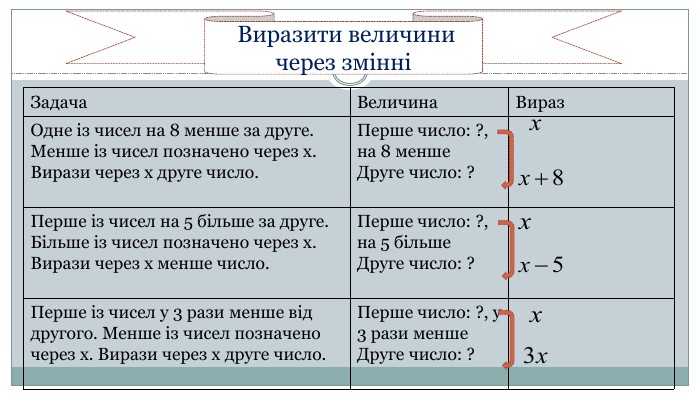
Виразити величини через змінні{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Задача. Величина. Вираз. Одне із чисел на 8 менше за друге. Менше із чисел позначено через x. Вирази через x друге число. Перше число: ?, на 8 менше. Друге число: ?Перше із чисел на 5 більше за друге. Більше із чисел позначено через x. Вирази через х менше число. Перше число: ?, на 5 більше. Друге число: ?Перше із чисел у 3 рази менше від другого. Менше із чисел позначено через x. Вирази через x друге число. Перше число: ?, у 3 рази менше. Друге число: ?

а) сума чисел 𝑥 і 20 дорівнює 25;б) сума числа 𝑥 і числа, яке на 5 більше, ніж 𝑥, дорівнює 39;в) сума числа 𝑥 і числа, яке на 16 менше, ніж 𝑥, дорівнює 23;г) сума числа 𝑥 і числа, яке втричі більше, ніж 𝑥, дорівнює 17;д) число 𝑥 на 5 більше від числа 20;х + (х+5)=39; 2) х – 20 = 5;х + 20 = 25;х + 3х = 17;5) х + (х - 16) = 23. Встановіть відповідність

Задача 1. Двоє робітників виготовили разом 127 деталей, причому перший виготовив на 13 деталей більше, ніж другий. Скільки деталей виготовив кожний робітник?1) вибирають деяку невідому величину і позначають її буквою (наприклад,х); Нехай другий робітник виготовив х деталей2) Інші невідомі величини (якщо вони є) виражають через введену букву; Тоді перший робітник виготовив (х + 13) деталей.3) За умовою задачі встановлюють відношення між невідомим та відомим значеннями величин і складають рівняння;Обидва робітники виготовили (х + х +13), що разом за умовою дорівнює 127 деталей; х + х + 13 = 127

4) розв’язують складене рівняння; х + х + 13 = 127; 2х = 114; х = 57 5) знаходять значення невідомого, а якщо треба за умовою задачі, то й значення інших невідомих величин; Отже, другий робітник виготовив 57 деталей, а перший 57 + 13 = 70.відповідають на запитання задачі. Відповідь: 70 деталей, 57 деталей. Перевірка: 70+57=127 всього деталей.

Задача 2. Три найвищі гірські вершини України – Говерла, Бребенескул і Петрос знаходяться в найвищому гірському масиві Чорногори в Карпатах. Сума їхніх висот дорівнює 6113 м, причому Говерла на 29 м вища за Бребенескул і на 41 м вища за Петрос. Знайдіть висоту кожної з вершин. Гора Бребенескул Гора Петрос. Найвища гора - х м(х – 29) м(х – 41) м

Розв’язання. Нехай висота Говерли дорівнює х м, тоді висота Бребенескула – (х-29) м, висота Петроса – (х-41)м. Оскільки сума їхніх висот дорівнює 6113 м, то складаємо рівняння:х+(х-29)+(х-41)=6113;3х-70=6113;3х=6183;х= 2061. Отже, висота Говерли дорівнює 2061 м, тоді висота Бребенескула дорівнює 2061- 29=2031 м, а висота Петроса дорівнює 2061- 41=2020м. Відповідь: 2061м, 2032м, 2020м.

Задача 3. Кілограм огірків на 0,8 грн дешевший від кілограма помідорів. Скільки коштує 1 кг помідорів, якщо за 3,2 кг помідорів заплатили стільки ж, скільки за 3,6 кг огірків?(х - 0,8) грнх грн3,2 3,6=

Розв’язання. Нехай 1кг помідорів коштує х грн, тоді 1кг огірків коштує (х-0,8) грн. Якщо за 3,2 кг помідорів заплатили стільки ж, скільки за 3,6 кг огірків, то маємо рівняння:3,6(х-0,8)=3,2х;3,6х-2,88=3,2х;3,6х-3,2х=2,88;0,4х=2,88;х=7,2. Відповідь: 7,2 грн.

Задача 4. Периметр прямокутника дорівнює 36 см, причому одна із сторін на 4 см більша за іншу. Знайдіть сторони прямокутника та його площу.х см. Р = 36 см. Р = 2(а+b) – периметр прямокутникаbа(х + 4) см. S = а ∙ b – площа прямокутника 

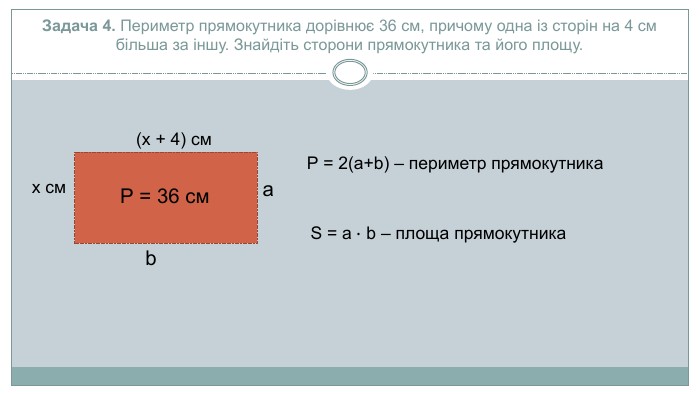
Розв’язання. Нехай одна із сторін прямокутника дорівнює х см, а інша – (х+4) см. Маємо рівняння:2(х+(х+4))=36; поділимо обидві частини рівняння на 2;х+х+4=18;2х=14;х=7. Отже одна сторона – 7см, а інша дорівнює 7 + 4 = 11 см. Площа прямокутника дорівнює 7 ∙ 11 = 77 см2. Відповідь: 7 см, 11 см, 77 см2. 

Задача 5. В одній шафі було в 4 рази менше, ніж у другій. Коли в першу шафу поклали 17 книжок, а з другої взяли 25 книжок, то в обох шафах книжок стало порівну. Скільки книжок було спочатку в кожній шафі? х4х+17-25

Розв’язання Нехай у І шафі було х книжок, тоді в ІІ – (4х) книжок. Маємо рівняння:4х-25=х+17;4х-х=17+25;3х=42;х=42:3;х=14. Отже, у І шафі було 14 книжок, а в ІІ шафі – 4∙ 14 = 56 книжок. Відповідь: 14 та 56 книжок. 

Задача 6. Вкладник поклав у банк 3000 грн на два різних депозитних рахунки, причому за першим рахунком йому нараховували 7% річних, а за другим – 8% річних. Через рік він одержав 222 грн прибутку. Яку суму було внесено на кожний рахунок? 7 %=        =0,07;          8 %=0,08;   7100  Розв’язання. Нехай підприємець поклав у банк х грн під 7% річних, тоді під 8 % річних він поклав (3000-х) грн. Маємо рівняння: 0,07х + 0,08(3000-х)=222;

0,07х + 0,08(3000-х) = 222; 0,07х + 240 – 0,08х = 222; 0,07х - 0,08х = 222 - 240; -0,01х = -18; х = 1800. Отже, підприємець поклав у банк 1800 грн під 7% річних, тоді під 8 % річних він поклав 3000 – 1800 = 1200 грн. Відповідь: 1800 грн, 1200 грн.

До якої із задач подано модель?У І бідоні  молока на 7 л менше, ніж у ІІ. Скільки літрів молока в кожному бідоні, якщо в двох бідонах разом 53 л?У І бідоні  молока на 7 л більше, ніж у ІІ. Скільки літрів молока в кожному бідоні, якщо в двох бідонах разом 53 л?У І бідоні  молока в 7 разів менше, ніж у ІІ. Скільки літрів молока в кожному бідоні, якщо в двох бідонах разом 53 л?У І бідоні  молока в 7 разів більше, ніж у ІІ. Скільки літрів молока в кожному бідоні, якщо в двох бідонах разом 53 л?АГБВ

До наступної зустрічі!

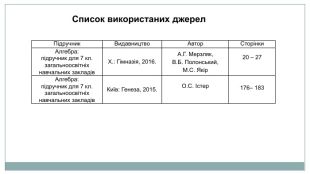
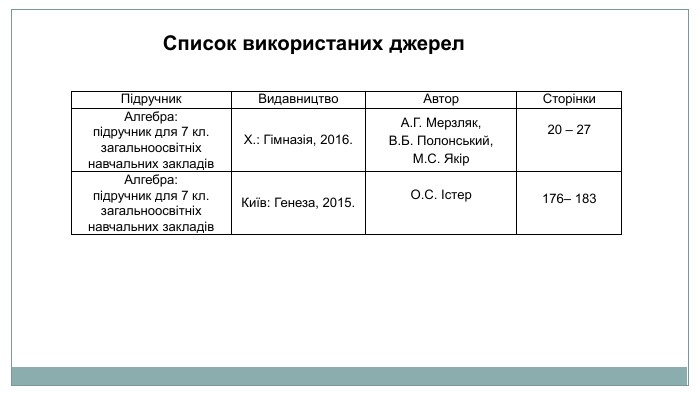
Список використаних джерел {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Підручник. Видавництво. Автор. Сторінки. Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Х.: Гімназія, 2016. А. Г. Мерзляк,В. Б. Полонський,М. С. Якір20 – 27 Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Київ: Генеза, 2015. О. С. Істер176– 183