Розвиток творчого потенціалу гуртківців засобами STEM-освіти на заняттях гуртка «Геометричне моделювання»

ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ ВИКОНКОМУ КРИВОРІЗЬКОЇ МІСЬКОЇ РАДИ

ВІДДІЛ ОСВІТИ ВИКОНКОМУ ДОВГИНЦІВСЬКОЇ РАЙОННОЇ В МІСТІ РАДИ

КОМУНАЛЬНИЙ ПОЗАШКІЛЬНИЙ НАВЧАЛЬНИЙ ЗАКЛАД

 «СТАНЦІЯ ЮНИХ ТЕХНІКІВ ДОВГИНЦІВСЬКОГО РАЙОНУ»

 КРИВОРІЗЬКОЇ МІСЬКОЇ РАДИ

 

 

 

 

 

 

 

 

 

 

 

Розвиток творчого потенціалу гуртківців засобами STEM-освіти на заняттях гуртка «Геометричне моделювання»

 

Методичний посібник

 

 Автор:

Хисна Ірина Юріївна

Керівник гуртка «Геометричне моделювання»

КПНЗ «СЮТ Довгинцівського району» КМР

 

 

м. Кривий Ріг

2021

ЗМІСТ

Вступ ………………………………………………………..…....................…..…3

1. Розвиток творчих здібностей гуртківців засобами STEM-освіти……..…….5
2.  STEM-освіта для молодших школярів………………………………….........6
3. Геометричний конструктор «ТАНГРАМ»……………………………………8
4. Конструктор з картону………………………………………………..………10
5. STEM-іграшки «Флексагони»………………………………………………..11
6. Завдання на логіку…………………………………………………………….12
7. Оригамі………………………………………………………………………...16
8. Геометричні форми………………………………………………………...…18

Висновки ...………………………………………..………………...…......……..19

Додатки………………………………………………………..………..…..…….21

Література…………………………….………………………………..……..…..68

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Сьогодення об’єктивно вимагає переведення освітнього процесу на новий технологічний рівень, активізацію пошуку перспективних інноваційних й педагогічних технологій, спрямованих на доступність якісної освіти та розвиток і саморозвиток особистості.

STEM-навчання поєднує в собі міждисциплінарний і проектний підхід, основою для якого стає інтеграція природничих наук в технології, інженерну творчість і математику. Дуже важливо навчати науці, технологіям, інженерному мистецтву і математиці інтегровано, тому що ці сфери тісно взаємопов’язані в практичній діяльності.

STEM-освіта за допомогою практичних занять демонструє дітям застосування науково-технічних знань у реальному житті.. Вони вивчають конкретний проект, в результаті чого своїми руками створюють прототип реального продукту.

STEM-освіта сприяє розвитку навичок критичного мислення та розв’язуванню проблем, необхідних для подолання труднощів, з якими діти можуть зіткнутися в житті.

STEM-заняття відрізняються активною комунікацією і командною роботою вихованців. На стадії обговорення створюється вільна атмосфера для дискусій і висловлювання думок. Вони не бояться висловити будь-яку свою думку, вчаться говорити і презентувати свої результати.

У нових умовах інформаційного суспільства STEM-підходи реалізуються у  закладах освіти України, в тому числі і в позашкіллі.

Гурткова робота – це поле для творчості та розвитку. А творчість гуртківців завжди відкриває щось нове та неординарне у звичних речах. В позашкільній освіті STEM крокує в ногу з часом та розвивається, відкриваючи нові можливості.

Варто зазначити, що заклад позашкільної освіти докладає значних зусиль щодо запровадження STEM-навчання вихованців шляхом реалізації як традиційних, так нових ефективних форм роботи з ними, які, в свою чергу, привертають увагу до STEM-професій і дають можливість для навчання за різними напрямами STEM-освіти.

Однією з форм STEM-навчання є заняття, які спрямовані на встановлення міжпредметних зв’язків і сприяють формуванню у вихованців цілісного, системного світогляду, актуалізації особистісного ставлення до питань, що розглядаються на гуртковому занятті.

Формування дослідницької компетентності у STEM-освіті потребує розвитку в гуртківців здатності до самостійних спостережень, дослідів, експериментів, що насамперед передбачає спроможність здійснювати аналіз, синтез, проводити виокремлення суттєвих ознак, робити порівняння, узагальнення та висновки.

Завдяки впровадженню елементів STEM-освіти у роботу гуртків, вихованці розвивають творчу активність, логічне мислення, технічну грамотність, вчаться вирішувати конкретні проблеми, самостійно шукати нестандартні рішення, стають новаторами і винахідниками.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. РОЗВИТОК ТВОРЧИХ ЗДІБНОСТЕЙ ГУРТКІВЦІВ ЗАСОБАМИ STEM-ОСВІТИ

Розвиток і розповсюдження інформаційно-комунікативних технологій стало глобальним викликом сучасній людині, що радикально змінює вигляд довколишнього середовища й світобачення людини. На сьогоднішній день неможливо уявити життя без мобільного телефону, комп’ютера чи Інтернету, що супроводжується новими формами комунікації і споживання.

З плином часу одні, раніше популярні професії, йдуть у вічність, інші ж, незнані і не зрозумілі, як от ІТ-програмісти, з’являються і набувають популярності на ринку праці. Така ж тенденція прослідковується і в освітніх процесах, де збільшується попит на такі предмети: ЗD-моделювання, програмування, робототехніка і багато інших інновацій. Для задоволення такого попиту необхідні нові більш складні навички. Необхідно одночасно розвивати молодь в таких напрямках, як наука, математика, технології та інженерія.

Паралельно з новітніми технологіями і наукою, важливою сферою сучасної освіти стають креативні індустрії чи галузі, що ґрунтуються на інтелектуальному і творчому капіталі.

Необхідність переходу національної освіти до методики навчання за STEM технологією полягає у потребі підготовки висококваліфікованих спеціалістів, що здатні приймати оригінальні і адекватні рішення, бачити перспективи та планувати стратегії і тактики ефективної комунікації і міжособистісної взаємодії. В таких умовах актуальності набуває питання активізації творчого потенціалу учнівської молоді, залучення її до дослідницької діяльності.

Саме в шкільному віці в учнів починають формуватись творчі здібності, необхідні для подальшого естетичного розвитку, формування духовної культури, вироблення єдності в розумінні красивого, доброго, правильного та цілісного сприйняття змісту і форми світу. Для дитини більш важливим є процес творчості, аніж її результат. Розвивати творчі здібності дитини треба з урахуванням вікових психофізіологічних особливостей, що потребує глибокого знання педагогом індивідуальних рис вихованця, уважного й тактовного ставлення до неповторності його особистості.

Тому керівникам гуртків необхідно вміти створювати сприятливі умови для навчання та творчої діяльності вихованців, що дало б їм змогу розкрити та проявити свої здібності. Адже саме творчі здібності збагачують особистість, а їх розвиток слугує підґрунтям для формування духовної культури людини.

Гурткова робота в позашкільних навчальних закладах допомагає розв’язувати питання розвитку творчого потенціалу дітей. Для реалізації передумов розвитку творчих здібностей вихованців використовуються ефективні форми й методи навчання: пояснювально-ілюстративний, розповідь, бесіди, робота з книгою, демонстрація, вправи, практичні роботи репродуктивного і творчого характеру, методи мотивації і стимулювання, навчального контролю, взаємоконтролю й самоконтролю, пізнавальна гра, проблемно-пошуковий, ситуативний, екскурсії. Потрібно проводити такі заняття, котрі можуть зацікавити гуртківців, на яких вони мають змогу фантазувати, досліджувати, спостерігати.

 

 

2. STEM-ОСВІТА ДЛЯ МОЛОДШИХ ШКОЛЯРІВ

Пошук прихованих талантів і здібностей, розвиток креативного мислення, виховання творчої особистості треба починати з наймолодшого віку. «Критичне мислення - критичне рішення» - ось принцип освіти через руки, з розумінням того, чому ти зробив те, що зробив, і чи є вплив зробленої роботи на світ. Діти мають навчитись як вчитись, вони повинні бути адаптивними, повинні сприймати і технології, і глобалізацію, ставати громадянами світу і своєї країни водночас. В зв’язку з цим необхідно звернути серйозну увагу на роботу з дітьми дошкільного і молодшого шкільного віку для забезпечення умов формування і розвитку особистості дитини, здатної успішно адаптуватися в сучасних умовах, що несе в собі SТЕМ-освіта. Процес виховання та освіти дітей повинен бути підпорядкований конкретним цілям. Найприроднішою і доступною формою досягнення поставленої мети в цьому віці є гра.

Гра, як особливий вид діяльності, являє собою процес, суть якого можна позначити як відображення і перетворення дійсності, в ході якого відбувається засвоєння суспільного досвіду, відпрацювання умінь і становлення навичок.

А. С. Макаренко писав: «Гра має важливе значення в житті дитини, має те саме значення, яке у дорослого має діяльність, робота, служба. Якою буде дитина в грі, такою вона буде і в праці, коли виросте. Тому виховання майбутнього діяча відбувається перш за все в грі».

Головну роль в становленні найменших майбутніх інженерів грає не електроніка, а творчість. В системі STEM-освіти на заняттях для дошкільників та молодших школярів на першому плані стоїть розвиток здібностей, творчого мислення і свобода створювати. Тому в роботі з такими дітьми необхідно активно використовувати прості іграшки, конструктори, кубики тощо. А найкращими формами і методами роботи з наймолодшими вихованцями є заняття з використанням ігрових технологій та STEM-іграшок.

Такі STEM-іграшки, як головоломки, сприяють розвитку нестандартного мислення. STEM-іграшки з області інженерії та конструювання не лише розвивають навички конструювання і моделювання, але й збільшують рівень комунікації між дітьми, педагогами, батьками.

Для більш простого сприйняття процесу програмування, світу електроніки та робототехніки також існують STEM-іграшки.

Отже, головоломки - таке собі «ламання» мозку - ігри на логіку. Головоломки розвивають уважність, логічне мислення, технічну кмітливість, вчать доводити розпочату справу до кінця. Систематичне використання таких ігор може змінити сприйняття дітьми навколишніх об’єктів, адже вони сприяють розвитку нестандартного мислення. Головоломки - це чудові, оригінальні і корисні ігри для занять у гуртках для молодших школярів.

 

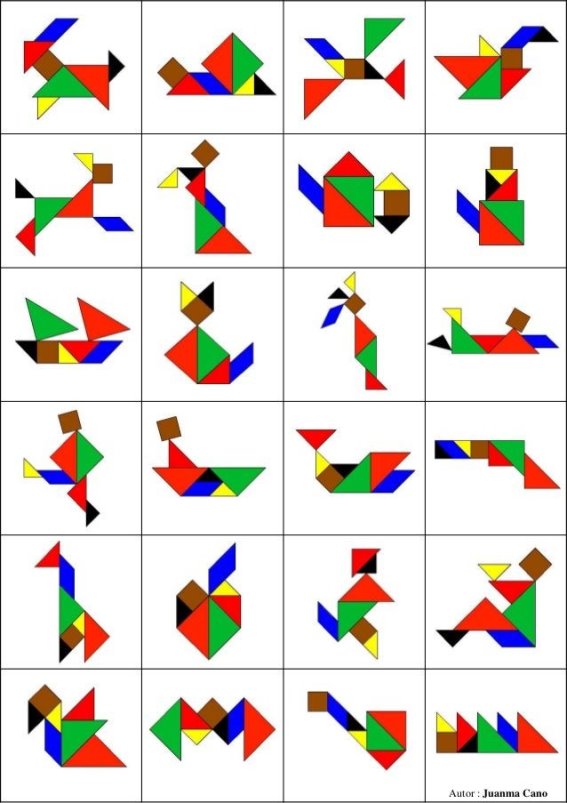
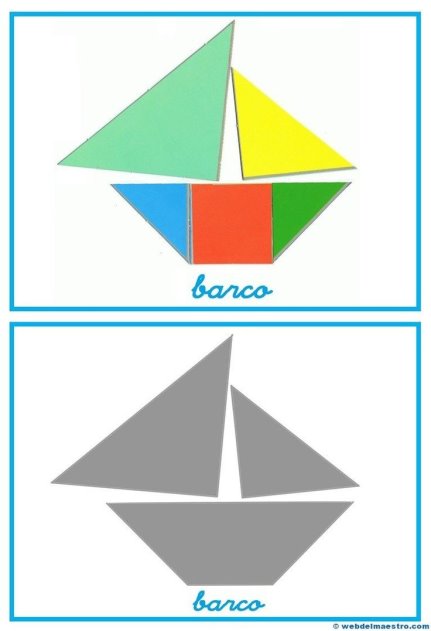
3. Геометричний конструктор «ТАНГРАМ»

Танграм часто називають головоломкою з картону або геометричним конструктором. Ця головоломка складається із семи плоских фігур, на які розрізається квадрат.

 Танграм

Малюнок 1

Складаючи певним чином дані елементи, можна утворити більш складну фігуру (людини, тварини, предмета, літери тощо). У процесі розв’язування головоломки слід дотримуватися двох правил: використовуються всі сім фігур; фігури не повинні накладатися одна на одну.

Танграм сприяє розвитку в дітей наочно-образного мислення, уяви, уваги, розуміння величини і форми, сприйняття, комбінаторних здібностей.

Розпочинаючи роботи зі складання танграму, дітям спочатку пропонується скласти фігуру за зразком, потім завдання можна ускладнити, запропонувавши відтворити фігуру за зразком-контуром.

Малюнок 2

Малюнок 3

В кінці пропонується придумати власні фігури й скласти аплікацію (Додаток А)

Виконання вищезгаданих завдань вимагає від дітей зорового розчленування форми на складові частини, тобто на геометричні фігури.

 

4. КОНСТРУКТОРИ З КАРТОНУ

Малюнок 4

Конструктори з картону – чудова заміна фабричного конструктора, який можна  виготовити власноруч. Кольорові геометричні фігури з картону допоможуть дитині розпізнавати форми, й конструювати різноманітні конструкції (Додаток Б).

Малюнок 5

5. STEM-іграшки «Флексагони»

Трикутник «жорстка» фігура. Якщо дано три його сторони, то форму його змінити не можна, не порушивши його. Ця властивість широко використовується на практиці.

Малюнок 6

У трикутника є просторові «родичі»: тетраедр, октаедр, ікосаедр. Ці геометричні тіла являються «родичами» трикутника тому, що грані цих тіл

– трикутники.

«Родичем» трикутника є й геометрична паперова стрічка, так як її поверхня складається з трикутників. Ця іграшка називається флексагон. Клаптик паперу, здатний зацікавити не тільки дитину, а й дорослих. Для деяких це не просто іграшка-головоломка, а й справжній перший крок в світ математики. Яскраві лінії складеного паперу захоплюють не гірше дитячого калейдоскопа з різнокольоровим склом. Та ще й назва така загадкова – флексагон. Що ж це таке насправді? Дуже часто тема головоломок в школі є складною і незрозумілою, але в деяких дітей це викликає неабиякий інтерес.

Флексагони – це не просто іграшка, це засіб математичного розвитку здобувачів освіти. Із року в рік STEM-іграшки набувають все більшої популярності серед дітей та їх батьків. Причини цього очевидні: бавлячись з ними, дитина водночас розвивається та навчається (Додаток Е)

 

 

 

6. ЗАВДАННЯ НА ЛОГІКУ

Головним та важливим моментом розвитку дитини є формування її логічного мислення. Завдяки логіці можна пояснити учневі життєві явища, обґрунтувати свою точку зору. Якщо вчасно розвивати вміння логічно думати і діяти, дитина обов’язково стане розсудливою людиною.

Для досягнення цієї мети вчителі та вихователі використовують різноманітні захопливі та цікаві ігри, створюють ігрові ситуації логічного характеру, що зроблять урок математики не тільки цікавим, але й будуть дуже корисним для маленьких вихованців, оскільки спрямовані на розвиток інтелекту й мислення. Такі завдання та ігри змусять маленький мозок розмірковувати, зважаючи, перш за все, на логіку.

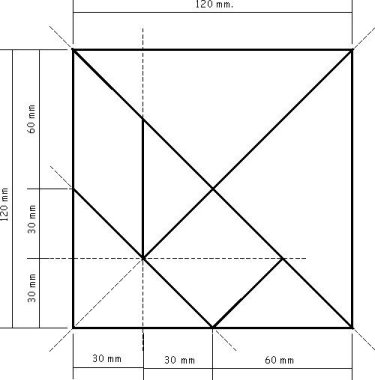
Скільки прямокутників ти бачиш на картинці?

Малюнок 7

 

Скільки квадратів ти бачиш на картинці?

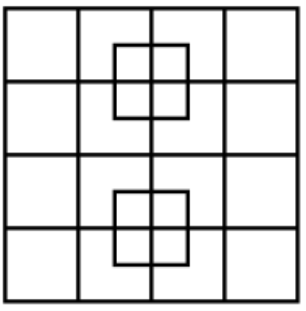
Малюнок 8

Скільки кубів зображено на малюнку?

Мова йде про фактичну кількість кубів, які необхідні для побудови фігури, що на малюнку.

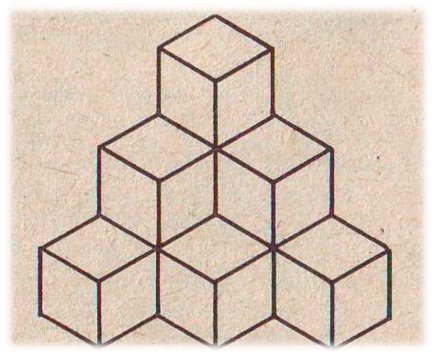
Малюнок 9

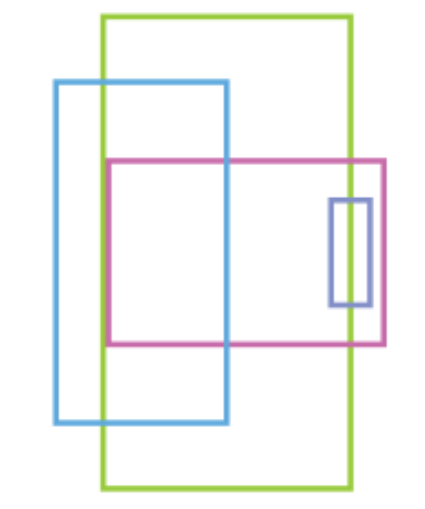
Скільки прямокутників зображено на малюнку

Малюнок 10

 Скільки трикутників є на малюнку?

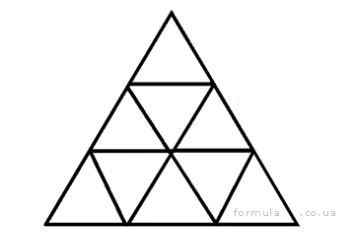
Малюнок 11

Як виглядатиме піраміда згори?

Перевірте свій інтелект. Як виглядатиме піраміда, якщо на неї дивитись згори?

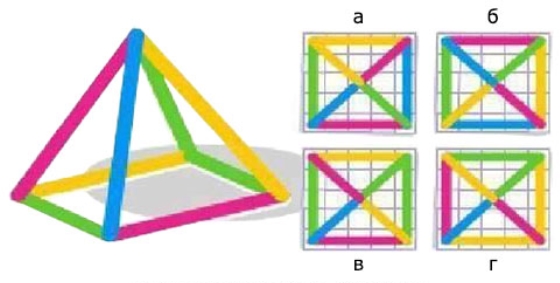Малюнок 12

Як бачить фігуру дівчинка, якщо дивиться на неї зверху? 

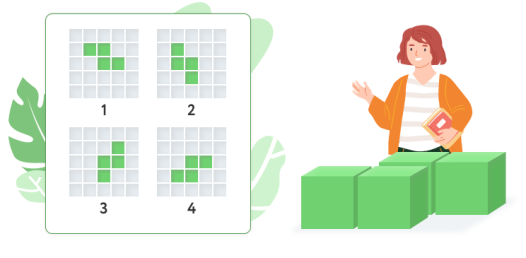
Малюнок 13

Складіть кубик-головоломку. Якого елемента не вистачає?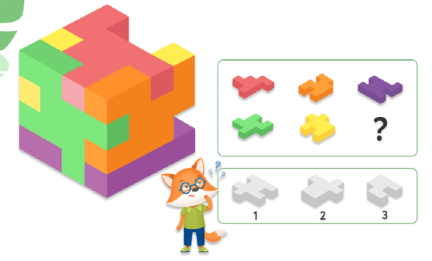

Малюнок 14

Приберіть два сірника так, щоб вийшло чотири рівні квадрати

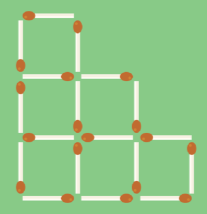
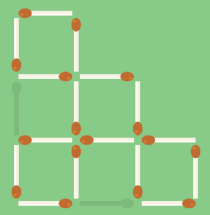
 Малюнок 15

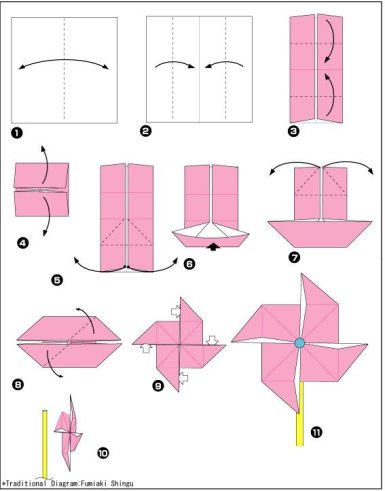
7. ОРИГАМІ

Оригамі (з японського «складання паперу») – давнє мистецтво, яке своїм корінням сягає в стародавній Китай, де і був відкритий папір. Мистецтво оригамі – інтригуюча загадка, яка манить кожну дитину неймовірними перетвореннями звичайного квадратика паперу в забавне звірятко, гарну квітку, коробочку, автомобіль або літак шляхом перегинання та складання.

Малюнок 16

 

Оригамі – це творчий процес по складанню фігурок з паперу, який розвиває конструктивне мислення, здібність комбінувати, просторове мислення, почуття форми, творчу уяву, художній смак, стимулює і розвиває пам'ять, так як дитина, щоб зробити поробку, повинна запам’ятати послідовність його виконання, прийоми і способи складання (Додаток З).

Оригамі знайомить дітей з основними геометричними поняттями: кут, сторона, квадрат, прямокутник, діагональ, трикутник, бісектриса, вісь симетрії тощо; розвиває просторову уяву, вчить читати схеми, за якими складаються фігурки, сприяє розвитку креслярських навичок (Додаток К)

Малюнок 17

 

Звертаємо увагу на завдання: знайти центр симетрії квадрата, складаючи його по діагоналі та складаючи навпіл, які дозволяють продемонструвати вихованцям утворення кута 45°, перпендикулярність прямих, визначення кількості осей симетрії квадрата та ін. Сформовані практичні навички вкрай потрібні у процесі розв’язування геометричних задач.

Малюнок 18

 

 

 

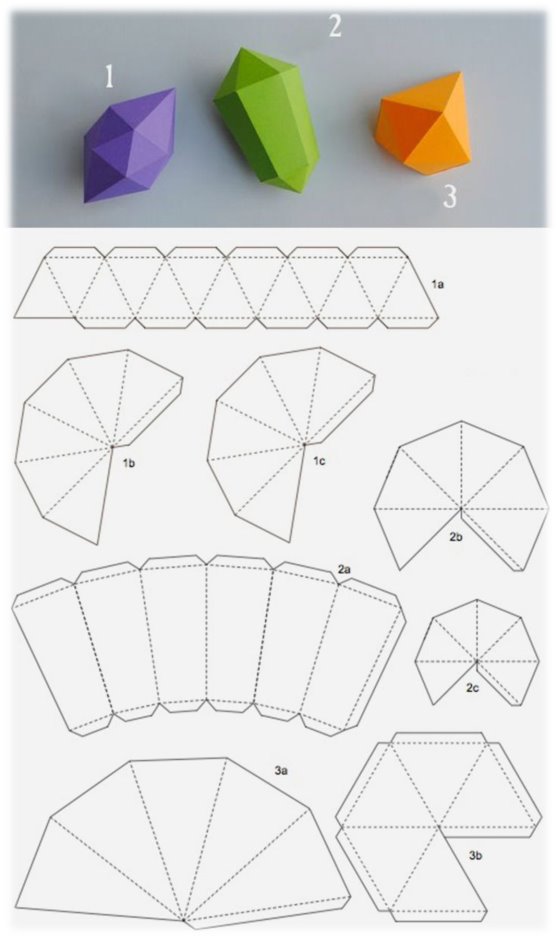
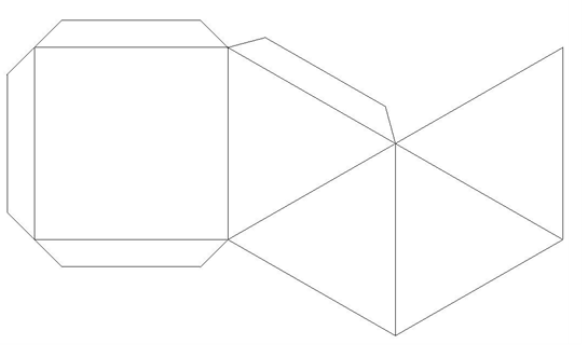
8. ГЕОМЕТРИЧНІ ФОРМИ

Форми предметів мають геометричну основу. Вони бувають простими і складними. Прості форми мають в основі будови одну геометричну фігуру, складні – кілька (Додаток О).

 

 

 

Малюнок 19

Для закріплення в свідомості учнів об’ємно-просторового уявлення про будову цих форм ефективно зробити їх своїми руками. Моделі конструюються з паперу на основі розгорток.

 

 

 

 

ВИСНОВКИ

Сучасний тренд «STEM-освіта» – концепція інтегрованого навчання здобувачів освіти за чотирма профільними дисциплінами в міждисциплінарному та прикладному контексті є надзвичайно актуальним феноменом в аспекті стратегічного розвитку провідних країн світу щодо отримання ними конкурентних переваг у різних сферах людської діяльності. Саме STEM-освіта сприяє підготовці компетентних фахівців для високотехнологічних виробництв і забезпечує високий науковий потенціал будь-якої держави.

STEM-освіта є мостом, що об’єднує навчання та кар’єру. Його концепція готує дітей до технологічно розвинутого світу. Спеціалістам майбутнього потрібні всебічна підготовка та знання з самих різних навчальних областей природничих наук, інженерії, технології, математики тощо.

STEM-освіта сьогодні демонструє потужний науковий потенціал, для реалізації якого потрібно розробити стандарти STEM-орієнтованого освітнього контенту. Це можливо лише спільними зусиллями всіх учасників освітнього процесу, використовуючи інновації, передові комп’ютерні технології. Об’єднавши зусилля освітніх закладів, наукових установ та державних органів у поширенні здобутків у галузі STEM-освіти, необхідно впроваджувати елементи STEM у всі заклади освіти.

Підсумовуючи вище викладене, варто зазначити, що в сучасній соціокультурній ситуації інтенсивно формується нове уявлення щодо перспектив подальшого розвитку системи української освіти, надання якісних освітніх послуг, зокрема через упровадження в закладах освіти моделі STEM. Системний підхід до вивчення природничо-математичних дисциплін, на якому базується STEM-навчання, сприяє розвитку інновацій, реалізації творчого потенціалу особистості та її допрофесійної підготовки.

Заклади позашкільної освіти активно долучаються до процесів упровадження STEM-освітньої моделі: упровадження інтегрованого підходу до навчання вихованців, розвитку навичок критичного мислення, активної комунікації і командної роботи, підготовки дітей до технологічних інновацій життя, застосування науково-технічних знань у реальному житті.

Отже, є всі підстави вважати, що STEM-освіта здатна стати тим фактором, що значно підвищить якість позашкільної освіти в аспекті підготовлення майбутніх фахівців. Залучення дітей до SТЕМ-освіти, вибору ними подальших занять у закладах освіти, набуття навичок за інтересами дає змогу профорієнтувати гуртківців до професій, які пов’язані з технікою та наукою.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток А

Схеми для танграма

 

 

 

Додаток Б

Шаблони для конструктора з картону

 

 

 

 

 

 

 

 

 

 

 

 Додаток В

Додаток Г

 

Додаток Д

 

 

 

 

Додаток Е

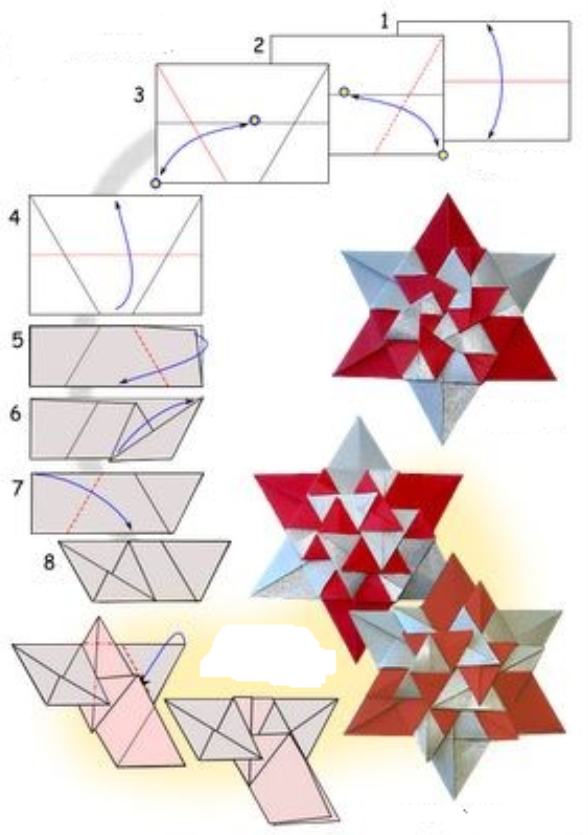
Виготовлення тригексафлексагона

Постійні моделі були названі гексафлексагонами: «гекса» - тому що шестикутна форма, «флексагонами» - через властивість складатися. Перший виготовлений Стоуном флексагон був названий тригексафлексагоном, так як у нього були три поверхні.

 

 

Інструкція

Щоб не заплутатись при складанні тригексафлексагона: лицева сторона — біла, зворотня — сіра.

1.                   Вирізаємо шаблон (або креслимо 10 рівносторонніх трикутників). Надписуємо цифри або розмальовуємо.
2.                   Зігнути по всіх пунктирних лініях і знову розігнути.
3.                    

 

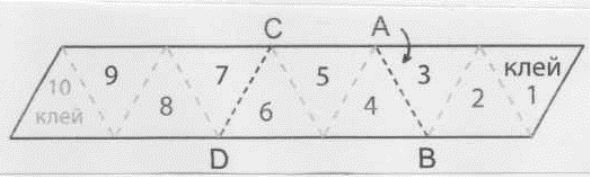
4.                   Зігнути по лінії АВ, відігнувши 3 трикутники (1-3) вперед.

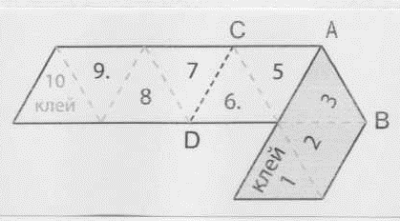
5.                   Зігнути по лінії CD, відігнувши з другої сторони 4 трикутники (7-10) назад.

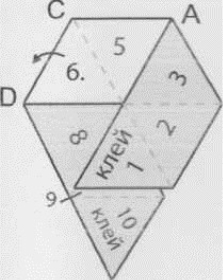
6.                   Підсунути кутик 1 вниз під 9, відігнути кутик 10 вниз і склеїти 10 з 1 лицевими сторонами.

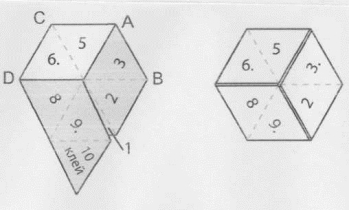
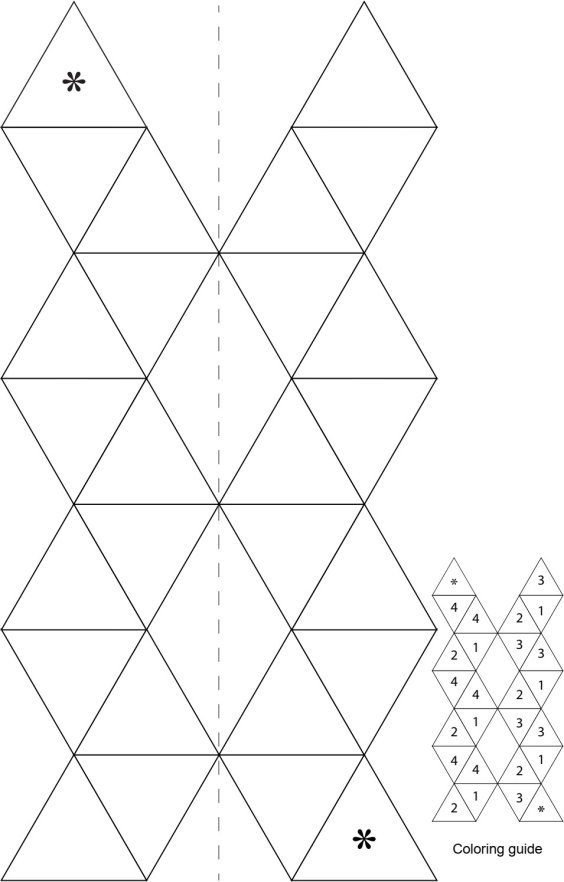
Виготовлення тетрагексафлексагона

Тетрафлексагон також існує лише в єдиному варіанті. Його складають із «пилкоподібної» смужки і має чотири поверхні.

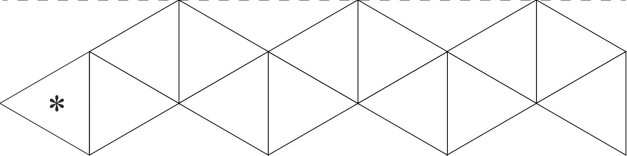
1. Підготувати смужку паперу, поділену на 13 рівносторонніх трикутників ( можна роздрукувати шаблон)

Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався. Прономерувати трикутники з однієї сторони цифрами 3,1,2,3 (за зразком)

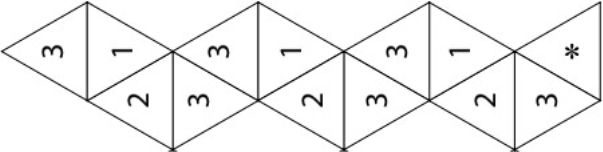
Перевернути цю смужку і пронумерувати трикутники на зворотній стороні цифрами 4,4,1,2. * – позначено трикутник який буде склеюватись.

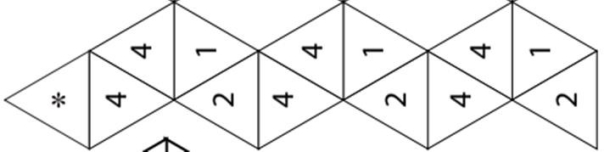
2. Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери (з цифрами 4) опинились накладені один на одного.

3. Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 1) опинились накладені один на одного.

4. Залишається лише підігнути кутик з зірочкою вниз і приклеїти його до іншого трикутника з зірочкою на нижній стороні смужки. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 3, а на всіх трикутниках на зворотній стороні – цифра 2.

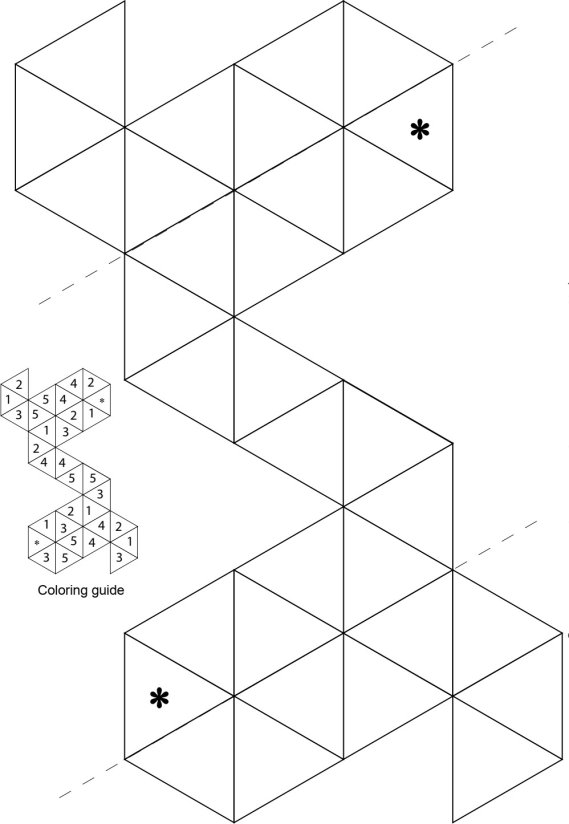
Виготовлення пентагексафлексагона

Пантофлексагон має п’ять поверхней. Єдиний різновид цього флексагона складають зі смужки, що зображена на малюнку.

1.    Підготувати смужку паперу, розподілену на 16 рівносторонніх трикутників ( можна роздрукувати шаблон).
2. Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3.         Прономерувати трикутники з однієї сторони цифрами 1,2,3,1,2,4,4,5,5,3,1,2,3,1

Перевернути цю смужку і прономерувати трикутники на зворотній стороні цифрами 3,5,5,4,4,2,1,3,2,1,3,5,5,4,4,2.

4.    Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери (з цифрами 5) опинились накладені один на одного. В результаті вийде              ось така смужка.

5.                        Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 4) опинились накладені один на одного.

6.                        Скласти смужку так, щоб трикутники, які мають одинакові номери (з цифрами 3) опинились накладені один на одного.

7. Залишається лише підігнути трикутник з зірочкою вниз і приклеїти його до іншого трикутника з зірочкою на нижній стороні смужки. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні цифра 2.

Згинаючи   гексагексафлексагон,   можна   побачити  всі  п’ять його  поверхней.

Виготовлення гептагексафлексагона.

Інший, на менш цікавий флексагон отримав назву гептагексафлексагон ( перше «гепта» - сім- це значить кількість поверхонь цієї моделі) .

1.    Підготувати смужку паперу, розподілену на 22 рівносторонніх трикутників ( можна роздрукувати шаблон).
2. Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3.       Пронумерувати трикутники з однієї сторони цифрами 1,2,3,1,2,7,7,6,4,4,5,5,6,3,1,2,3,1,2,7,7,6

 

Перевернути цю смужку і пронумерувати трикутники на зворотній стороні цифрами х,4,4,5,5,6,3,1,2,3,1,2,7,7,6,4,4,5,5,6,3,х, де х- місце нанесення клею.

 

 

Як варіант, можна замість цифр розфарбувати в різні кольори ( кожній цифрі відповідає тільки один колір)

4.       Скласти смужку так, щоб трикутники зі зворотньої сторони, які мають одинакові номери опинились накладені один на одного. Починаємо з цифри 7, а потім – 6 і т. д.

 

Згинаючи гексагексафлексагон, можна побачити всі сім його поверхонь. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні – цифра 2.

 

 

Виготовлення гексагексафлексагона.

Інший, на менш цікавий флексагон отримав назву гексагексафлексагон ( перше «гекса» - шість- це значить кількість поверхонь цієї моделі) .

1. Підготувати смужку паперу, розподілену на 19 рівносторонніх трикутників ( можна роздрукувати шаблон)
2.                   Зробити згини кожної лінії, які ділять смужку на трикутники в обидві сторони, щоб майбутній флексагон легко розкривався.
3.       Пронумерувати трикутники з однієї сторони цифрами 1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3.

Перевернути цю смужку і пронумерувати трикутники на зворотній стороні цифрами 4,4,5,5,6,6,4,4,5,5,6,6,4,4,5,5,6,6.

 

Як варіант можна замість цифр розфарбувати в різні кольори ( кожній цифрі відповідає тільки один колір) чи намалювати на них будь-яку геометричну фігуру.

4.                   Скласти смужку так, щоб трикутники зі зворотної сторони, які мають одинакові номери опинились накладені один на одного. В результаті вийде ось така смужка.

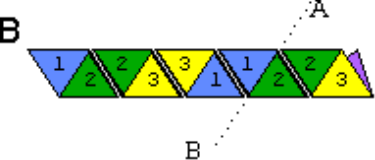
5. Зігнути по лінії аб, відігнувши 3 трикутники (3,2,2) вперед.
6. Зігнути по лінії сд, відігнувши з другої сторони 4 трикутники (1,1,3 і не пронумерований) назад.

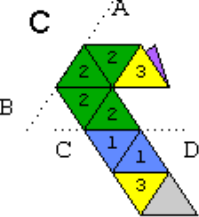
7. Залишається лише підігнути не пронумерований трикутник вниз і приклеїти його до не пронумерованого трикутника на нижній стороні смужки.

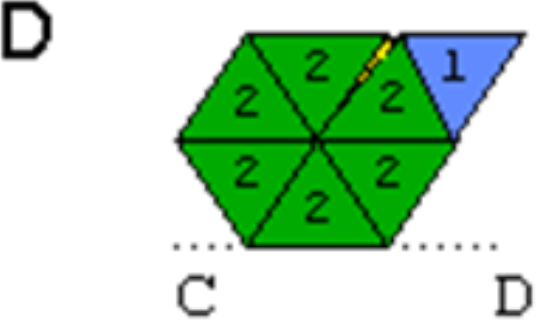
Згинаючи гексагексафлексагон, можна побачити всі шість його поверхонь. Для цієї моделі сторони з цифрами 1, 2 і 3 будуть з’являтися частіше, ніж 4, 5 і 6. Виконати всі дії значно легше ніж описати. Якщо все виконано вірно, то на всіх трикутниках видимої сторони шестикутника повинна стояти цифра 1, а на всіх трикутниках на зворотній стороні – цифра 2.

 

 

 

 

 

Додаток Є

Інструкція виготовлення  флексорів

1. Розфарбувати шаблон, вирізати.

2. Зробити лінії згину по вертикалі і діагоналі, добре загладити.

3. Вийде складена «трубка».

4. Склеїти (клеєм або двостороннім скотчем).

5. Скласти модель в коло і склеїти.

6. Робота завершена.

 

 

 

 

Додаток Ж

 

Шаблон тригексафлексагона

 

 

 

Шаблон тетрагексафлексагона

Шаблон пентагексафлексагона

Шаблони шестикутного флексора

Шаблони восьмикутного флексора

 

 

 

 

 

 

 

 

 

Додаток З

 

 

Додаток К

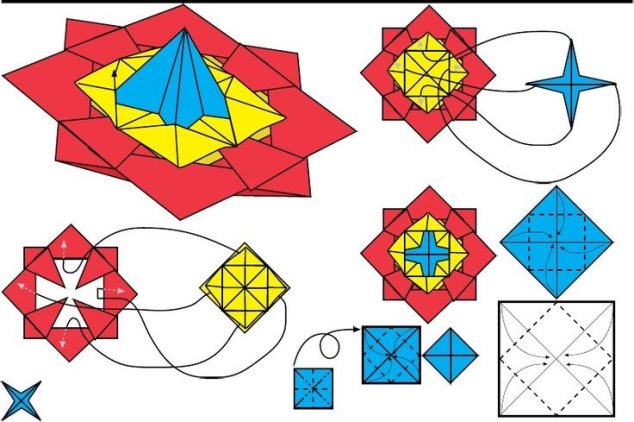
Виготовлення об’ємних фігур в техніці оригамі

 

 

 

 

Багатокутник

 

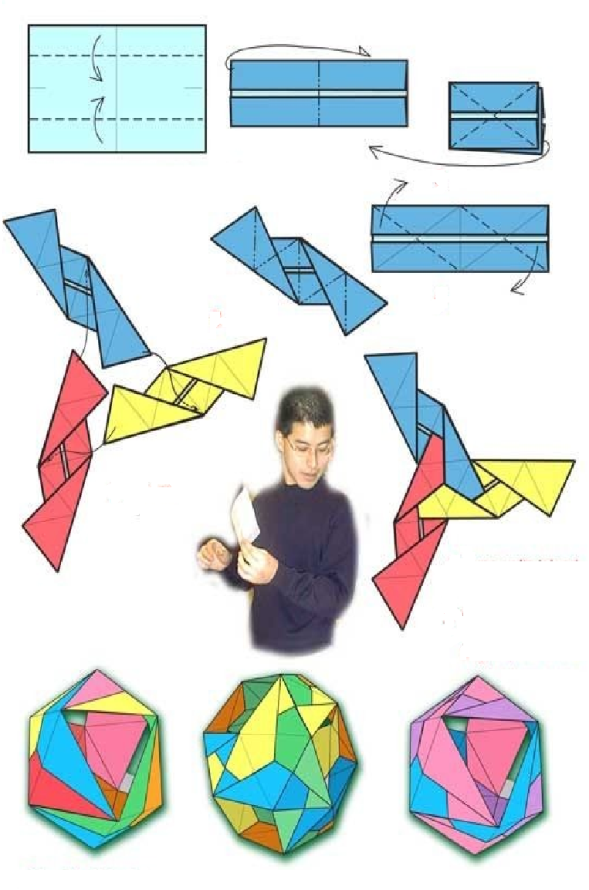
Куб (Варіант 1)

 

 

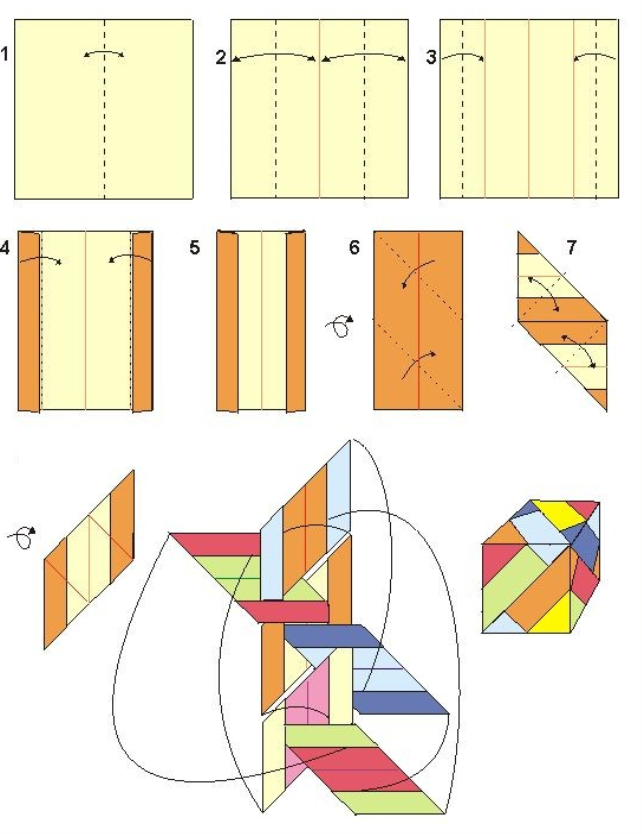
 Куб (Варіант 2)

 

 

 

 

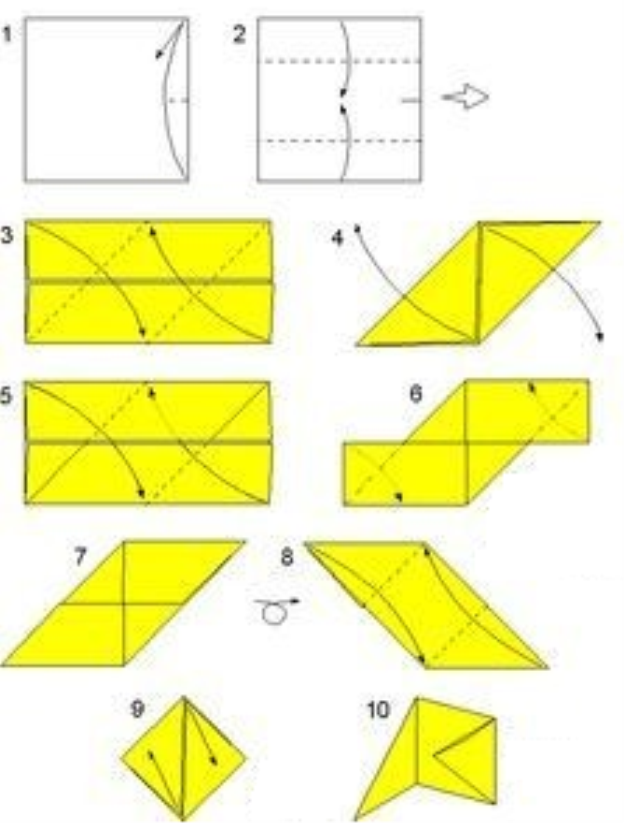
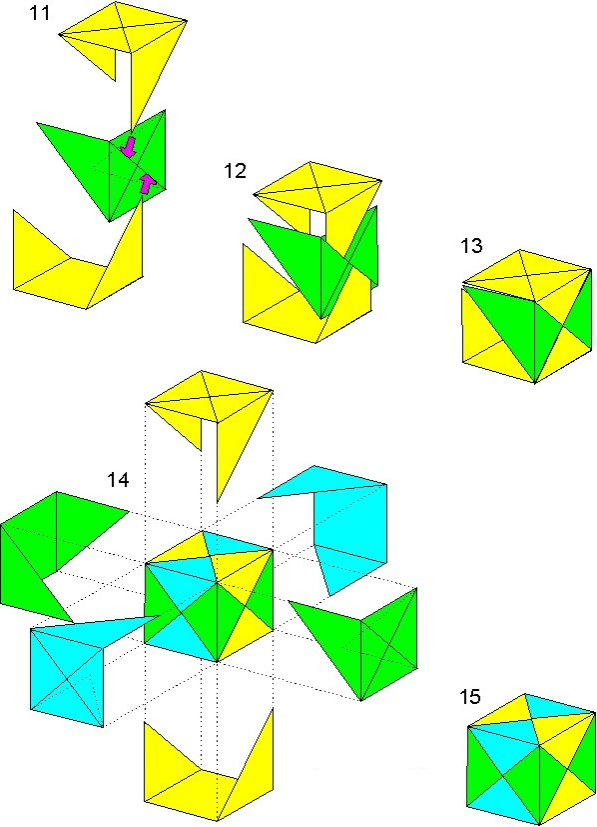
Додаток Л

 

Додаток М

 

 

 

 

 

 

 

Додаток Н

 

 

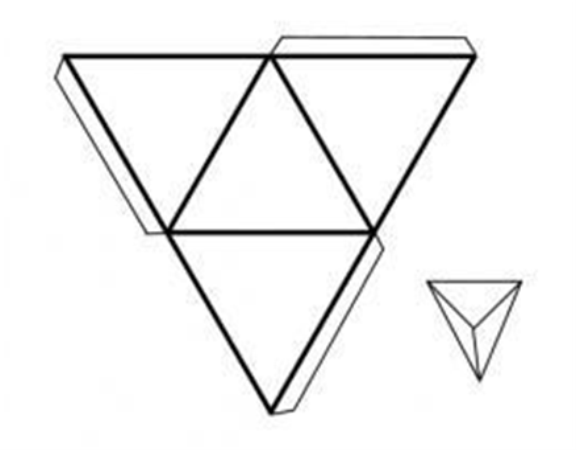
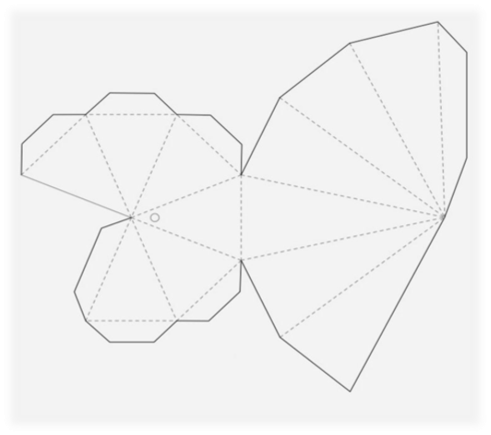
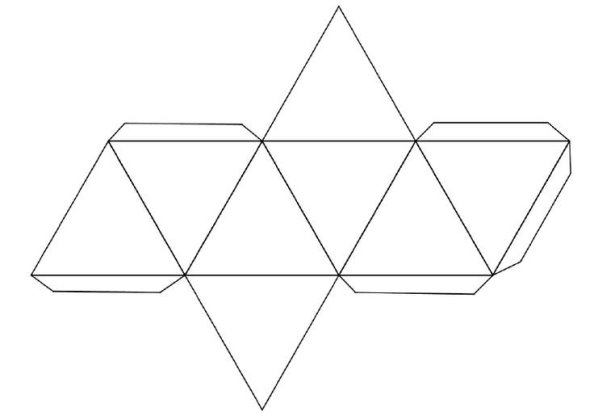
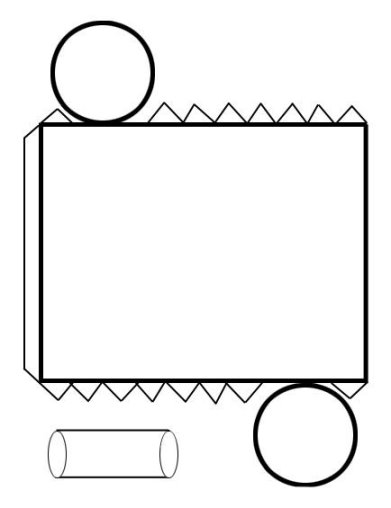
Додаток О

Розгортки об’ємних фігур (форми)

 

 

 

 

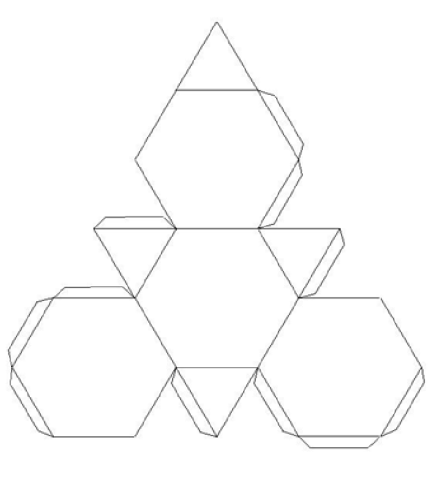
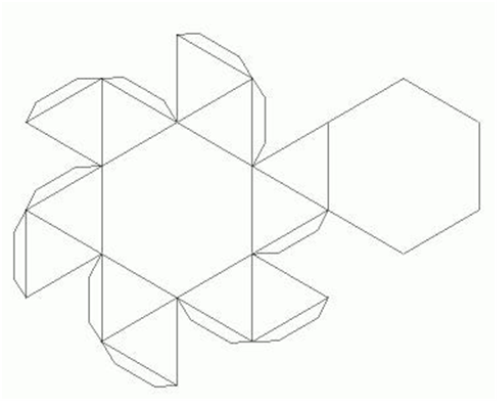
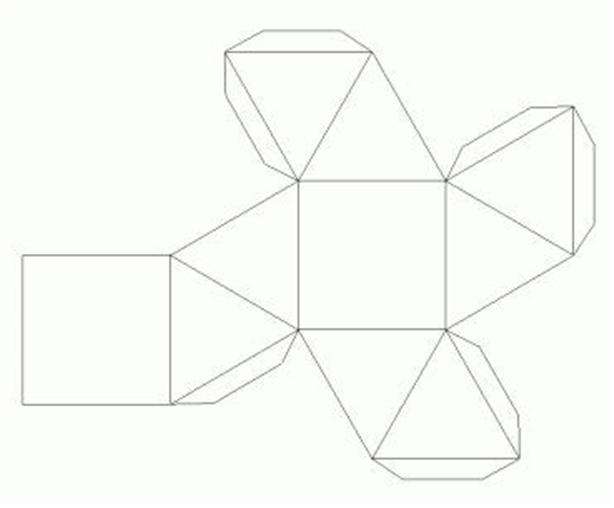
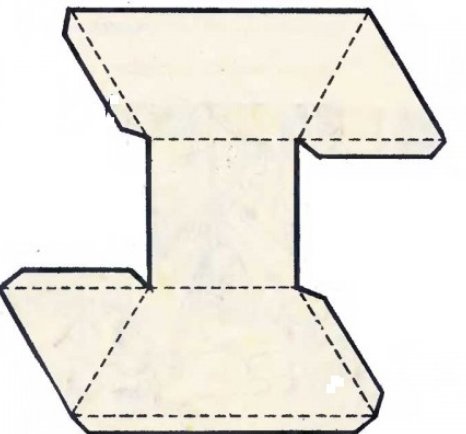
Використана література

1.          Мартинюк І. Творчий потенціал і самореалізація особистості /І. Мартинюк // Психологія і педагогіка життєтворчості. – К.,1996. – 792 с.
2.          Доценко С.О. Прийоми активізації творчої діяльності учнів в умовах STEM-освіти/ Доценко С.О.//Професійна освіта: методологія, теорія та технології. – 2016. – №4. – С. 32-44.
3.          Доценко С.О., Лебедева В.В. STEM-освіта як засіб активізації творчого потенціалу особистості [Електронний ресурс]/Харківський національний педагогічний університет ім. Григорія Сковороди. – м. Харків. – Режим доступу:

http://www.dgma.donetsk.ua/docs/konf/2017/mkonf2017/dopovidy/it

4.          Савченко І., Савченко Я., STEM-освіта як ключовий фактор формування критичної особистості юного дослідника/ [редкол.С.О. Довгий (голова), О.Є. Стрижак, І.М. Савченко (відп. ред.) та ін.].// Наукові записки Малої академії наук України. – Вип. 10. – Серія : Педагогічні науки : зб. наук. пр – К., 2017. – №10. – С. 47-59.